12 Derivadas de funciones de varias variables

Hasta ahora hemos estado estudiando funciones que dependían de una sola variable independiente, pero en muchos casos de la vida real aparecen funciones que dependen de más de una variable, como por ejemplo

El área de un triángulo depende de dos factores que son su base y su altura.
El volumen que ocupa un gas perfecto depende de dos factores que son su presión y su temperatura.
El capital de una inversión depende de el tiempo y el tipo de interés.
El camino recorrido por un cuerpo en un movimiento de caída libre depende de multitud de factores entre los que cabe destacar: el tiempo que dure la caída, el área de la sección transversal del cuerpo, la latitud del lugar, la altura sobre el nivel del mar, la presión del aire, la temperatura del aire, etc.

Estas dependencias se expresan con funciones de varias variables. En este capítulo analizaremos las derivadas este tipo de funciones, en particular funciones de $\mathbb{R}^2$ en $\mathbb{R}$ y de $\mathbb{R}^3$ en $\mathbb{R}$, aunque los resultados se pueden generalizar fácilmente para funciones de $\mathbb{R}^n$ en $\mathbb{R}$.

12.1 Función de varias variables

Definición 12.1 (Función de varias variables) Una función de $n$ variables de un conjunto $A_1\times \cdots \times A_n$ en un conjunto $B$, es una relación que asocia a cada tupla $(a_1,\ldots,a_n)\in A_1\times \cdots\times A_n$ un único elemento de $B$ que se denota $f(a_1,\ldots,a_n)$, y se llama imagen de $(a_1,\ldots,a_n)$ mediante $f$.

\[ \begin{array}{lccc} f: & A_1\times\cdots\times A_n & \longrightarrow & B \\ &(a_1,\ldots,a_n) & \longrightarrow & f(a_1,\ldots,a_n) \end{array} \]

Cuando $A_1,\ldots,A_n,B\subseteq \mathbb{R}$, entonces se dice que $f$ es una función real de $n$ variables reales o bien un campo escalar.

Ejemplo 12.1

El área de un triángulo es la función real de dos variables reales

\[f(x,y)=\frac{xy}{2}.\]

El volumen de un gas perfecto es otra función real de dos variables

\[v=f(t,p)=\frac{nRt}{p},\]

con $n$ y $R$ constantes.

12.1.1 Gráfica de una función de dos variables

La representación gráfica cartesiana de una función de dos variables $f(x,y)$ es una superficie del espacio real $\mathbb{R}^3$ donde cada punto de la superficie tiene coordenadas $(x,y,z)$, siendo $z=f(x,y)$.

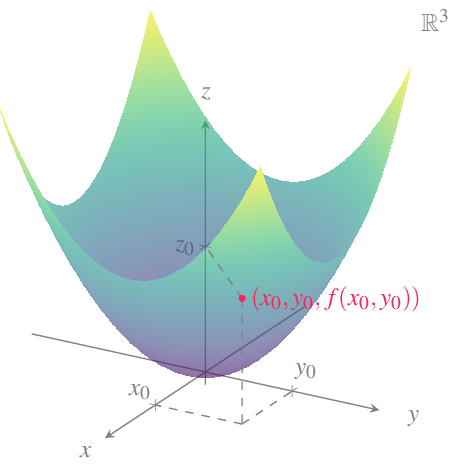
Representación gráfica de una función de dos variables.

Ejemplo 12.2 La función $f(x,y)=\dfrac{xy}{2}$ que mide el área de un triángulo de base $x$ y altura $y$ tiene la siguiente representación gráfica:

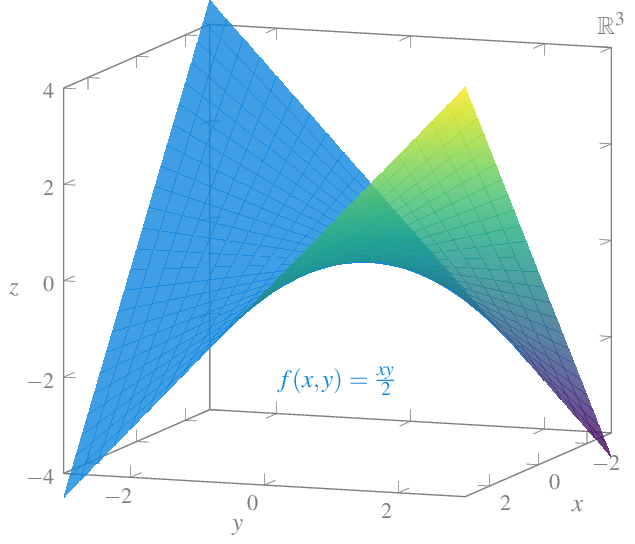
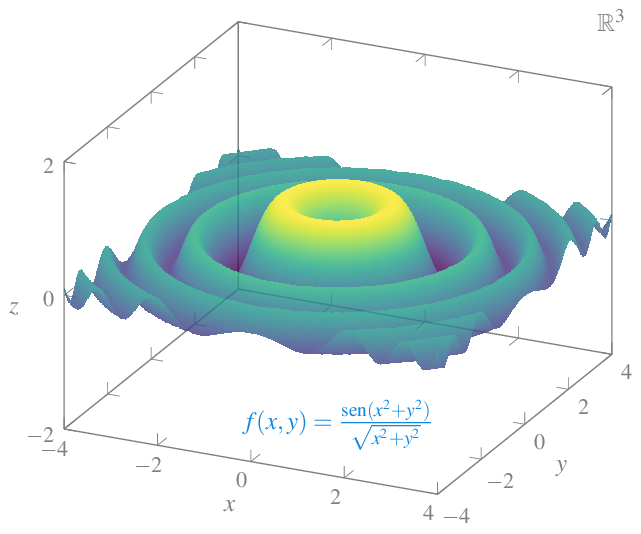
Gráfica de la función que mide el área de un triángulo.

Y la función $\displaystyle f(x,y)=\frac{\operatorname{sen}(x^2+y^2)}{\sqrt{x^2+y^2}}$ tiene la siguiente representación gráfica que simula las ondas que produce una gota de agua al caer sobre un líquido.

Gráfica de la función que representa las ondas creadas por una gota de agua.

12.1.2 Conjunto de nivel de una función de varias variables

Visualizar la gráfica de una función de dos variables no es fácil, sobre todo si se representa en un papel que, a fin de cuentas, es un plano en dos dimensiones. Un recurso bastante habitual para entender el comportamiento de una función de dos variables son las curvas de nivel, que consisten en representar en el plano euclídeo los puntos $(x,y)$ que tienen la misma imagen.

Definición 12.2 (Conjunto de nivel) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, se llama conjunto de nivel $c$ de $f$ al conjunto

\[ C_{f,c}=\{(x_1,\ldots,x_n): f(x_1,\ldots,x_n)=c\}. \]

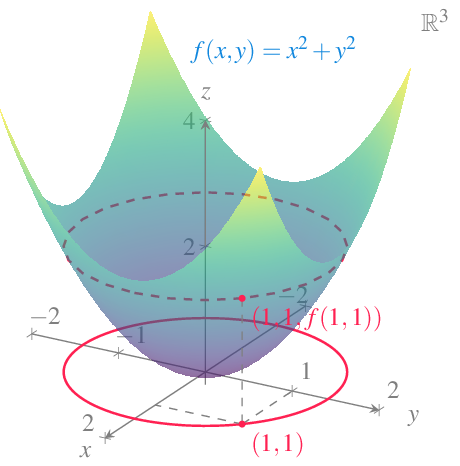
Ejemplo 12.3 Si $f(x,y)=x^2+y^2$ y $P=(1,1)$, el conjunto de nivel de $f$ que incluye al punto $P$ es

\[ C_{f,2} = \{(x,y): f(x,y)=f(1,1)=2\} = \{(x,y): x^2+y^2=2\}, \]

que es la circunferencia del plano real centrada en el origen y de radio $\sqrt{2}$.

Gráfica del conjunto de nivel de un paraboloide.

:::{#exm-curvas-nivel} La siguiente gráfica representa algunas de las curvas de nivel de la función $f(x,y) = y^2-x^2$.

Gráfica y curvas de nivel de la función $f(x,y) = y^2-x^2$.

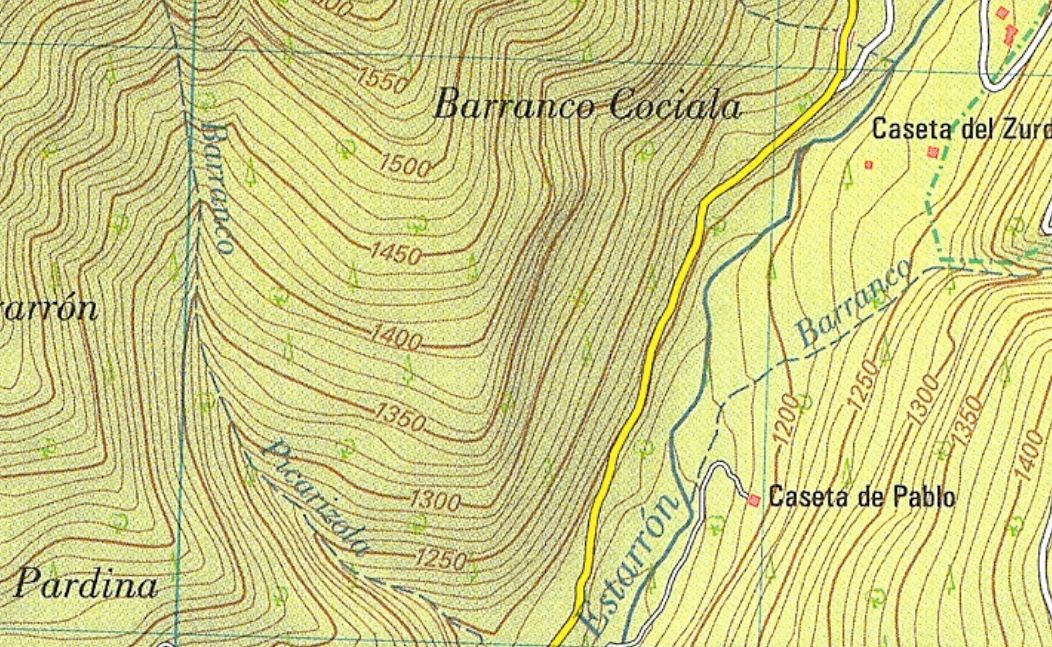
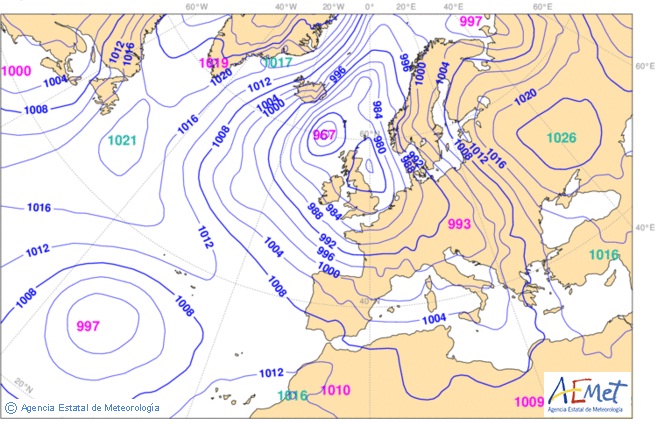
Las curvas de nivel se utilizan en muchas aplicaciones como por ejemplo en los mapas topográficos, donde cada curva representa los puntos que están a la misma altura sobre el nivel del mar, o en los mapas meteorológicos, donde cada curva representa los puntos con la misma presión atmosférica.

Curvas de nivel de un mapa de presión atmosférica.

12.2 Límites de funciones de varias variables

El concepto de límite de una función de una variable se puede extender fácilmente a funciones de varias variables, pero antes necesitamos introducir, desde un punto de vista topológico, el concepto equivalente a un entorno de un punto en la recta real, en espacios de mayor dimensión.

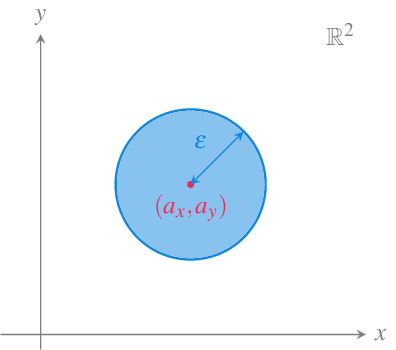
Definición 12.3 (Entorno de un punto en el plano real) Dado un punto del plano $(a_x,a_y)\in \mathbb{R}^2$, se llama entorno de $(x_0,y_0)$ a cualquier disco abierto $\{(x,y):|(x,y)-(a_x,a_y)|<\varepsilon\}$ con $\varepsilon>0$. El número $\varepsilon$ se conoce como radio del entorno.

Para cualquier $\varepsilon>0$ el conjunto $\{(x,y):|(x,y)-(a_x,a_y)|<\varepsilon\}\setminus \{(a_x,a_y)\}$ se llama entorno reducido de $(a_x,a_y)$.

Geométricamente, un entorno de $(a_x,a_y)$ de radio $\varepsilon$ está formado por todos los puntos interiores del círculo de radio $\varepsilon$ centrado en $(a_x,a_y)$.

De manera similar se define un entorno en el espacio real.

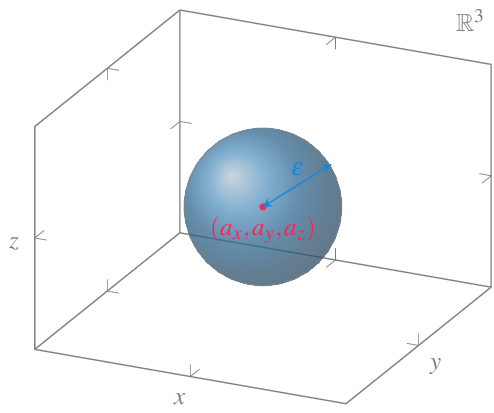
Definición 12.4 (Entorno de un punto en el espacio real) Dado un punto del espacio $(a_x,a_y,a_z)\in \mathbb{R}^3$, se llama entorno de $(a_x,a_y,a_z)$ a cualquier bola abierta $\{(x,y,z):|(x,y,z)-(a_x,a_y,a_z)|<\varepsilon\}$ con $\varepsilon>0$. El número $\varepsilon$ se conoce como radio del entorno.

Para cualquier $\varepsilon>0$ el conjunto $\{(x,y,z):|(x,y,z)-(a_x,a_y,a_z)|<\varepsilon\}\setminus \{(x_0,y_0,z_0)\}$ se llama entorno reducido de $(a_x,a_y,a_z)$.

Geométricamente, un entorno de $(a_x,a_y,a_z)$ de radio $\varepsilon$ está formado por todos los puntos interiores de la esfera de radio $\varepsilon$ centrado en $(a_x,a_y,a_z)$.

Definición 12.5 (Límite de una función de varias variables) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$ definida en un entorno reducido del punto $(a_1, \ldots, a_n)$, se dice que $l$ es el límite de $f$ en el punto $(a_1, \ldots, a_n)$, si para cada $\varepsilon>0$ existe un $\delta>0$ tal que si $0<|(x_1,\ldots,x_n)-(a_1,\ldots,a_n)|<\delta$, entonces $|f(x_1,\ldots,x_n)-l|<\varepsilon$, y en tal caso, se denota

\[ \lim_{(x_1,\ldots,x_n)\rightarrow (a_1,\ldots,a_n)}f(x_1,\ldots,x_n) = l. \]

Ejemplo 12.4 Veamos que el límite de la función $f(x,y)=\frac{2xy^2}{x^2+y^2}$ en $(0,0)$ es $0$.

Dado $\varepsilon>0$, como

\[\begin{align*} |f(x,y)-0| &= \left|\frac{2xy^2}{x^2+y^2}\right| = |2x|\left|\frac{y^2}{x^2+y^2}\right| \\ & \leq 2|x| = 2\sqrt{x^2} \leq 2\sqrt{x^2+y^2} \\ &= 2|(x,y)-(0,0)| \end{align*}\]

Por tanto, si tomamos $\delta = \epsilon/2$, se tiene que si $|(x,y)-(0,0)|<\delta = \epsilon/2$, entonces

\[ |f(x,y)-0| \leq 2|(x,y)-(0,0)| < 2\frac{\varepsilon}{2} = \varepsilon. \]

En el caso de una función de una variable $f(x)$, vimos que para que existiese el límite de la función en el punto $a$, bastaba con ver que existía el límite por la izquierda (cuando nos aproximamos a $a$ con valores menores que $a$) y el límite por la derecha (cuando nos aproximamos a $a$ con valores mayores que $a$) y que eran iguales. Sin embargo, para funciones de varias variables esto no es así, ya que para demostrar la existencia del límite es necesario probar que el límite existe cuando nos acercamos a $(x_0,\ldots,y_0)$ por cualquier posible trayectoria en $\mathbb{R}^n$, y todos los límites coinciden.

Ejemplo 12.5 El límite de la función $f(x,y)=\dfrac{xy}{x^2+y^2}$ en $(0,0)$ no existe, ya que si nos aproximamos a $(0,0)$ tomando puntos de la recta $y=mx$, tenemos

\[\begin{align*} \lim_{(x,mx)\to(0,0)} f(x,mx) &= \lim_{x\to 0} \frac{xmx}{x^2+(mx)^2} = \lim_{x\to 0} \frac{mx^2}{(m^2+1)x^2} \\ & \lim_{x\to 0} \frac{m}{m^2+1} = \frac{3m}{m^2+1}, \end{align*}\]

que nos da un límite distinto para cada $m$, es decir, para cada dirección de aproximación obtenemos un límite distinto.

Precaución

La estrategia de calcular el límite a lo largo de las trayectorias rectas $y=y_0+m(x-x0)$ que pasan por el punto $(x_0,y_0)$ no garantiza la existencia del límite, aún cuando todos los límites existan y sean iguales.

Ejemplo 12.6 Para la función $f(x,y)=\frac{xy^2}{x^2+y^4}$, si nos aproximamos a $(0,0)$ tomando los puntos de la recta $y=mx$, se tiene

\[ \lim_{(x,mx)\to(0,0)} f(x,mx) = \lim_{x\to 0} \frac{x(mx)^2}{x^2+(mx)^4} = \lim_{x\to 0} \frac{m^2x}{1+m^4x^2} = 0. \]

Por tanto, el límite existe y vale $0$ cuando nos aproximamos a $(0,0)$ siguiendo trayectorias rectas. Sin embargo, existen otras trayectorias de aproximación donde el límite no existe, como por ejemplo, la trayectoria $y = \sqrt{x}$.

\[ \lim_{(x,\sqrt{x})\to(0,0)} f(x,\sqrt{x}) = \lim_{x\to 0} \frac{x(\sqrt{x})^2}{x^2+(\sqrt{x})^4} = \lim_{x\to 0} \frac{x^2}{2x^2} = \frac{1}{2}. \]

Por consiguiente, no existe el límite de $f$ en $(0,0)$.

Figura 12.1: Función de dos variables sin límite en $(0,0)$.

Afortunadamente, el álgebra de límites visto en la Proposición 6.2 también es válido para funciones de varias variables.

Ejemplo 12.7 El límite de la función $f(x,y)=\frac{3xy^2}{x^2+y^3}$ en el punto $(2,1)$ es

\[\begin{align*} \lim_{(x,y)\to(2,1)} f(x,y) &= \lim_{(x,y)\to(2,1)} \frac{3xy^2}{x^2+y^3} \\ &= \frac{\lim_{(x,y)\to(2,1)} 3xy^2}{\lim_{(x,y)\to(2,1)} x^2+y^3} \\ &= \frac{3\lim_{(x,y)\to(2,1)} x\lim_{(x,y)\to(2,1)}y^2}{\lim_{(x,y)\to(2,1)} x^2+\lim_{(x,y)\to(2,1)}y^3} \\ &= \frac{3\cdot 2\cdot 1^2}{2^2 + 1^3} = \frac{6}{5}. \end{align*}\]

12.3 Continuidad de funciones de varias variables

Una vez definido el límite de una función de varias variables, el concepto de continuidad se extiende de manera natural a funciones de varias variables.

Definición 12.6 Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, se dice que $f$ es continua en el punto $(a_1, \ldots, a_n)$ si

\[ \lim_{(x_1,\ldots,x_n)\rightarrow (a_1,\ldots,a_n)}f(x_1,\ldots,x_n) = f(a_1,\ldots, a_n). \]

Ejercicio 12.1 Hemos visto en el Ejemplo 12.4 que el límite de la función $f(x,y)=\frac{2xy^2}{x^2+y^2}$ en $(0,0)$ es $0$. Sin embargo, esta función no está definida en $(0,0)$, por lo que es discontinua en este punto.

12.3.1 Funciones parciales

Definición 12.7 (Función parcial) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, se llama función parcial $i$-esima de $f$ a cualquier función $f_i:\mathbb{R}\rightarrow \mathbb{R}$ que resulta de fijar todas las variables de $f$ como constantes, excepto la variable $i$, es decir:

\[f_i(x)=f(c_1,\ldots,c_{i-1},x,c_{i+1},\ldots,c_{n}),\]

con $c_j$ $(j=1,\ldots, n,\ j\neq i)$ constantes.

Ejemplo 12.8 Si consideramos la función del área de un triángulo

\[f(x,y)=\frac{xy}{2},\]

y fijamos el valor de la base $x=c$, entonces el área del triángulo ya sólo depende de la altura y $f$ se convierte en una función de una sola variable, que es la función parcial:

\[ f_1(y)=f(c,y)=\frac{cy}{2}, \]

con $c$ constante.

12.4 Derivadas parciales

Al igual que vimos cómo calcular la variación de una función de una variable, tiene sentido medir la variación de una función de varias variables con respecto a cada una de sus variables.

Sea $f(x,y)$ una función de varias variables en $\mathbb{R}^2$. Si estamos en el punto $(a,b)$ y nos movemos una cantidad $\Delta x$ en la dirección del eje $X$, entonces, al mantenerse la coordenada $y$ constante, pasaremos desde el punto $(a,b)$ al punto $(a+\Delta x,b)$, y la variación que experimenta la función será

\[ \Delta z=f(a+\Delta x,b)-f(a,b). \]

La variación relativa que experimenta la función con respecto a la variable $x$ vendrá dada por el cociente

\[ \frac{\Delta z}{\Delta x}=\frac{f(a+\Delta x,b)-f(a,b)}{\Delta x}. \]

Si en lugar de medir la variación de una función con respecto a una variable en un intervalo, medimos la variación en un punto, es decir, cuando $\Delta x$ tiende a 0, entonces obtenemos una tasa de variación instantánea:

\[ \lim_{\Delta x\rightarrow 0}\frac{\Delta z}{\Delta x}=\lim_{\Delta x \rightarrow 0}\frac{f(a+\Delta x,b)-f(a,b)}{\Delta x}. \]

Al valor del límite, cuando existe, también se le conoce como derivada parcial de $f$ con respecto a la variable $x$ en el punto $(a,b)$, y mide la tasa de variación instantánea de $f$ en el punto $(a,b)$ cuando el punto se mueve en la dirección del eje $X$.

Del mismo modo, si estamos en el punto $(a,b)$ y nos movemos una cantidad $\Delta y$ en la dirección del eje $Y$, manteniendo la coordenada $x$ constante, pasaremos desde el punto $(a,b)$ al punto $(a,b+\Delta y)$, y la tasa de variación instantánea de la función en ese punto viene dada por el límite

\[ \lim_{\Delta y\rightarrow 0}\frac{\Delta z}{\Delta y}=\lim_{\Delta y \rightarrow 0}\frac{f(a,b+\Delta y)-f(a,b)}{\Delta y}, \]

que cuando existe se conoce como derivada parcial de $f$ con respecto a la variable $y$ en el punto $(a,b)$, y mide la tasa de variación instantánea de $f$ en el punto $(a,b)$ cuando el punto se mueve en la dirección del eje $Y$.

El concepto de derivada parcial puede extenderse fácilmente para funciones de $n$ variables.

Definición 12.8 (Derivada parcial) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, se dice que $f$ es derivable parcialmente con respecto a la variable $x_i$ en el punto $a=(a_1,\ldots,a_n)$ si existe el límite

\[ \lim_{h\rightarrow 0} \frac{f(a_1,\ldots,a_{i-1},a_i+h,a_{i+1},\ldots,a_n)-f(a_1,\ldots,a_{i-1},a_i,a_{i+1},\ldots,a_n)} {h}. \]

En tal caso, al valor del límite se le llama derivada parcial de $f$ en $a$ con respecto a la variable $x_i$, y se denota

\[ f'_{x_i}(a)=\frac{\partial f}{\partial x_i}(a). \]

12.4.1 Interpretación geométrica de la derivada parcial

Geométricamente, $z=f(x,y)$ define una superficie. Si se corta esta superficie con el plano de ecuación $y=b$ (es decir, si $y$ se fija como una constante), la intersección de este plano con la superficie es una curva plana cuya pendiente en el punto $(a,b)$ es la derivada parcial de $f$ con respecto a $x$ en el punto $(a,b)$.

Ejemplo interactivo con Geogebra

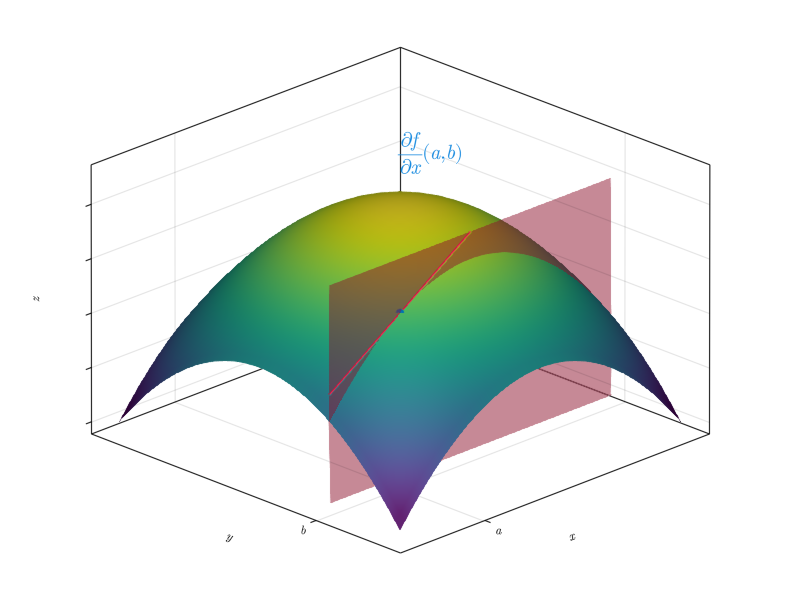
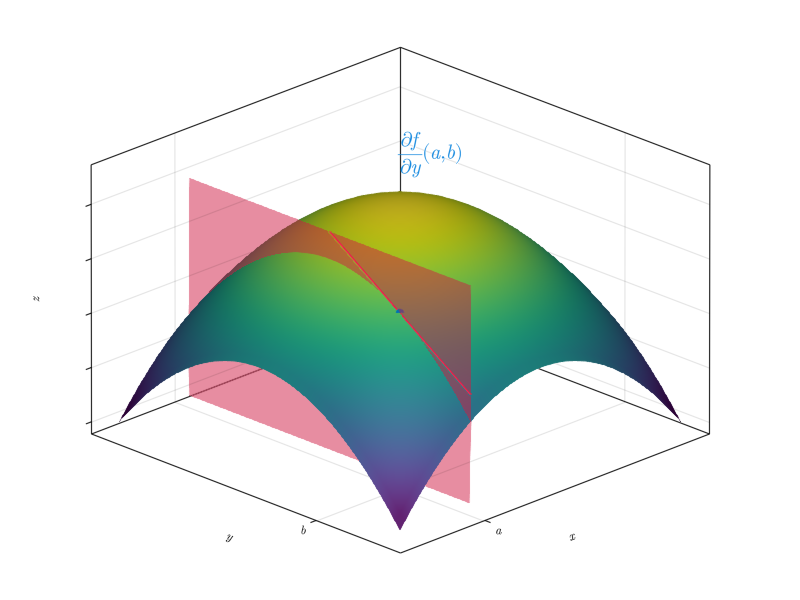
Como se puede observar, la definición de derivada para funciones de una variable es un caso particular de esta definición para $n=1$.

Al medir la variación de $f$ con respecto a la variación de una sola de sus variables $x_i$ en un punto $a=(a_1,\ldots,a_n)$, el resto de las variables se pueden considerar como constantes y, en tal caso, podemos ver a $f$ como una función parcial $i$-ésima

\[ f_i(x_i)=f(a_1,\ldots,a_{i-1},x_i,a_{i+1},\ldots,a_n). \]

La derivada parcial de $f$ con respecto a $x_i$ puede calcularse derivando esta función:

\[ \frac{\partial f}{\partial x_i}(a)=f_i'(a_i). \]

Regla

Para derivar parcialmente $f(x_1,\ldots,x_n)$ con respecto a una variable $x_i$, se deriva $f$ como si la única variable fuese $x_i$, tratando el resto de las variables como constantes.

Ejemplo 12.9 En la ecuación de estado de los gases perfectos, el volumen es una función que depende de dos variables

\[ v(t,p)=\frac{nRt}{p}, \]

donde $t$ mide la temperatura, $p$ la presión y $n$ y $R$ son constantes.

La tasa de variación instantánea que experimenta el volumen con respecto a la presión viene dada por la derivada parcial de $v$ con respecto a $p$.

Para calcular esta derivada parcial se fija $t$ como constante y se deriva $v$ como si la única variable fuese $p$:

\[ \frac{\partial v}{\partial p}(t,p)=\frac{d}{dp}\left(\frac{nRt}{p}\right)_{\mbox{$t=$cte}}=\frac{-nRt}{p^2}. \]

Del mismo modo, la tasa de variación instantánea del volumen con respecto a la temperatura es:

\[ \frac{\partial v}{\partial t}(t,p)=\frac{d}{dt}\left(\frac{nRt}{p}\right)_{\mbox{$p=$cte}}=\frac{nR}{p}. \]

12.5 Vector gradiente

Definición 12.9 (Vector gradiente) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, se llama gradiente de $f$, y se escribe $\nabla f$, a la función que a cada punto $a=(a_1,\ldots,a_n)$ le asigna el vector cuyas componentes son las derivadas parciales de $f$ en $a$,

\[\nabla f(a)=\left(\frac{\partial f}{\partial x_1}(a),\ldots,\frac{\partial f}{\partial x_n}(a)\right).\]

Más adelante se mostrará que vector gradiente en un punto dado tiene la misma magnitud y dirección que la velocidad máxima de variación de la función en ese punto. De este modo, $\nabla f(a)$ indica la dirección de máximo crecimiento de la función, mientras que $-\nabla f(a)$ indica la dirección de máximo decrecimiento.

Ejemplo 12.10 Al calentar una superficie la temperatura $t$ (en ºC) en cada punto $(x,y,z)$ (en m) de dicha superficie viene dada por la función:

\[ t(x,y,z)=\frac{x}{y}+z^2. \]

La dirección en la que más rápidamente aumenta la temperatura nos la da el vector gradiente

\[ \nabla t(x,y,z)=\left(\frac{\partial t}{\partial x}(x,y,z),\frac{\partial t}{\partial y}(x,y,z),\frac{\partial t}{\partial z}(x,y,z)\right)=\left(\frac{1}{y},\frac{-x}{y^2},2z\right). \]

Si estamos, por ejemplo, en el punto $(2,1,1)$ dicha dirección será

\[ \nabla t(2,1,1)=\left(\frac{1}{1},\frac{-2}{1^2},2\cdot 1\right)=(1,-2,2), \]

y su magnitud

\[ |\nabla f(2,1,1)|=|\sqrt{1^2+(-2)^2+2^2}|=|\sqrt{9}|=3 \mbox{ $^\circ$C/m}. \]

12.6 Recta normal y plano tangente a una superficie

Ya se ha visto que para una función de dos variables $f(x,y)$, $f'_{x}(a,b)$ es la pendiente de la recta tangente a la superficie de $f$ en $(a,b)$ en su intersección con el plano $y=b$, y que $f'_y(a,b)$ es la pendiente de la recta tangente a la superficie de $f$ en $(a,b)$ en su intersección con el plano $x=a$. Estas dos rectas tangentes definen, en realidad, un plano tangente a la superficie de $f$ en el punto $(a,b)$.

Si tomamos los vectores $(1, 0, f'_x(a,b))$ y $(0, 1, f'_y(a,b))$ en las direcciones de estas dos rectas tangentes, su producto vectorial será normal a la superficie.

\[\begin{align*} (0, 1, f'_y(a,b)) \times (1, 0, f'_x(a,b)) &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 1 & f'_y(a,b) \\ 1 & 0 & f'_x(a,b) \end{vmatrix} \\ &= f'_x(a,b) \mathbf{i} + f'_y(a,b) \mathbf{j} - \mathbf{z} \\ &= (f_x(a,b), f_y(a,b), -1) \end{align*}\]

Usando este vector podemos construir la ecuación de la recta normal a la superficie de $f$.

Definición 12.10 (Recta normal a la superficie de una función de dos variables) Dada una función de dos variables $f(x,y)$ con derivadas parciales continuas en el punto $(a,b)$ se define la recta normal a la superficie de $f$ en el punto $(a,b)$ como la recta de ecuación

\[ \begin{gathered} (a, b, f(a,b)) + t \left(\frac{\partial f}{\partial x}(a,b), \frac{\partial f}{\partial y}(a,b), -1\right) \\ = \left(a+t\frac{\partial f}{\partial x}(a,b), b+t\frac{\partial f}{\partial y}(a,b), f(a,b)-t\right). \end{gathered} \]

Para obtener la ecuación del plano tangente a la superficie de $f$ también podemos usar este vector normal a la superficie, ya que cualquier punto del plano debe cumplir la ecuación

\[ \begin{gathered} ((x,y,z)-(a,b,f(a,b)))\left(\frac{\partial f}{\partial x}(a,b), \frac{\partial f}{\partial y}(a,b), -1\right) = 0 \\ \Leftrightarrow (x-a)\frac{\partial f}{\partial x}(a,b) + (y-b)\frac{\partial f}{\partial y}(a,b) - (z-f(a,b)) = 0. \end{gathered} \]

Definición 12.11 (Plano tangente a la superficie de una función de dos variables) Dada una función de dos variables $f(x,y)$ con derivadas parciales continuas en el punto $(a,b)$ se define el plano tangente a la superficie de $f$ en el punto $(a,b)$ como el plano de ecuación

\[ z = \frac{\partial f}{\partial x}(a,b)(x-a) + \frac{\partial f}{\partial y}(a,b)(y-b)+f(a,b) \]

Ejemplo 12.11 La recta normal a la superficie de la función $f(x,y)=x^2+y^2$ en el punto $(1,1,2)$ tiene ecuación

\[ \begin{gathered} (1,1,2)+ t \left(\frac{\partial f}{\partial x}(1,1), \frac{\partial f}{\partial y}(1,1), -1\right) \\ = (1,1,2)+ t (2,2,-1) = (1+2t,1+2t,2-t). \end{gathered} \]

Y el plano tangente a la superficie de $f$ en $(1,1,2)$ tiene ecuación

\[\begin{align*} z &= \frac{\partial f}{\partial x}(1,1)(x-1) + \frac{\partial f}{\partial y}(1,1)(y-1)+f(1,1) \\ &= 2(x-1) + 2(y-1) + 2 = 2x+2y-2. \end{align*}\]

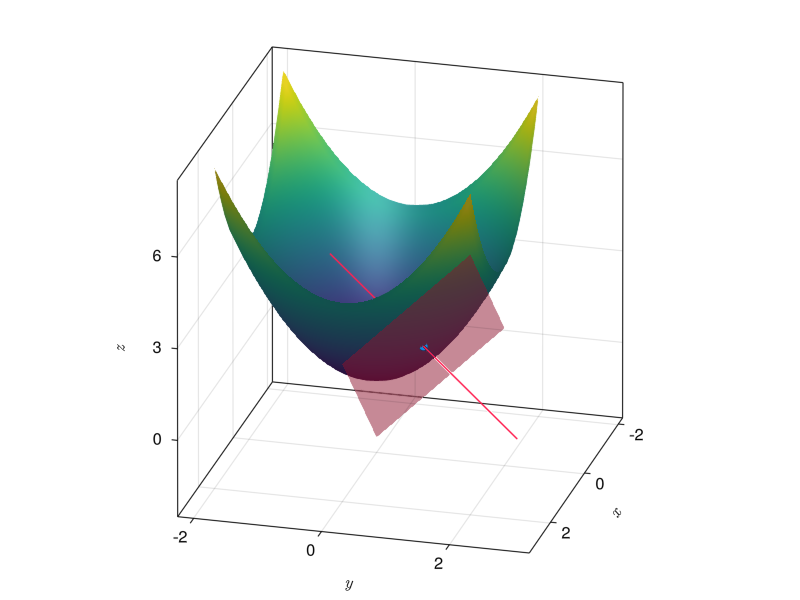
Recta normal y plano tangente a la función $f(x,y)=x^2+y^2$ en el punto $(1,1,2)$.

Advertencia

La existencia de las derivadas parciales de una función de dos variables $f(x,y)$ en un punto $(a,b)$ no garantiza la existencia de la recta normal y el plano tangente en ese punto.

Ejemplo 12.12 La función

\[ f(x,y) = \begin{cases} \frac{xy^2}{x^2+y^4} & \mbox{si $(x,y)\neq (0,0)$}\\ 0 & \mbox{si $(x,y) = (0,0)$} \end{cases} \]

Cuando $y=0$ esta función es constante y vale $0$ por lo que su derivada parcial con respecto a $x$ es $\frac{\partial f}{\partial x} = 0$. Del mismo modo, cuando $x=0$ esta función es constante y vale $0$ por lo que su derivada parcial con respecto a $y$ también se anula $\frac{\partial f}{\partial x} = 0$. Sin embargo, esta función no tiene plano tangente en el punto $(0,0)$ como se puede apreciar en la Figura 12.1.

12.7 Diferenciabilidad

En el capítulo de derivadas de funciones de una variable se definió el diferencial de una función $y=f(x)$ como la aplicación lineal $dy = f'(x)dx$ y se vió cómo el diferencial puede utilizarse para aproximar la variación de $f$ en un entorno de $x$. La misma idea puede generalizarse a funciones de varias variables.

Definición 12.12 (Diferencial total) Dada una función de $n$ variables $y=f(x_1,\ldots,x_n)$, se define el diferencial total de la función $f$ en el punto $P=(a_1, \ldots, a_n)$ como

\[ dy = \nabla f(P)(dx_1, \ldots, dx_n) = \frac{\partial f}{\partial x_1}(P)dx_1 + \cdots + \frac{\partial f}{\partial x_n}(P)dx_n \]

Ejemplo 12.13 Dada la función $u=f(x,y,z) = x^2+yz$, su gradiente es $\nabla f(x,y,z) = (2x, z, y)$, y en el punto $(1, 1, 1)$ vale $(2, 1, 1)$, por lo que el diferencial total de $f$ en $(1, 1, 1)$ es

\[ du = \nabla f(1, 1, 1)(dx, dy, dz) = (2, 1, 1)(dx, dy, dz) = 2dx + dy + dz. \]

Definición 12.13 (Función diferenciable de dos variables) Dada una función de dos variables $z=f(x,y)$, se dice que $f$ es diferenciable en el punto $(a,b)$ si

\[ \Delta z = f(a+\Delta x, b+\Delta y) - f(a,b) = \nabla f(a, b) (\Delta x, \Delta y) + \varepsilon_1 \Delta x + \varepsilon_2 \Delta y \]

con $\varepsilon_1$ y $\varepsilon_2 \to 0$ cuanto $(x,y)\to (a,b)$.

Si una función de dos variables es diferenciable en un punto $(a,b)$, podemos usar el diferencial total $dz$ como una aproximación de la variación $\Delta z$ que experimenta la función en cualquier punto $(x,y)$ en un entorno de $(a,b)$, ya que $\varepsilon_1 \Delta x + \varepsilon_2 \Delta y \to 0$ cuando $(x,y)\to (a,b)$, es decir,

\[ \Delta z \approx dz = \nabla f(a, b) (\Delta x, \Delta y) \]

Si en la ecuación anterior reescribimos $\Delta x = x-a$ y $\Delta y = y-b$, se tiene que

\[\begin{align*} \Delta z &= f(a+\Delta x, b+\Delta y) - f(a,b) \\ &\approx \nabla f(a, b) (\Delta x, \Delta y) \\ &= \frac{\partial f}{\partial x}(a,b)(x-a) + \frac{\partial f}{\partial y}(a,b)(y-b) \end{align*}\]

de donde se deduce que

\[ f(x, y) \approx \frac{\partial f}{\partial x}(a,b)(x-a) + \frac{\partial f}{\partial y}(a,b)(y-b) + f(a,b). \]

Si se observa bien, el lado derecho de esta igualdad es la ecuación del plano tangente a la superficie de $f$ en el punto $(a,b)$. De esta manera, si una $f$ es diferenciable en $(a,b)$ podemos aproximar el valor de la función en cualquier punto $(x,y)$ de un entorno de $(a,b)$, como el valor del plano tangente en ese punto. El error en la aproximación es $\varepsilon_1 \Delta x + \varepsilon_2 \Delta y$ que tiende a $0$ cuando $(x,y)$ se aproxima a $(a,b)$. Además, dado que $\varepsilon_1$ y $\varepsilon_2 \to 0$ cuando $(x,y)\to (a,b)$, la cantidad $\varepsilon_1 \Delta x + \varepsilon_2 \Delta y$ se aproxima a $0$ mucho más rápidamente que $\Delta x$ o $\Delta y$ se aproximan a $0$, por lo que el plano tangente a la superficie de $f$ en el punto $(a,b)$ dará muy buenas aproximaciones de $f$ en un entorno cercano de $(a,b)$.

Ejemplo 12.14 Veamos que la función $f(x,y)=x^2 + y^2$ es diferenciable en cualquier punto $(a,b)$

\[\begin{align*} \Delta z &= f(a+\Delta x, b+\Delta y) - f(a,b) = (a+\Delta x)^2 + (b+\Delta y)^2 - (a^2 + b^2) \\ &= a^2 + 2a\Delta x + \Delta x^2 + b^2 + 2b\Delta y + \Delta y^2 - a^2 - b^2\\ &= 2a\Delta x + 2b\Delta y + \Delta x^2 + \Delta y^2 \\ &= \frac{\partial f}{\partial x}(a,b) \Delta x + \frac{\partial f}{\partial y}(a,b) + \Delta x \Delta x + \Delta y \Delta y \end{align*}\]

De modo que, tomando $\varepsilon_1 = \Delta x$ y $\varepsilon_2 = \Delta y$, se tiene que

\[ \Delta z = \frac{\partial f}{\partial x}(a,b) \Delta x + \frac{\partial f}{\partial y}(a,b) + \varepsilon_1 \Delta x + \varepsilon_2 \Delta y \]

y, además $\varepsilon_1\to 0$ y $\varepsilon_2\to 0$ cuando $(x,y)\to (a,b)$, por lo que la función $f$ es diferenciable en $(a,b)$.

Así pues, podemos utilizar el plano tangente $z = 2x+2y-2$ que calculamos en el Ejemplo 12.11 para aproximar la función en un entorno del punto $(1, 1, 2)$. Por ejemplo, la aproximación de $f$ en $(0.9, 1.2)$ es

\[ f(0.9, 1.2) \approx 2\cdot 0.9 + 2\cdot 1.2 - 2 = 2.2. \]

El concepto de función diferenciable se generaliza de manera natural para funciones de $n$ variables.

Definición 12.14 (Función diferenciable) Dada una función de n variables $z=f(x_1,\ldots,x_n)$, se dice que $f$ es diferenciable en el punto $(a_1,\ldots,a_n)$ si

\[\begin{align*} \Delta z &= f(a_1+\Delta x_1, \ldots, a_n+\Delta x_n) - f(a_1,\ldots,a_n) \\ &= \nabla f(a_1,\ldots,a_n) (\Delta x_1,\ldots, \Delta x_n) + (\varepsilon_1,\ldots, \varepsilon_n)(\Delta x_1,\ldots, \Delta x_n) \end{align*}\]

con $(\varepsilon_1,\ldots, \varepsilon_n) \to (0,\ldots,0)$ cuando $(x_1,\ldots,x_n)\to (a_1,\ldots,a_n)$.

En general, demostrar que una función es diferenciable en un punto puede ser una tarea complicada, pero afortunadamente, el siguiente teorema proporciona una condición suficiente para que una función sea diferenciable.

Teorema 12.1 Si una función de $n$ variables $f(x_1,\ldots,x_n)$ tiene derivadas parciales continuas en un entorno de $(a_1,\ldots,a_n)$, entonces $f$ es diferenciable en $(a_1,\ldots,a_n)$.

Demostración

Prueba. Veremos la demostración en el caso de una función de dos variables $f(x,y)$.

\[\begin{align*} \Delta z &= f(a+\Delta x, b+\Delta y) - f(a,b) \\ &= f(a+\Delta x, b+\Delta y) - f(a+\Delta x, b) + f(a+\Delta x, b) - f(a,b) \end{align*}\]

Como en los dos primeros términos de esta expresión se mantiene constante $a+\Delta x$, podemos considerar la función parcial $f_2(y)$ que resulta de fijar el valor de $x$ a $a+\Delta x$, de manera que $f(a+\Delta x, b+\Delta y) - f(a+\Delta x, b) = f_2(b+\Delta y)-f_2(b)$. Entonces, como $f'_2(y)=\frac{\partial f}{\partial y}(a+\Delta x, y)$ existe en el intervalo $[b, b+\Delta y]$, por el teorema del valor medio (Teorema 7.6), existe un valor $b_0\in(b, b+\Delta y)$ tal que

\[ f(a+\Delta x, b+\Delta y) - f(a+\Delta x, b) = \frac{\partial f}{\partial y}(a+\Delta x, b_0) \Delta y. \]

Del mismo modo, como en $f(a+\Delta x, b) - f(a,b)$ se mantiene constante $b$, podemos considerar la función parcial $f_1(x)$ que resulta de fijar $y=b$, de manera que $f(a+\Delta x, b) - f(a,b)=f_1(a+\Delta x)-f_1(a)$. Al igual que antes, como $f'_1(y)=\frac{\partial f}{\partial x}(x, b)$ existe en el intervalo $[a, a+\Delta x]$, por el teorema del valor medio, existe otro valor $a_0\in(a, a+\Delta x)$ tal que

\[ f(a+\Delta x, b) - f(a,b) = \frac{\partial f}{\partial x}(a_0, b) \Delta x. \]

Por tanto, la expresión inicial se puede reescribir como

\[\begin{align*} \Delta z &= f(a+\Delta x, b+\Delta y) - f(a,b) \\ &= \frac{\partial f}{\partial x}(a_0, b) \Delta x + \frac{\partial f}{\partial y}(a+\Delta x, b_0) \Delta y. \end{align*}\]

Si ahora definimos

\[\begin{align*} \varepsilon_1 &= \frac{\partial f}{\partial x}(a_0,b)-\frac{\partial f}{\partial x}(a,b),\\ \varepsilon_2 &= \frac{\partial f}{\partial y}(a+\Delta x, b_0)-\frac{\partial f}{\partial y}(a,b), \end{align*}\]

se tiene que

\[\begin{align*} \Delta z &= \left(\varepsilon_1 + \frac{\partial f}{\partial x}(a, b)\right)\Delta x + \left(\varepsilon_2 + \frac{\partial f}{\partial y}(a, b)\right)\Delta y \\ &= \frac{\partial f}{\partial x}(a, b)\Delta x + \frac{\partial f}{\partial y}(a, b)\Delta y + \varepsilon_1\Delta x + \varepsilon_2\Delta y. \end{align*}\]

Finalmente, como las derivadas parciales de $f$ son continuas en un entorno de $(a,b)$, cuando $\Delta x\to 0$ y $\Delta y\to 0$, se tiene que $\frac{\partial f}{\partial x}(a_0,b)\to \frac{\partial f}{\partial x}(a,b)$, y $\frac{\partial f}{\partial y}(a+\Delta x, b_0)\to \frac{\partial f}{\partial y}(a,b)$, de manera que, $\varepsilon_1\to 0$ y $\varepsilon_2\to 0$, por lo que se concluye que $f$ es diferenciable en $(a,b)$.

Esta demostración puede generalizarse fácilmente a funciones de $n$ variables.

12.8 Regla de la cadena

En el Teorema 7.2 vimos cómo calcular la derivada de una composición de dos funciones de una variable real. Una función de varias variables también puede componerse con otras funciones, y en particular, resulta interesante estudiar la derivada de la composición de una función vectorial con una función de varias variables.

Si $f:\mathbb{R}^n\rightarrow \mathbb{R}$ es una función de $n$ variables y $g:\mathbb{R}\rightarrow \mathbb{R}^n$ es una función vectorial en $\mathbb{R}^n$, entonces es posible componer $g$ con $f$, de manera que $f\circ g:\mathbb{R}\rightarrow \mathbb{R}$ es una función real de variable real.

Teorema 12.2 (Regla de la cadena) Si $z=f(x_1,\ldots,x_n)$ es una función de $n$ variables diferenciable y $g(t)=(x_1(t),\ldots,x_n(t))$ es una función vectorial en $\mathbb{R}^n$ diferenciable, entonces

\[ \frac{dz}{dt} = (f\circ g)'(t) = \nabla f(g(t))\cdot g'(t) = \frac{\partial z}{\partial x_1}\frac{dx_1}{dt} + \cdots +\frac{\partial z}{\partial x_n}\frac{dx_n}{dt} \]

Demostración

Prueba. Como $f$ es diferenciable se tiene que

\[ \Delta z = \nabla f(a_1,\ldots,a_n) (\Delta x_1,\ldots, \Delta x_n) + (\varepsilon_1,\ldots, \varepsilon_n)(\Delta x_1,\ldots, \Delta x_n) \]

con $(\varepsilon_1,\ldots,\varepsilon_n) \to (0,\ldots,0)$ cuando $(\Delta x_1, \ldots, \Delta x_n) \to (0,\ldots,0)$.

Entonces, tomando $\Delta t\neq 0$ se tiene

\[\begin{align*} \frac{\Delta z}{\Delta t} &= \nabla f(a_1,\ldots,a_n) \frac{(\Delta x_1,\ldots, \Delta x_n)}{\Delta t} + (\varepsilon_1,\ldots, \varepsilon_n) \frac{(\Delta x_1,\ldots, \Delta x_n)}{\Delta t} \\ &= \nabla f(a_1,\ldots,a_n) \left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) + (\varepsilon_1,\ldots, \varepsilon_n) \left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) \end{align*}\]

Y tomando el límite cuando $\Delta t \to 0$ se concluye

\[\begin{align*} \frac{dz}{dt} &= \lim_{\Delta t\to 0}\frac{\Delta z}{\Delta t} \\ &= \lim_{\Delta t\to 0} \nabla f(a_1,\ldots,a_n) \left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) + (\varepsilon_1,\ldots, \varepsilon_n) \left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) \\ &= \nabla f(a_1,\ldots,a_n) \lim_{\Delta t\to 0}\left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) + \lim_{\Delta t \to 0}(\varepsilon_1,\ldots, \varepsilon_n) \left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) \\ &= \nabla f(a_1,\ldots,a_n) \left(\frac{dx_1}{dt},\ldots, \frac{dx_n}{dt}\right) \end{align*}\]

ya que cuando $\Delta t \to 0$ $(\Delta x_1, \ldots, \Delta x_n) \to (0,\ldots,0)$, y por tanto, $(\varepsilon_1,\ldots,\varepsilon_n) \to (0,\ldots,0)$, por lo que

\[ \lim_{\Delta t\to 0} (\varepsilon_1,\ldots, \varepsilon_n) \left(\frac{\Delta x_1}{\Delta t},\ldots, \frac{\Delta x_n}{\Delta t}\right) = 0. \]

Ejemplo 12.15 Si se toma el campo escalar del plano real $f(x,y)=x^2y$ y la función vectorial $g(t)=(\cos(t),\operatorname{sen}(t))$ $t\in [0,2\pi]$ del mismo plano, entonces

\[ \nabla f(x,y) = (2xy, x^2), \]

\[ g'(t) = (-\operatorname{sen}(t), \cos(t)), \]

por lo que

\[\begin{align*} (f\circ g)'(t) &= \nabla f(g(t))\cdot g'(t) \\ &= (2\cos(t)\operatorname{sen}(t),\cos(t)^2)\cdot (-\operatorname{sen}(t),\cos(t)) \\ &= -2\cos(t)\operatorname{sen}(t)^2+\cos(t)^3. \end{align*}\]

Se puede llegar al mismo resultado, sin aplicar la regla de la cadena, derivando directamente la función compuesta

\[ (f\circ g)(t) = f(g(t)) = f(\cos(t), \operatorname{sen}(t)) = \cos(t)^2\operatorname{sen}(t), \]

de manera que

\[\begin{align*} (f\circ g)'(t) &= 2\cos(t)(-\operatorname{sen}(t))\operatorname{sen}(t)+\cos(t)^2 \cos(t)\\ &= -2\cos(t)\operatorname{sen}(t)^2+\cos(t)^3. \end{align*}\]

La regla de la cadena para la composición de una función vectorial con una función de varias variables permite obtener fácilmente el álgebra de derivadas para funciones reales de una variable real:

\[ \begin{aligned} (u+v)' &= u'+v'\\ (uv)' &= u'v+uv'\\ \left(\frac{u}{v}\right)' &= \frac{u'v-uv'}{v^2}\\ (u\circ v)' &= u'(v)v' \end{aligned} \]

Por ejemplo, para deducir la derivada de la suma se toma la función de dos variables $f(x,y)=x+y$ y la función vectorial $g(t)=(u(t),v(t))$, de manera que aplicando la regla de la cadena se tiene

\[\begin{align*} (u+v)'(t) &= (f\circ g)'(t) = \nabla f(g(t))\cdot g'(t) \\ &= (1,1)\cdot (u'(t),v'(t)) = u'(t)+v'(t). \end{align*}\]

Y para deducir derivada del producto, tomando $f(x,y)=xy$, se tiene

\[\begin{align*} (uv)'(t) &= (f\circ g)'(t) = \nabla f(g(t))\cdot g'(t) \\ &= (v(t),u(t))\cdot (u'(t),v'(t)) = u'(t)v(t)+u(t)v'(t). \end{align*}\]

12.9 Derivación implícita

Hasta ahora hemos estado trabajando con funciones de varias variables explícitas, es decir, de la forma $y=f(x_1,\ldots,x_n)$, pero también es posible definir una función de varias variables de manera implícita mediante una ecuación de la forma $F(x_1,\ldots,x_n, y)=0$, donde $y=f(x_1,\ldots,x_n)$.

Ejemplo 12.16 La ecuación $x^2+y^2+z^2 = 1$ define la esfera de radio 1 centrada en el origen. Esta ecuación no define una función implícita $z=f(x,y)$ ya que si despejamos $z$ se tiene que $z=\pm\sqrt{1-x^2-y^2}$, que no es una función ya que asigna dos imágenes a cada punto $(x,y)$. Sin embargo, si se toma sólo la raíz positiva, la ecuación anterior define de manera implícita la función $z=\sqrt{1-x^2-y^2}$ que corresponde a la semiesfera positiva de radio 1 centrada en el origen.

El teorema siguiente nos proporciona las condiciones suficientes para que una ecuación como la anterior defina de manera implícita a una de sus variables como función de las otras.

Teorema 12.3 (Teorema de la función implícita) Si $F(x_1,\ldots,x_n,y)$ es una función de $n+1$ variables definida sobre un entorno abierto del punto $(a_1,\ldots,a_n,b)$ y tal que

$F(a_1,\ldots,a_n,b)=0$
Todas las derivadas parciales de $F$ son continuas en el entorno de $(a_1,\ldots,a_n,b)$.
$\frac{\partial F}{\partial y}\neq 0$.

Entonces la ecuación $F(x_1,\ldots,x_n,y)=0$ define a $y$ como una función de $x_1, .\ldots, x_n$ en el entorno de $(a_1,\ldots,a_n,b)$.

Cuando una ecuación define de manera implícita una de sus variables como función de las otras, no siempre es posible obtener la forma explícita de esa función, por lo que necesitamos saber cómo calcular la derivada de estas funciones en forma implícita.

Teorema 12.4 Si $F(x_1,\ldots,x_n,y)=0$ define a $y$ implícitamente como función derivable de $x_1,\ldots,x_n$, entonces

\[ \frac{\partial y}{\partial x_i} = -\frac{F'_{x_i}(x_1,\ldots,x_n,y)}{F'_{y}(x_1,\ldots,x_n,y)}. \]

Demostración

Prueba. Si la ecuación $F(x_1,\ldots,x_n,y)=0$ define a $y$ como una función de $x_1, \ldots, x_n$, es decir, $y=f(x_1,\ldots,x_n)$, entonces, tomando $z=F(x_1,\ldots,x_n,f(x_1,\ldots,x_n))$ y aplicando la regla de la cadena se tiene

\[\begin{align*} \frac{\partial z}{\partial x_i} &= F'_{x_1}(x_1,\ldots,x_n,y)\frac{\partial x_1}{\partial x_i} + \cdots + F'_{x_n}(x_1,\ldots,x_n,y)\frac{\partial x_n}{\partial x_i} + F'_{y}(x_1,\ldots,x_n,y)\frac{\partial y}{\partial x_i} \\ &= F'_{x_i}(x_1,\ldots,x_n,y) + F'_{y}(x_1,\ldots,x_n,y)\frac{\partial y}{\partial x_i} = 0 \end{align*}\] de donde se deduce

\[ \frac{\partial y}{\partial x_i} = -\frac{F'_{x_i}(x_1,\ldots,x_n,y)}{F'_{y}(x_1,\ldots,x_n,y)}. \]

Ejemplo 12.17 La ecuación $x^2+y^2=1$ define a la circunferencia de radio 1 centrada en el origen de coordenadas, que también puede expresarse como

\[ F(x,y) = x^2+y^2-1 = 0. \]

Si se piensa en $y$ como función implícita de $x$, es decir, $y=f(x)$, se tiene

\[ y'=-\frac{F'_x(x,y)}{F'_y(x,y)} = -\frac{2x}{2y}=-\frac{x}{y}. \]

Podría llegarse al mismo resultado, despejando $y$ de la ecuación de la circunferencia,

\[ x^2+y^2=1 \Leftrightarrow y^2=1-x^2 \Leftrightarrow y= \pm\sqrt{1-x^2}. \]

Si se toma la raíz positiva, que corresponde a la semicircunferencia superior, la derivada vale

\[ y' = \frac{1}{2\sqrt{1-x^2}}(-2x) = \frac{-x}{\sqrt{1-x^2}}, \]

que coincide con el resultado de la derivación implícita, teniendo en cuenta que $y=\sqrt{1-x^2}$.

12.10 Derivada direccional

Hemos visto que para una función de dos variables $f(x,y)$, $f'_x(a,b)$ es la tasa de variación instantánea de $f$ con respecto a $x$ en el punto $(a,b)$, es decir, cuando nos desplazamos desde el punto $(a,b)$ en la dirección del eje $X$, y que $f'_y(a,b)$ es la tasa de variación instantánea de $f$ con respecto a $y$ en el punto $(a,b)$, es decir, cuando nos desplazamos desde el punto $(a,b)$ en la dirección del eje $Y$.

Pero, ¿qué pasa si nos movemos en cualquier otra dirección?

La tasa de variación instantánea de $f$ en un punto $(a,b)$ en la dirección de un vector unitario cualquiera $u$ se conoce como derivada direccional.

Definición 12.15 (Derivada direccional) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, un punto $P$ y un vector unitario $\mathbf{u}$ en $\mathbb{R}^n$, el límite

\[ f'_{\mathbf{u}}(P) = \lim_{h\rightarrow 0}\frac{f(P+h\mathbf{u})-f(P)}{h}, \]

cuando existe, se llama derivada direccional de $f$ en el punto $P$ en la dirección de $\mathbf{u}$.

Obsérvese que las derivadas parciales son las derivadas direccionales en las direcciones de los vectores coordenados.

El siguiente teorema nos permitirá calcular derivadas direccionales de manera más sencilla, sin necesidad de calcular el límite anterior.

Teorema 12.5 Si $f:\mathbb{R}^n\rightarrow \mathbb{R}$ es una función de $n$ variables cuyas derivadas parciales existen en un punto $P$ y $\mathbf{u}$ es un vector unitario en $\mathbb{R}^n$, entonces

\[ f'_{\mathbf{u}}(P) = \nabla f(P)\cdot \mathbf{u}. \]

Demostración

Prueba. Si se considera un vector unitario $\mathbf{u}$, la función vectorial cuya trayectoria pasa por $P$, dirigida por $\mathbf{u}$, tiene ecuación

\[ g(t)=P+t\mathbf{u},\ t\in\mathbb{R}, \]

que para $t=0$, pasa por $P=g(0)$ con velocidad $\mathbf{u}=g'(0)$.

Así, la tasa de variación de $f$ en el punto $P$ en la dirección de $\mathbf{u}$ es

\[ (f\circ g)'(0) = \nabla f(g(0))\cdot g'(0) = \nabla f(P)\cdot \mathbf{u}. \]

En el caso de una función de dos variables $f(x,y)$, la derivada direccional $f_{\mathbf{u}}(a,b)$ da la tasa de variación de $f$ en el punto $(a,b)$ cuando empezamos a cambiar $x$ e $y$ en la dirección del vector $\mathbf{u}$.

Ejemplo interactivo con Geogebra

Ejemplo 12.18 Dada la función $f(x,y) = x^2+y^2$, su vector gradiente es

\[ \nabla f(x,y) = (2x,2y), \]

de manera que la derivada direccional en el punto $(1,1)$, en la dirección del vector unitario $\mathbf{u}=(1/\sqrt{2},1/\sqrt{2})$ es

\[ f'_{\mathbf{u}}(1,1) = \nabla f(1,1)\cdot \mathbf{u} = (2,2)\cdot(1/\sqrt{2},1/\sqrt{2}) = \frac{2}{\sqrt{2}}+\frac{2}{\sqrt{2}} = \frac{4}{\sqrt{2}}. \]

Para calcular la derivada direccional en la dirección de un vector no unitario $\mathbf{v}$, basta con convertirlo en unitario mediante la transformación

\[ \mathbf{v'}=\frac{\mathbf{v}}{|\mathbf{v}|}. \]

Teorema 12.6 Si $f:\mathbb{R}^n\rightarrow \mathbb{R}$ es una función de $n$ variables cuyas derivadas parciales existen en un punto $P$ entonces la dirección de máximo crecimiento de $f$ es la del vector gradiente $\nabla f(P)$.

Demostración

Prueba. Como se ha visto, para un vector unitario $\mathbf{u}$

\[ f'_{\mathbf{u}}(P) = \nabla f(P)\cdot \mathbf{u} = |\nabla f(P)|\cos(\theta), \]

donde $\theta$ es el ángulo que forma $\mathbf{u}$ con el vector gradiente $\nabla f(P)$.

Teniendo en cuenta que $-1\leq \cos(\theta)\leq 1$, para cualquier vector $\mathbf{u}$ se cumple

\[ -|\nabla f(P)|\leq f'_{\mathbf{u}}(P)\leq |\nabla f(P)|. \]

Además, si $\mathbf{u}$ tiene la misma dirección y sentido que el gradiente, se tiene

\[ f'_{\mathbf{u}}(P)=|\nabla f(P)| \cos(0)= |\nabla f(P)|. \]

Por tanto, el crecimiento máximo de un campo escalar se produce en la dirección y sentido del gradiente.

Del mismo modo, si $\mathbf{u}$ tiene la misma dirección y sentido opuesto al gradiente, se tiene

\[ f'_{\mathbf{u}}(P)=|\nabla f(P)| \cos(\pi)=-|\nabla f(P)|. \]

Por tanto, el decrecimiento máximo de un campo escalar se produce en la dirección y sentido opuesto al gradiente.

Teorema 12.7 Sea $C$ el conjunto de nivel de una función de varias variables $f$ que incluye a un punto $P$. Si $\mathbf{v}$ es un vector tangente a una trayectoria que circule por $C$ en $P$, entonces

\[ \nabla f(P) \cdot \mathbf{v} = 0. \]

Es decir, el vector gradiente de $f$ en $P$ es normal a $C$ en $P$, siempre que no sea nulo.

Demostración

Prueba. Si se considera una trayectoria $g(t)$ a lo largo del conjunto de nivel $C$ que pase por $P=g(t_0)$, de modo que $\mathbf{v}=g'(t_0)$, entonces

\[ (f\circ g)(t) = f(g(t)) = C, \]

que es constante para cualquier $t$, y al aplicar la regla de la cadena se tiene

\[ (f\circ g)'(t) = \nabla f(g(t))\cdot g'(t) = 0, \]

de modo que, cuanto $t=t_0$, se tiene

\[ \nabla f(P)\cdot \mathbf{v} = 0. \]

Según el resultado anterior, la recta normal a una línea $f(x,y)=0$ en un punto $P=(a,b)$, tiene ecuación

\[ P+t\nabla f(P) = (a, b) + t \nabla f(a,b). \]

Ejemplo 12.19 Dado el campo escalar $f(x,y)=x^2+y^2-1$, y el punto $P=(0,1)$, resulta que el conjunto de nivel que pasa por $P$, para el que $f(x,y)=f(P)=0$ es la circunferencia de radio 1 centrada en el origen. Así pues, tomando como vector normal el gradiente de $f$, $\nabla f(x,y) = (2x,2y)$, que en el punto $P=(0,1)$ vale $\nabla f(0,1) = (0,2)$, la recta normal a la circunferencia en $P$ es

\[ P + t \nabla f(P) = (0,1) + t (0,2) = (0, 1+2t), \]

que se trata de la recta vertical $x=0$, que coincide con el eje $Y$.

Y la recta tangente a la circunferencia en $P$ es

\[\begin{align*} ((x,y)-P)\cdot \nabla f(P) &= ((x,y)-(0,1))\cdot (0,2) \\ &= (x, y-1)\cdot(0, 2) = 2(y-1) = 0 \\ &\Rightarrow y=1. \end{align*}\]

12.11 Derivadas de segundo orden

Las derivadas parciales de una función son, a su vez, funciones de varias variables que muchas veces pueden volverse a derivar parcialmente con respecto a alguna de sus variables.

Definición 12.16 (Derivadas parciales de segundo orden) Si una función $f(x_1,\ldots,x_n)$ tiene derivada parcial \[f'_{x_i}(x_1,\ldots,x_n)\] con respecto a la variable $x_i$ en un conjunto $A$, entonces podemos derivar de nuevo parcialmente $f'_{x_i}$ con respecto a la variable $x_j$. Esta segunda derivada, cuando existe, se llama derivada parcial de segundo orden de $f$ con respecto a las variables $x_i$ y $x_j$, y se nota

\[\frac{\partial ^2 f}{\partial x_j \partial x_i}= \frac{\partial}{\partial x_j}\left(\frac{\partial f}{\partial x_i}\right).\]

De forma análoga se definen las derivadas de orden superior.

Ejemplo 12.20 La función de dos variables \[f(x,y)=x^y\] tiene cuatro derivadas parciales de segundo orden, que son:

\[\begin{aligned} \frac{\partial^2 f}{\partial x^2}(x,y) &= \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}(x,y)\right) = \frac{\partial}{\partial x}\left(yx^{y-1}\right) = y(y-1)x^{y-2},\\ \frac{\partial^2 f}{\partial y \partial x}(x,y) &= \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}(x,y)\right) = \frac{\partial}{\partial y}\left(yx^{y-1}\right) = x^{y-1}+yx^{y-1}\log x,\\ \frac{\partial^2 f}{\partial x \partial y}(x,y) &= \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}(x,y)\right) = \frac{\partial}{\partial x}\left(x^y\log x \right) = yx^{y-1}\log x+x^y\frac{1}{x},\\ \frac{\partial^2 f}{\partial y^2}(x,y) &= \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}(x,y)\right) = \frac{\partial}{\partial y}\left(x^y\log x \right) = x^y(\log x)^2.\end{aligned}\]

En el ejemplo anterior se aprecia que las derivadas cruzadas de segundo orden $\frac{\partial^2 f}{\partial y\partial x}$ y $\frac{\partial^2 f}{\partial x\partial y}$ coinciden. El siguiente teorema establece bajo qué condiciones el orden de derivación no importa.

Teorema 12.8 (Igualdad de las derivadas cruzadas) Si $f(x_1,\ldots,x_n)$ es una función de $n$ variables tal que sus derivadas parciales $\frac{\partial^2 f}{\partial x_i\partial x_j}$ y $\frac{\partial^2 f}{\partial x_j\partial x_i}$ existen y son continuas en un conjunto abierto $A$, entonces para cualquier $(x,y)\in A$

\[ \frac{\partial^2 f}{\partial x_i\partial x_j}(x,y) = \frac{\partial^2 f}{\partial x_j\partial x_i}(x,y). \]

Demostración

Prueba. Por la definición de derivada parcial se tiene

\[\begin{align*} \frac{\partial^2 f}{\partial x \partial y} (a,b) &= \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)(a,b) = \lim_{\Delta x\to 0} \frac{f'_y(a+\Delta x,b)-f'_y(a,b)}{\Delta x} \\ &= \lim_{\Delta x\to 0} \frac{\lim_{\Delta y\to 0}\frac{f(a+\Delta x,b+\Delta y)-f(a+\Delta x,b)}{\Delta y} - \lim_{\Delta y\to 0}\frac{f(a,b+\Delta y)-f(a,b)}{\Delta y}}{\Delta x} \\ &= \lim_{\Delta x\to 0}\lim_{\Delta y\to 0} \frac{f(a+\Delta x, b+\Delta y)- f(a,b+\Delta y) -f(a+\Delta x, b) + f(a,b)}{\Delta x \Delta y} \end{align*}\]

Si se considera la función $g(t) = f(a+t, b+\Delta y)-f(a+t,b)$ en el intervalo $[0,\Delta x]$, como $f$ es derivable, $g$ es derivable, y por el teorema del valor medio, existe un valor $c\in (0,\Delta x)$ tal que

\[ \begin{gathered} \frac{f(a+\Delta x, b+\Delta y)- f(a,b+\Delta y) -f(a+\Delta x, b) + f(a,b)}{\Delta x} \\ = g'(c) = (f'_x(a+c, b+\Delta y) - f'_x(a+c,b)), \end{gathered} \]

de manera que, sustituyendo en la expresión anterior, se tiene

\[\begin{align*} \frac{\partial^2 f}{\partial x \partial y} (a,b) &= \lim_{\Delta x\to 0}\lim_{\Delta y\to 0} \frac{f'_x(a+c, b+\Delta y) - f'_x(a+c,b)}{\Delta y} \\ &= \lim_{\Delta x\to 0}\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)(a+c, b) \\ &= \lim_{\Delta x\to 0}\frac{\partial^2 f}{\partial y\partial x}(a+c, b). \end{align*}\]

Finalmente, como $\Delta x \to 0$, $c\to 0$, y como $\frac{\partial^2 f}{\partial y\partial x}$ es continua, se concluye que

\[ \frac{\partial^2 f}{\partial x \partial y} (a,b) = \frac{\partial^2 f}{\partial y \partial x} (a,b). \]

Una consecuencia del teorema es que, al calcular una derivada parcial de segundo orden que cumpla lo anterior, ¡el orden en que se realicen las derivadas parciales no importa!

12.12 Matriz hessiana

Definición 12.17 (Matriz hessiana) Dada una función de $n$ variables $f:\mathbb{R}^n\rightarrow \mathbb{R}$, para la que existen todas sus derivadas parciales de segundo orden en un punto $a=(a_1,\ldots,a_n)$, se define la matriz hessiana de $f$ en $a$, y se nota $\nabla^2f(a)$, como la matriz cuadrada cuyos elementos son

\[\nabla^2f(a)=\left( \begin{array}{cccc} \dfrac{\partial^2 f}{\partial x_1^2}(a) & \dfrac{\partial^2 f}{\partial x_1 \partial x_2}(a) & \cdots & \dfrac{\partial^2 f}{\partial x_1 \partial x_n}(a)\\ \dfrac{\partial^2 f}{\partial x_2 \partial x_1}(a) & \dfrac{\partial^2 f}{\partial x_2^2}(a) & \cdots & \dfrac{\partial^2 f}{\partial x_2 \partial x_n}(a)\\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{\partial^2 f}{\partial x_n \partial x_1}(a) & \dfrac{\partial^2 f}{\partial x_n \partial x_2}(a) & \cdots & \dfrac{\partial^2 f}{\partial x_n^2}(a) \end{array} \right).\]

Al determinante de esta matriz se le llama hessiano de $f$ en $a$, y se nota $Hf(a)=\lvert \nabla^2f(a)\rvert$.

Ejemplo 12.21 Consideremos de nuevo la función de dos variables $f(x,y)=x^y$. Su matriz hessiana es

\[\nabla^2f(x,y)=\left( \begin{array}{cc} \dfrac{\partial^2 f}{\partial x^2} & \dfrac{\partial^2 f}{\partial x \partial y}\\ \dfrac{\partial^2 f}{\partial y \partial x} & \dfrac{\partial^2 f}{\partial y^2} \end{array} \right) = \left( \begin{array}{cc} y(y-1)x^{y-2} & x^{y-1}(y\log x+1) \\ x^{y-1}(y\log x+1) & x^y(\log x)^2 \end{array} \right).\]

En el punto $(1,2)$ la matriz vale

\[\nabla^2f(1,2)=\left( \begin{array}{cc} 2(2-1)1^{2-2} & 1^{2-1}(2\log 1+1) \\ 1^{2-1}(2\log 1+1) & 1^2(\log 1)^2 \end{array} \right) = \left( \begin{array}{cc} 2 & 1 \\ 1 & 0 \end{array} \right).\]

Y el hessiano en dicho punto vale

\[Hf(1,2)=\left| \begin{array}{cc} 2 & 1 \\ 1 & 0 \end{array} \right|= 2\cdot 0-1\cdot1= -1. \]

Si el teorema de la igualdad de las derivadas cruzadas se cumple para todas las derivadas parciales de segundo orden, entonces la matriz hessiana es simétrica..

12.13 Extremos

Definición 12.18 (Máximo y mínimo relativos) Dada una función de $n$ variables $f:\mathbb{R}^n\to \mathbb{R}$, se dice que un punto $P$ es un máximo relativo de $f$ si existe un valor $\epsilon>0$ tal que

\[ f(P)\geq f(Q)\ \forall Q, |\vec{PQ}|<\epsilon. \]

Del mismo modo se dice que un punto $P$ es un mínimo relativo de $f$ si existe un valor $\epsilon>0$ tal que

\[ f(P)\leq f(Q)\ \forall Q, |\vec{PQ}|<\epsilon. \]

A los máximos y mínimos de $f$ se les conoce como extremos relativos de $f$.

Para determinar los extremos de una función de varias variables utilizaremos sus derivadas, de forma parecida a como lo hicimos para funciones de una variable.

Proposición 12.1 Si $f:\mathbb{R}^n\to \mathbb{R}$ es una función de $n$ variables, con derivadas parciales, que tiene un extremo relativo en el punto $P$, entonces

\[ \nabla f(P) = \mathbf{0}. \]

Demostración

Prueba. Tomando la trayectoria que pasa por $P$ con la dirección y sentido del gradiente,

\[ g(t)=P+t\nabla f(P), \]

la función $h=(f\circ g)(t)$ nunca decrece ya que

\[ h'(t) = (f\circ g)'(t) = \nabla f(g(t))\cdot g'(t) = \nabla f(P)\cdot \nabla f(P) = |\nabla f(P)|^2\geq 0. \]

y sólo se anula si $\nabla f(P)= \mathbf{0}$.

Así pues, si $\nabla f(P)\neq \mathbf{0}$, entonces $P$ no puede ser un máximo ya que siguiendo la trayectoria de $g$ desde $P$ se encontrarían puntos en los que la imagen de $f$ es mayor que en $P$. Del mismo modo, siguiendo la trayectoria opuesta a $g$ se encontrarían puntos en los que la imagen de $f$ es menor que la imagen en $P$, por lo que tampoco puede ser un mínimo.

A los puntos donde se anula el vector gradiente, se les denomina puntos críticos.

Ejemplo 12.22 Para el campo escalar $f(x,y)=x^2+y^2$, resulta evidente que sólo tiene un mínimo en el origen $(0,0)$ ya que

\[ f(0,0)=0 \leq f(x,y)=x^2+y^2,\ \forall x,y\in \mathbb{R}. \]

En este punto se cumple, $\nabla f(0,0) = (0,0)$.

12.13.1 Puntos de silla

No todos los puntos críticos son extremos. Si se considera, por ejemplo, el campo escalar $f(x,y)=y^2-x^2$, su gradiente es

\[\nabla f(x,y) = (2y,-2x),\]

que sólo se anula en el punto $(0,0)$. Sin embargo, este punto no es un mínimo relativo ya que los puntos $(x,0)$ del eje $X$ tienen imágenes $f(x,0) = -x^2 \leq 0 = f(0,0)$, y tampoco es un máximo relativo ya que los puntos $(0,y)$ del eje $Y$ tienen imágenes $f(0,y)= y^2 \geq 0 = f(0,0)$. Este tipo de puntos que anulan el gradiente pero que no son extremos, se conocen como puntos de silla.

Punto de silla de la función $f(x,y)=y^2-x^2$.

De la fórmula de Taylor de segundo grado para un campo escalar $f$ en un punto $P$ se deduce que

\[ f(P+\mathbf{v})-f(P)\approx \nabla f(P)\mathbf{v}+\frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}. \]

De manera que si $P$ es un punto crítico de $f$, como $\nabla f(P)=\mathbf{0}$, se tiene que

\[ f(P+\mathbf{v})-f(P)\approx \frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}. \]

Por tanto, el signo de $f(P+\mathbf{v})-f(P)$ coincide con el signo del término cuadrático $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}$.

Se pueden dar cuatro posibilidades:

Definido positivo: $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}>0$ $\forall \mathbf{v}\neq 0$.
Definido negativo: $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}<0$ $\forall \mathbf{v}\neq 0$.
Indefinido: $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}>0$ para algún $\mathbf{v}\neq 0$ y $\nabla^2f(P)\mathbf{u}\cdot\mathbf{u}<0$ para algún $\mathbf{u}\neq 0$.
Semidefinido: Cualquier otro caso distinto de los anteriores.

Así pues, dependiendo el signo de $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}$, se tiene

Teorema 12.9 Dado un punto crítico $P$ de una función de $n$ variables $f$ que tiene matriz hessiana $\nabla^2 f(P)$, se cumple

Si $\nabla^2f(P)$ es definido positivo entonces $f$ tiene un mínimo relativo en $P$.
Si $\nabla^2f(P)$ es definido negativo entonces $f$ tiene un máximo relativo en $P$.
Si $\nabla^2f(P)$ es indefinido entonces $f$ tiene un punto de silla en $P$.

En el caso de que $\nabla^2f(P)$ sea semidefinido, no se puede obtener ninguna conclusión y hay que recurrir a derivadas parciales de orden superior.

En el caso particular de una función de dos variables se tiene

Teorema 12.10 Dado un punto crítico $(a, b)$ de una función de dos variables $f(x,y)$ que tiene matriz hessiana $\nabla^2f(a,b)$, se cumple

Si $|\nabla^2 f(a,b)|>0$ y $\frac{\partial^2 f}{\partial x^2}(a,b)>0$ entonces $f$ tiene un mínimo relativo en $(a,b)$.
Si $|\nabla^2 f(a,b)|>0$ y $\frac{\partial^2 f}{\partial x^2}(a,b)<0$ entonces $f$ tiene un máximo relativo en $(a,b)$.
Si $|\nabla^2 f(P)|<0$ entonces $f$ tiene un punto de silla en $(a,b)$.

Demostración

Prueba. Tomando un vector unitario cualquiera $\mathbf{u}=(u_x,u_y)$, la derivada direccional de $f$ en $(a,b)$ es

\[ f'_u(a,b) = \nabla f(a,b)\mathbf{u} = f'_x(a,b)u_x + f'_y(a,b) u_y. \]

Y la derivada direccional de segundo orden es

\[\begin{align*} f''_{uu}(a,b) &= f'_u(f'_u)(a,b) = \nabla (f'_u)(a,b)\mathbf{u} = (f'_u)'_x(a,b)u_x + (f'_u)'_y(a,b) u_y \\ &= (f'_x u_x + f'_y u_y)'_x(a,b)u_x + (f'_x u_x + f'_y u_y.)'_y(a,b) u_y \\ &= f''_{xx}(a,b)u_x^2 + f''_{yx}(a,b)u_yu_x + f''_{xy}(a,b)u_xu_y + f''_{yy}(a,b)u_y^2 \\ &= f''_{xx}(a,b)u_x^2 + 2f''_{xy}(a,b)u_xu_y + f''_{yy}(a,b)u_y^2 \tag{1} \end{align*}\] (1) Aplicando el teorema de la igualdad de las derivadas cruzadas.

Completando el cuadrado de esta última expresión se tiene que

\[\begin{align*} f''_{uu}(a,b) &= f''_{xx}(a,b)\left(u_x+\frac{f''_{xy}(a,b)}{f''_{xx}(a,b)}u_y\right)^2+\frac{u_y^2}{f''_{xx}(a,b)}(f''_{xx}(a,b)f''_{yy}(a,b)-f''_{xy}(a,b)^2) \\ &= f''_{xx}(a,b)\left(u_x+\frac{f''_{xy}(a,b)}{f''_{xx}(a,b)}u_y\right)^2+\frac{u_y^2}{f''_{xx}(a,b)}|\nabla^2 f(a,b)| \end{align*}\]

Si $|\nabla ^2f(a,b)|>0$ y $f''_{xx}(a,b)>0$, como $\nabla ^2f(x,y)$ y $f''_{xx}(x,y)$ son continuas en un entorno de $(a,b)$, se tiene que $|\nabla ^2f(x,y)>0$ y $f''_{xx}(x,y)>0$ para $(x,y)$ en un entorno de $(a,b)$. Por tanto, observando la expresión anterior, podemos concluir que $f''_{uu}(x,y)>0$ en un entorno de $(a,b)$, es decir, la curva que interseca la superficie de $f$ con el plano que pasa por $(a,b,f(a,b))$ en la dirección de $\mathbf{u}$ es cóncava hacia arriba. Como esto esto es cierto para cualquier dirección $\mathbf{u}$, la gráfica de $f$ queda por encima del plano tangente en $(a,b,f(a,b))$ en un entorno de $(a,b)$, y por tanto, $f$ tienen un mínimo local en $(a,b)$.

Del mismo modo, $|\nabla ^2f(a,b)|>0$ y $f''_{xx}(a,b)<0$, podemos concluir que $f''_{uu}(x,y)<0$ en un entorno de $(a,b)$, es decir, la curva que interseca la superficie de $f$ con el plano que pasa por $(a,b,f(a,b))$ en la dirección de $\mathbf{u}$ es cóncava hacia abajo. Como esto esto es cierto para cualquier dirección $\mathbf{u}$, la gráfica de $f$ queda por debajo del plano tangente en $(a,b,f(a,b))$ en un entorno de $(a,b)$, y por tanto, $f$ tienen un máximo local en $(a,b)$.

Finalmente, si $|\nabla ^2f(a,b)<0$ los dos sumandos de la expresión de la derivada direccional de segundo orden anterior tienen signo distinto, y el signo de la derivada direccional dependerá de la dirección del vector $\mathbf{u}$, por lo que puede haber direcciones donde $f''_{uu}(x,y)>0$ y la curva que interseca la superficie de $f$ con el plano que pasa por $(a,b,f(a,b))$ en la dirección de $\mathbf{u}$ sea cóncava hacia arriba, y direcciones donde $f''_{uu}(x,y)<0$ y la curva que interseca la superficie de $f$ con el plano que pasa por $(a,b,f(a,b))$ en la dirección de $\mathbf{u}$ sea cóncava hacia abajo, de manera que $f$ tiene un punto de silla en $(a,b)$.

Ejemplo 12.23 Dado el campo escalar $f(x,y)=\dfrac{x^3}{3}-\dfrac{y^3}{3}-x+y$, se tiene que su gradiente vale

\[ \nabla f(x,y)= (x^2-1,-y^2+1), \]

que se anula en los puntos $(1,1)$, $(1,-1)$, $(-1,1)$ y $(-1,-1)$.

La matriz hessiana vale

\[ \nabla^2f(x,y) = \left( \begin{array}{cc} 2x & 0\\ 0 & -2y \end{array} \right) \]

y el hessiano vale

\[ |\nabla^2 f(x,y)| = -4xy. \]

Así pues, se tiene

Punto $(1,1)$: $|\nabla^2 f(1,1)| = -4 < 0 \Rightarrow$ Punto de silla.
Punto $(1,-1)$: $|\nabla^2 f(1,-1)|=4>0$ y $\frac{\partial^2}{\partial x^2}(1,-1)=2>0 \Rightarrow$ Mínimo relativo.
Punto $(-1,1)$: $|\nabla^2 f(-1,1)|=4>0$ y $\frac{\partial^2}{\partial x^2}(-1,1)=-2<0 \Rightarrow$ Máximo relativo.
Punto $(-1,-1)$: $|\nabla^2 f(-1,-1)|=-4<0 \Rightarrow$ Punto de silla.

12.14 Extremos condicionados

En ocasiones es interesante calcular los extremos relativos de una función de varias variables no en todo su dominio, sino en los puntos que cumple una o varias ecuaciones, como por ejemplo, calcular los extremos de la función $f(x,y)$ para los puntos que cumplen la ecuación $g(x,y)=0$. Cuando es posible despejar una de las variables de la ecuación y expresarla como una función explícita de la otra, se puede sustituir esa variable en $f$ y obtener una función de una variable, de manera que se pueden obtener sus extremos como se vio en el capítulo de derivadas de funciones de una variable.

Ejemplo 12.24 Si consideramos la misma función del ejemplo anterior $f(x,y)=\dfrac{x^3}{3}-\dfrac{y^3}{3}-x+y$, para calcular sus extremos relativos sujetos a la restricción $y+2x=0$, podemos sustituir $y=-2x$ en la fórmula de la función y se obtiene

\[ f(x,y) = f(x,-2x) = \frac{x^3}{3}-\frac{(-2x)^3}{3}-x-2x = 3x^3-3x \]

que es, en realidad, una función de una variable $f(x)=3x^3-3x$. Si calculamos su derivada y la igualamos a 0, se obtienen los puntos críticos $f'(x) = 9x^2-3 = 0 \Leftrightarrow x=\pm\sqrt{1/3}$. Como la segunda derivada es $f''(x) = 18x$, se tiene que $f''(-\sqrt{1/3})<0$ por lo que la función tiene un máximo local en $-\sqrt{1/3}$, y $f''(\sqrt{1/3})>0$ por lo que la función tiene un mínimo local en $\sqrt{1/3}$.

Ahora bien, cuando no es posible despejar una de las variables de la restricción $g(x,y)=0$, la cosa se complica. Afortunadamente, existe otro procedimiento para calcular los extremos de una función de varias variables sujeto a una o varias restricciones. A continuación explicamos el fundamento de este método para funciones de dos variables, aunque puede generalizarse para funciones de más de dos variables.

12.15 Multiplicadores de Lagrange

Dada una función de dos variables $f(x,y)$, si se quieren obtener los extremos de esta función sujetos a la restricción $g(x,y)=0$, en realidad, se trata de encontrar los extremos relativos de $f$ entre los puntos $(x,y)$ que están en la curva de nivel $g(x,y)=0$. Si dibujamos en el plano la curva de nivel de la ecuación junto a las curvas de nivel de $f$, el problema se reduce a encontrar el menor y el mayor valor de $k$ para el que la curva de nivel $f(x,y)=k$ se corta con la curva de nivel $g(x,y)=0$.

Ejemplo 12.25 La siguiente gráfica muestra las curvas de nivel de la función del ejemplo anterior $f(x,y)=\dfrac{x^3}{3}-\dfrac{y^3}{3}-x+y$ junto a la curva de nivel de la restricción $g(x,y)=y+2x=0$.

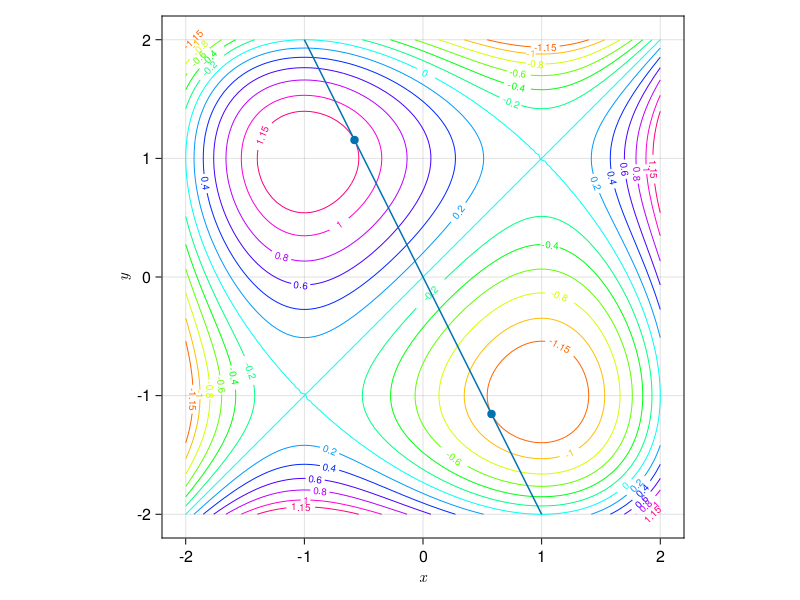
Como se aprecia en la gráfica el mayor valor de la curva de nivel de $f$ que se corta con la recta $y+2x=0$ es aproximadamente $1.15$ y ocurre en el punto $(-\sqrt{1/3}, 2\sqrt{1/3})$, y el menor valor de la curva de nivel de $f$ que se corta con la recta es aproximadamente $-1.5$ y ocurre en el punto $(\sqrt{1/3}, -2\sqrt{1/3})$.

En el ejemplo anterior se observa que los valores extremos se obtienen donde las curvas de nivel de la función y de la restricción son tangentes, y por tanto, sus vectores gradientes en los puntos de tangencia tendrán la misma dirección, es decir, si $(a,b)$ es un punto donde las curvas de nivel son tangentes, se tiene que

\[ \nabla f(a,b) = k \nabla g(a,b). \]

Al número $k$ de esta ecuación se le llama multiplicador de Lagrange, y este resultado da lugar al siguiente procedimiento para obtener los extremos de una función de varias variables con restricciones.

Teorema 12.11 (Multiplicadores de Lagrange) Dada una función de $n$ variables $f(x_1,\ldots,x_n)$, los extremos relativos de $f$ sujetos a la restricción $g(x_1,\ldots,x_n)=0$, si $\nabla g(x_1\ldots,x_n)\neq 0$, son los puntos que cumplen las ecuaciones

\[\begin{align*} \nabla F(x_1,\ldots,x_n) &= k\nabla g(x_1,\ldots,x_n) \\ g(x_1,\ldots, x_n) &= 0 \end{align*}\]

Demostración

Prueba. Daremos la prueba para 3 variables. Supongamos que $f(x,y,z)$ tiene un máximo relativo en el punto $(a,b,c)$ de la superficie definida por $g(x,y,z)=0$. Si consideramos una trayectoria con ecuación $\mathbf{f}(t)=(x(t),y(t),z(t))$ que esté sobre la superficie que define $g$ y tal que $\mathbf(f)(0)=(a,b,c)$, la función $h(t)=f(\mathbf{f}(t))$ tendrá un extremo relativo en $h(0)=f(\mathbf{f}(0))=f(a,b,c)$, y por tanto $h'(0)=0$. Pero, por otro lado, aplicando la regla de la cadena a la composición de $f$ y $\mathbf{f}$ se tiene

\[ h'(t) = f(\mathbf{f}(t))' = \nabla f(\mathbf{f}(t))\mathbf{f}'(t), \]

y en $t=0$ se cumple que

\[ h'(0) = f(\mathbf{f}(0))' = \nabla f(a,b,c)\mathbf{f}'(0) =0, \]

de donde se deduce que $\nabla f(a,b,c)$ es ortogonal a vector tangente a la trayectoria de $\mathbf{f}$ en $t=0$. Pero como la trayectoria de $\mathbf{f}$ está inscrita en la superficie de nivel de nivel $g(x,y,z)=0$, por el Teorema 12.7, si $\nabla g(a,b,c)\neq 0$ entonces también es ortogonal a $\mathbf{f}'(0)$, por lo que $\nabla f(a,b,c)$ y $\nabla g(a,b,c)$ deben ser paralelos, es decir,

\[ \nabla f(a,b,c) = k\nabla g(a,b,c) \]

Para dimensiones mayores la demostración es similar.

Ejemplo 12.26 Veamos cuáles son los extremos relativos de la función $f(x,y)=2x^2+y^2$ sobre los puntos de la circunferencia $x^2+y^2=1$.

Tomando $g(x,y)=x^2+y^2-1$, podemos expresar la circunferencia mediante la ecuación $g(x,y)=0$. Los extremos relativos de $f$ condicionados por $g(x,y)=0$, deben cumplir la ecuación de los multiplicadores de Lagrange

\[ \nabla f(x,y) = k \nabla g(x,y) \Leftrightarrow (4x, 2y) = k (2x, 2y), \]

de donde se deduce que deben cumplir las ecuaciones

\[ \begin{cases} 4x = 2kx\\ 2y = 2ky\\ x^2+y^2-1=0 \end{cases} \]

Resolviendo el sistema se obtienen cuatro soluciones en los puntos $(0,1)$, $(0,-1)$, $(1,0)$ y $(-1,0)$, y si evaluamos $f$ en cada uno de estos puntos se tiene

\[ f(0,1) = 1 \quad f(0,-1) = 1 \quad f(1,0)=2 \quad f(-1,0)=2, \]

por lo que se concluye que $f$ tiene máximos relativos en $(1,0)$ y $(-1,0)$, donde la función vale $2$, y mínimos relativos en $(0,1)$ y $(0,-1)$, donde la función vale $1$.

12.16 Polinomios de Taylor de funciones de varias variables

Ya se vio cómo aproximar funciones de una variable mediante polinomios de Taylor. Esto también se puede generalizar a la aproximación de funciones de varias variables mediante polinomios de varias variables.

12.16.1 Aproximación lineal de una función de varias variables

Si $P$ es un punto del dominio de una función de $n$ variables $f$ y $\mathbf{v}$ un vector en $\mathbb{R}^n$, la fórmula de Taylor de primer grado de $f$ alrededor del punto $P$ es

\[ f(P+\mathbf{v}) = f(P) + \nabla f(P)\cdot \mathbf{v} +R^1_{f,P}(\mathbf{v}), \]

donde

\[ P^1_{f,P}(\mathbf{v}) = f(P)+\nabla f(P)\mathbf{v} \]

es el polinomio de Taylor de primer grado de $f$ en el punto $P$, y $R^1_{f,P}(\mathbf{v})$ es el resto de taylor para el vector $\mathbf{v}$, y mide el error cometido en la aproximación.

Se cumple que

\[ \lim_{|\mathbf{v}|\rightarrow 0} \frac{R^1_{f,P}(\mathbf{v})}{|\mathbf{v}|} = 0 \]

Para una función de dos variables $f(x,y)$ y $P=(a, b)$, teniendo en cuenta que para un punto cualquiera $Q=(x,y)$, el vector $\mathbf{v}=\vec{PQ}=(x-a, y-b)$, el polinomio de Taylor de $f$ en el punto $P$, puede expresarse

\[\begin{align*} P^1_{f,P}(x,y) &= f(a,b)+\nabla f(a,b)(x-a,y-b) =\\ &= f(a,b)+\frac{\partial f}{\partial x}(a,b)(x-a)+\frac{\partial f}{\partial y}(a,b)(y-b), \end{align*}\]

que coincide con el plano tangente a $f$ en $(a,b)$.

Ejemplo 12.27 Dado el campo escalar $f(x,y)=\log(xy)$, su gradiente es

\[ \nabla f(x,y) = \left(\frac{1}{x},\frac{1}{y}\right), \]

y el polinomio de Taylor de primer grado en el punto $P=(1,1)$ es

\[\begin{align*} P^1_{f,P}(x,y) &= f(1,1) +\nabla f(1,1)\cdot (x-1,y-1) = \\ &= \log 1+(1,1)\cdot(x-1,y-1) = x-1+y-1 = x+y-2.\\ \end{align*}\]

Este polinomio, permite aproximar el valor de $f$ cerca del punto $P$.

Por ejemplo

\[ f(1.01,1.01) \approx P^1_{f,P}(1.01,1.01) = 1.01+1.01-2 = 0.02. \]

12.16.2 Aproximación cuadrática de una función de varias variables

Si $P$ es un punto del dominio de una función de $n$ variables $f$ y $\mathbf{v}$ un vector, la fórmula de Taylor de segundo grado de $f$ alrededor del punto $P$ es

\[ f(P+\mathbf{v}) = f(P) + \nabla f(P)\cdot \mathbf{v} + \frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v} + R^2_{f,P}(\mathbf{v}), \]

donde

\[ P^2_{f,P}(\mathbf{v}) = f(P)+\nabla f(P)\mathbf{v}+\frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v} \]

es el polinomio de Taylor de segundo grado de $f$ en el punto $P$, y $R^2_{f,P}(\mathbf{v})$ es el resto de taylor para el vector $\mathbf{v}$.

Se cumple que

\[ \lim_{|\mathbf{v}\rightarrow 0|} \frac{R^2_{f,P}(\mathbf{v})}{|\mathbf{v}|^2} = 0 \]

lo que indica que el resto es mucho más pequeño que el cuadrado del módulo de $\mathbf{v}$, y por tanto, la aproximación cuadrática es mejor que la lineal.

Si $f$ es un campo escalar de dos variables $f(x,y)$ y $P=(a, b)$, el polinomio de Taylor de $f$ en el punto $P$, puede expresarse

\[ \begin{gathered} P^2_{f,P}(x,y) = f(a,b)+\nabla f(a,b)(x-a,y-b) +\\ +\frac{1}{2}(x-a,y-b)\nabla^2f(a,b)(x-a,y-b)= \\ = f(a,b)+\frac{\partial f}{\partial x}(a,b)(x-a)+\frac{\partial f}{\partial y}(a,b)(y-b)+\\ +\frac{1}{2}\left(\frac{\partial^2 f}{\partial x^2}(a,b) (x-a)^2 + 2\frac{\partial^2 f}{\partial y\partial x}(a,b) (x-a)(y-b) + \frac{\partial^2 f}{\partial y^2}(a,b) (y-b)^2\right) \end{gathered} \]

Ejemplo 12.28 Dado el campo escalar $f(x,y)=\log(xy)$, su gradiente es

\[ \nabla f(x,y) = \left(\frac{1}{x},\frac{1}{y}\right), \]

y su matriz hessiana es

\[ \nabla ^2 f(x,y) = \left( \begin{array}{cc} \frac{-1}{x^2} & 0\\ 0 & \frac{-1}{y^2} \end{array} \right) \]

Por tanto, el polinomio de Taylor de segundo grado en el punto $P=(1,1)$ es

\[\begin{align*} P^2_{f,P}(x,y) &= f(1,1) +\nabla f(1,1)\cdot (x-1,y-1) + \frac{1}{2}(x-1,y-1)\nabla^2f(1,1)\cdot(x-1,y-1)=\\ &= \log 1+(1,1)\cdot(x-1,y-1) + \frac{1}{2}(x-1,y-1) \left( \begin{array}{cc} -1 & 0\\ 0 & -1 \end{array} \right) \left( \begin{array}{c} x-1\\ y-1 \end{array} \right) = \\ &= x-1+y-1+\frac{-x^2-y^2+2x+2y-2}{2} = \frac{-x^2-y^2+4x+4y-6}{2}. \end{align*}\]

Y la aproximación cuadrática en el mismo punto de antes es

\[ f(1.01,1.01) \approx P^1_{f,P}(1.01,1.01) = \frac{-1.01^2-1.01^2+4\cdot 1.01+4\cdot 1.01-6}{2} = 0.0199, \]

que es mejor que la aproximación lineal.