8 Integrales de funciones
\[ \newcommand{\mathbb{N}}{\mathbb{N}} \newcommand{\mathbb{Z}}{\mathbb{Z}} \newcommand{\mathbb{Q}}{\mathbb{Q}} \newcommand{\mathbb{R}}{\mathbb{R}} \newcommand{\mathbb{C}}{\mathbb{C}} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\Ext}{Ext} \DeclareMathOperator{\Fr}{Fr} \DeclareMathOperator{\Adh}{Adh} \DeclareMathOperator{\Ac}{Ac} \DeclareMathOperator{\sen}{sen} \]
En este capítulo se estudian las integrales de funciones de números reales, que junto a las derivadas son las dos ramas del Análisis más importantes. Veremos también el teorema fundamental del cálculo, uno de los resultados más importantes del Análisis que relaciona el cálculo diferencial con el integral, al cuál llegaron de manera simultanea Newton y Leibniz.
Históricamente el concepto de integral surge a partir del estudio de áreas, inicialmente de figuras geométricas, y después, de figuras curvas. En la antigua Grecia ya se utilizaba el método por agotamiento para calcular áreas de figuras no geométricas, y Arquímedes fue capaz de aproximar el área encerrada por una circunferencia usando este método.
Para llegar a la definición de integral explotaremos este método aproximando el area bajo una función usando rectángulos. El precursor de esta idea fue Bernhard Riemann.
8.1 Sumas de Riemann
Definición 8.1 (Partición de un intervalo) Dado un intervalo \(I=[a,b]\) cerrado y acotado en \(\mathbb{R}\), una partición de \(I\) es un conjunto ordenado y finito \(P=\{x_0, x_1, \ldots, x_n\}\) de puntos de \(I\) tales que \(a=x_0<x_1<x_2<\cdots<x_n=b\).
El conjunto de todas las particiones de un intervalo \(I\) se denota \(\mathcal{P}(I)\).
Definición 8.2 (Suma inferior de Riemann) Dada una función \(f: I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\) y una partición \(P=\{x_0, x_1, \ldots, x_n\}\) de \(I\), se define la suma inferior de \(f\) respecto de \(P\), y se denota \(s(f,P)\), como
\[ s(f,P) = \sum_{i=1}^n m_i(x_i-x_{i-1}) \]
donde \(m_i=\inf\{f(x): x\in[x_{i-1},x_i]\}\) para \(i=1,\ldots,n\).
Gráficamente, si \(f\) es una función positiva, la suma inferior se puede interpretar como la suma de las areas de los rectángulos con base \([x_{i-1},x_i]\) y altura \(m_i\).
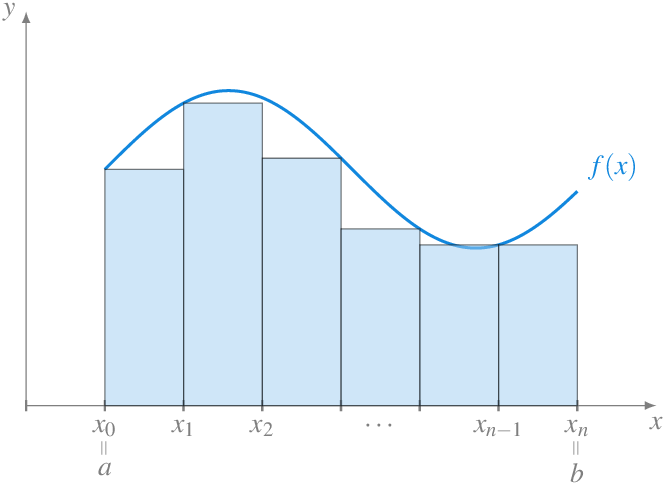
Definición 8.3 (Suma superior de Riemann) Dada una función \(f: I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\) y una partición \(P=\{x_0, x_1, \ldots, x_n\}\) de \(I\), se define la suma superior de \(f\) respecto de \(P\), y se denota \(S(f,P)\), como
\[ S(f,P) = \sum_{i=1}^n M_i(x_i-x_{i-1}) \]
donde \(M_i=\sup\{f(x): x\in[x_{i-1},x_i]\}\) para \(i=1,\ldots,n\).
Gráficamente, si \(f\) es una función positiva, la suma superior se puede interpretar como la suma de las areas de los rectángulos con base \([x_{i-1},x_i]\) y altura \(M_i\).
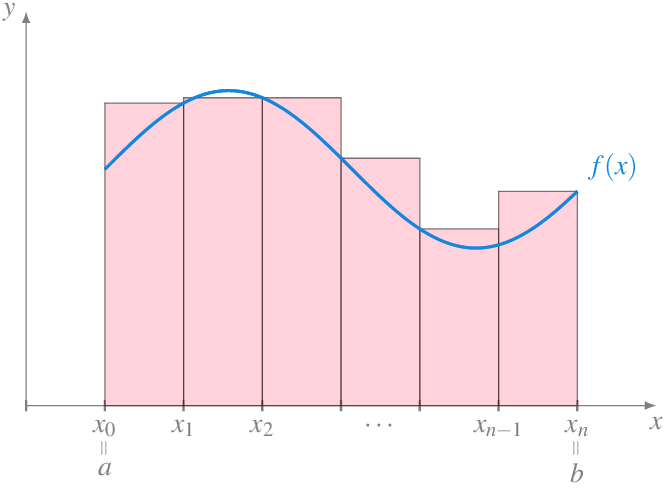
Obsérvese que si una función es negativa en un intervalo \(I\), sus sumas de Riemann son negativas, ya que las alturas de los rectángulos son negativas.
Ejemplo 8.1 Dada la función \(f(x)=x^2\), si consideramos el intervalo \([0,2]\) y la partición \(P=\{0, 0.5, 1, 1.5, 2\}\), la suma inferior de Riemann de \(f\) correspondiente a esta partición es
\[\begin{align*} s(f,P) &= f(0)(0.5-0) + f(0.5) (1-0.5) + f(1) (1.5-1) + f(1.5) (2-1.5) \tag{1}\\ &= 0\cdot 0.5 + 0.5^2\cdot 0.5 + 1^2 \cdot 0.5 + 1.5^2 \cdot 0.5 = 1.75 \end{align*}\] (1) Como \(f\) es creciente, el ínfimo en cada intervalo se alcanza en el extremo inferior.
Y la suma superior es
\[\begin{align*} s(f,P) &= f(0.5)(0.5-0) + f(1) (1-0.5) + f(1.5) (1.5-1) + f(2) (2-1.5) \tag{2}\\ &= 0.5\cdot 0.5 + 1^2\cdot 0.5 + 1.5^2 \cdot 0.5 + 2^2 \cdot 0.5 = 3.75 \end{align*}\] (2) Como \(f\) es creciente, el supremo en cada intervalo se alcanza en el extremo superior.
Calculadora de sumas de Riemann
Proposición 8.1 Si \(f:I\to\mathbb{R}\) es una función acotada en el intervalo \(I=[a,b]\) y \(P=\{x_0, x_1, \cdots, x_n\}\) es una partición de \(I\), entonces \(s(f,P)\leq S(f,P)\).
Prueba. Para cada \(i=1,\ldots,n\) se tiene que
\[ m_i=\inf\{f(x): x\in[x_{i-1},x_i]\}\leq \sup\{f(x): x\in[x_{i-1},x_i]\} = M_i, \]
de manera que
\[ s(f,P) = \sum_{i=1}^n m_i(x_i-x_{i-1}) \leq \sum_{i=1}^n M_i(x_i-x_{i-1}) = S(f,P), \]
ya que \((x_i-x_{i-1})>0\) \(\forall i=1,\ldots,n\).
Definición 8.4 (Refinamiento de una partición) Dadas dos particiones \(P=\{x_0, x_1, \ldots, x_n\}\) y \(Q=\{y_0, y_1, \ldots, y_m\}\) de un intervalo \(I=[a,b]\), se dice que \(Q\) es un refinamiento de \(P\) si todos los puntos de \(P\) están en \(Q\), es decir, \(P\subseteq Q\).
Proposición 8.2 Si \(f:I\to\mathbb{R}\) es una función acotada en el intervalo \(I=[a,b]\), \(P\) es una partición de \(I\) y \(Q\) es un refinamiento de \(P\), entonces
- \(s(f,P)\leq s(f,Q)\)
- \(S(f,Q)\leq S(f,P)\)
Prueba. Veremos solo la prueba para las sumas inferiores.
Probaremos primero el resultado para un refinamiento con un punto más. Sea \(P=\{x_0, x_1, \cdots, x_n\}\) y supongamos que \(Q\) solo tiene un punto \(c\) más que \(P\). Sea \(k\in\{1,\ldots,n\}\) tal que \(c\in[x_{k-1},x_k]\) y tomemos \(m_k'=\inf\{f(x): x\in[x_{k-1},c]\}\) y \(m_k''=\inf\{f(x): x\in[c,x_k]\}\). Como \(m_k=\inf\{f(x): x\in[x_{k-1},x_k]\}\) resulta evidente que \(m_k\leq m_k'\) y \(m_k\leq m_k''\), por lo que
\[ m_k(x_k-x_{k-1}) = m_k(x_k-c)+m_k(c-x_{k-1})\leq m_k''(x_k-c)+m_k'(c-x_{k-1}) \]
y entonces
\[\begin{align*} s(f,P) &= \sum_{i=1}^n m_i(x_i-x_{i-1}) = \sum_{i=1,i\neq k}^n m_i(x_i-x_{i-1}) + m_k(x_k-x_{k-1}) \\ &\leq \sum_{i=1,i\neq k}^n m_i(x_i-x_{i-1}) + m_k''(x_k-c) + m_k'(c-x_{k-1}) = s(f,Q). \end{align*}\]
Para probar el caso general, si \(Q\) es un refinamiento cualquiera de \(P\), entonces existe una sucesión finita de particiones de \(I\), \(P_1,P_2,\ldots,P_r\) tales que \(P=P_1\subset P_2\subset\cdots \subset P_r=Q\) y cada \(P_i\) tiene solo un punto más que \(P_{i-1}\). Así pues, por el resultado anterior,
\[ s(f,P)\leq s(f,P_2)\leq \cdots \leq s(f,Q). \]
La prueba para las sumas superiores es análoga y se deja como ejercicio.
Proposición 8.3 Si \(f:I\to\mathbb{R}\) es una función acotada en el intervalo \(I=[a,b]\) y \(P\) y \(Q\) son dos particiones de \(I\), entonces \(s(f,P)\leq S(f,Q)\) y \(s(f,Q)\leq S(f,P)\).
Prueba. Tomando la partición de \(I\) \(P'=P\cup Q\), se tiene que \(P'\) es un refinamiento de \(P\) y \(Q\), de manera que, según las proposiciones anteriores se tiene
\[ s(f,P)\leq s(f,P')\leq S(f,P')\leq S(f,Q) \]
y
\[ s(f,Q)\leq s(f,P')\leq S(f,P')\leq S(f,P). \]
8.2 Integrales de Riemann
Como acabamos de ver, dada una función \(f\) positiva en un intervalo \(I\), para cualquier partición \(P\) de \(I\), la suma inferior de Riemann es una aproximación por defecto del área encerrada entre la gráfica de \(f\) y el eje \(x\) en el intervalo \(I\), mientras que la suma superior de Riemann es una aproximación por exceso. Si al hacer refinamientos de la partición \(P\), cada vez con un mayor número de subintervalos, las sumas inferiores crecen y las superiores decrecen, se obtienen aproximaciones cada vez mejores. Podemos explotar esta idea para calcular el area área encerrada entre la gráfica de \(f\) y el eje \(x\) tomando particiones con subintervalos cada vez más pequeños.
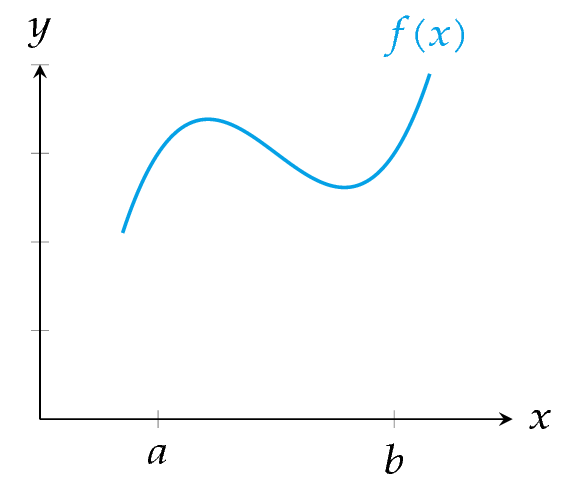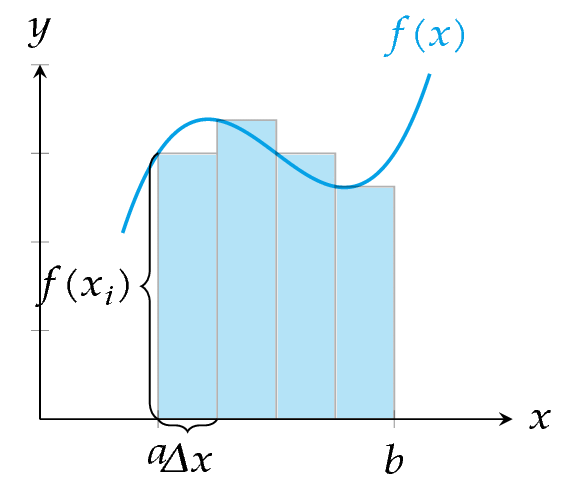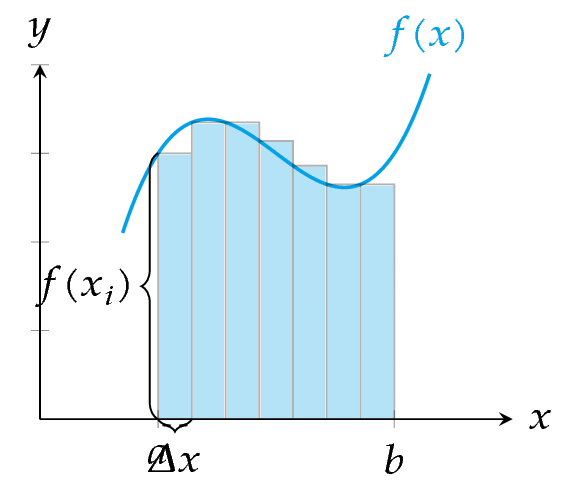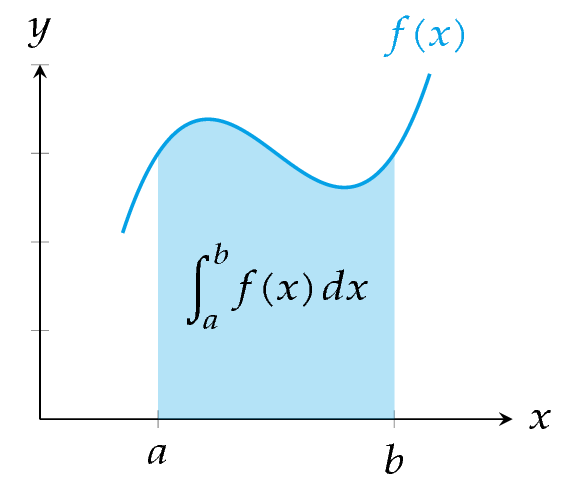
Definición 8.5 (Integral inferior de Riemann) Dada una función \(f:I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\), se define la integral inferior de \(f\) en \(I\) como el número \(\underline{\int_a^b} f =\sup\{s(f,P): P\in \mathcal{P}(I)\}\).
Definición 8.6 (Integral superior de Riemann) Dada una función \(f:I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\), se define la integral superior de \(f\) en \(I\) como el número \(\overline{\int_a^b} f =\inf\{S(f,P): P\in \mathcal{P}(I)\}\).
Proposición 8.4 Si \(f:I\to\mathbb{R}\) es una función acotada en el intervalo \(I=[a,b]\), entonces \(\underline{\int_a^b} f\leq \overline{\int_a^b}f\).
Prueba. Sean \(P\) y \(Q\) dos particiones cualesquiera de \(I\). Por la proposición anterior, \(s(f,P)\leq S(f,Q)\) \(\forall P\in\mathcal(P)(I)\), de modo que \(S(f,Q)\) es una cota superior de todas las sumas inferiores, y por tanto,
\[ \underline{\int_a^b} f = \sup\{s(f,P): P\in\mathcal{P}(I)\}\leq S(f,Q) \]
Como esto es cierto para cualquier partición \(Q\), se tiene que \(\underline{\int_a^b} f\) es una cota inferior de todas las sumas superiores, y por tanto,
\[ \underline{\int_a^b} f \leq \inf\{S(f,Q): Q\in\mathcal{P}(I)\} = \overline{\int_a^b}f. \]
Definición 8.7 (Integral de Riemann) Dada una función \(f:I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\), se dice que \(f\) es integrable Riemann en \(I\) si
\[ \underline{\int_a^b} f = \overline{\int_a^b}f, \]
y a este valor se le llama integral de Riemann o integral definida de \(f\) en \(I\) y se denota por \(\int_a^b f\), o bien
\[ \int_a^b f(x)\,dx \]
Si \(f\) es integrable Riemann en \(I\), el número \(\int_a^b f(x)\,dx\) es el único número real que verifica \(s(f,P)\leq \int_a^b f(x)\,dx\leq S(f,P)\) \(\forall P\in\mathcal{P}(I)\).
En ocasiones, omitiremos el “de Riemann” para referirnos a una integral de Riemann y simplemente se escribirá integral, cuando en el contexto esté claro que se trata de la integral de Riemann.
Ejemplo 8.2
Veamos que si \(f(x)=c\), es una función constante en \(I=[a,b]\), entonces \(f\) es integrable en \(I\).
Sea \(P=\{x_0, x_1, \ldots, x_n\}\) una partición de \([a,b]\), entonces
\[\begin{align*} s(f,P) &= \sum_{i=1}^n m_i(x_i-x_{i-1}) = \sum_{i=1}^n c(x_i-x_{i-1}) \\ &= c\sum_{i=1}^n (x_i-x_{i-1}) = c(x_n-x_0) = c(b-a). \end{align*}\]
Del mismo modo,
\[\begin{align*} S(f,P) &= \sum_{i=1}^n M_i(x_i-x_{i-1}) = \sum_{i=1}^n c(x_i-x_{i-1})\\ & = c\sum_{i=1}^n (x_i-x_{i-1}) = c(x_n-x_0) = c(b-a). \end{align*}\]
Así pues, \(s(f,P) = S(f,P)=c(b-a)\) \(\forall P\in\mathcal{P}(I)\) y \(\int_a^b f(x)\,dx = c(b-a)\).
Veamos que \(f(x)=x\) es integrable en \([0,1]\).
Sea \(P_n=\{0, \frac{1}{n}, \frac{2}{n}, \ldots, \frac{n}{n}\}\) una partición de \([0,1]\). Vamos a probar primero que \(\sup\{s(f,P_n):n\in\mathbb{N}\} = \inf\{S(f,P_n):n\in\mathbb{N}\}\). Como \(f\) es creciente y continua en \([0,1]\), se cumple que
\[\begin{align*} m_i &= \inf\{f(x): x\in[x_{i-1},x_i]\} = f(x_{i-1}),\\ M_i &= \sup\{f(x): x\in[x_{i-1},x_i]\} = f(x_i), \end{align*}\]
y por tanto,
\[\begin{align*} s(f,P_n) &= \sum_{i=1}^n m_i\left(\frac{i}{n}-\frac{i-1}{n}\right) = \sum_{i=1}^n f\left(\frac{i-1}{n}\right)\frac{1}{n} = \sum_{i=1}^n \frac{i-1}{n}\frac{1}{n}\\ & = \frac{1}{n^2}\sum_{i=1}^n (i-1) =\frac{1}{n^2}\frac{(n-1)n}{2} = \frac{1}{2}\left(1-\frac{1}{n}\right),\\ S(f,P_n) &= \sum_{i=1}^n M_i\left(\frac{i}{n}-\frac{i-1}{n}\right) = \sum_{i=1}^n f\left(\frac{i}{n}\right)\frac{1}{n} = \sum_{i=1}^n \frac{i}{n}\frac{1}{n}\\ & = \frac{1}{n^2}\sum_{i=1}^n i =\frac{1}{n^2}\frac{n(n+1)}{2} = \frac{1}{2}\left(1+\frac{1}{n}\right).\\ \end{align*}\]
Así pues,
\[ \begin{gathered} \sup\{s(f,P_n):n\in\mathbb{N}\} = \sup\left\{\frac{1}{2}\left(1-\frac{1}{n}\right):n\in\mathbb{N}\right\} =\frac{1}{2} \\ = \inf\left\{\frac{1}{2}\left(1+\frac{1}{n}\right):n\in\mathbb{N}\right\} = \inf\{S(f,P_n):n\in\mathbb{N}\} \end{gathered} \]
Ahora bien, como
\[ \begin{gathered} \sup\{s(f,P_n):n\in\mathbb{N}\}\leq \sup\{s(f,P):P\in\mathcal{P}(I)\} = \underline{\int_0^1} f \\ \leq \overline{\int_0^1} f =\inf\{S(f,P):P\in\mathcal{P}(I)\} \leq \inf\{S(f,P_n):n\in\mathbb{N}\} \end{gathered} \]
se puede concluir que \(\underline{\int_0^1} f = \overline{\int_0^1} f\), y por tanto \(\int_0^1 f(x)\, dx = \frac{1}{2}\).
Ejemplo 8.3 La función
\[ f(x) = \begin{cases} 1 & \mbox{si } x\in\mathbb{Q}\cap[0,1]\\ 0 & \mbox{si } x\in\mathbb{R}\setminus\mathbb{Q}\cap[0,1] \end{cases} \]
no es integrable Riemann ya que para cualquier partición \(P=\{x_0, x_1, \ldots, x_n\}\) del intervalo \([0,1]\) se tiene que
\[\begin{align*} m_i &= \inf\{f(x): x\in [x_{i-1},x_i]\} = 0,\\ M_i &= \sup\{f(x): x\in [x_{i-1},x_i]\} = 1, \end{align*}\]
por lo que \(s(f,P)=0\) y \(S(f,P)=1\) \(\forall P\in\mathcal{P}([0,1])\).
Así pues, \(\underline{\int_a^b}f = 0 \neq \overline{\int_a^b}f=1\).
Teorema 8.1 (Criterio de integrabilidad de Riemann) Una función \(f:I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\) es integrable en \(I\) si y sólo si para cada \(\varepsilon>0\) existe una partición \(P\in\mathcal{P}(I)\) tal que \(S(f,P)-s(f,P)<\varepsilon\).
Prueba. Supongamos que \(f\) es integrable Riemann en \(I\), es decir, \(\underline{\int_a^b}f = \overline{\int_a^b}f\). Dado \(\varepsilon>0\) existe \(P_1\in\mathcal{P}(I)\) tal que \(\underline{\int_a^b} f-\frac{\varepsilon}{2}\leq s(f,P_1)\) por ser \(\underline{\int_a^b} f =\sup\{s(f,P): P\in \mathcal{P}(I)\}\).
Del mismo modo, por ser \(\overline{\int_a^b} f =\inf\{S(f,P): P\in \mathcal{P}(I)\}\), existe una partición \(P_2\in\mathcal{P}(I)\) tal que \(\overline{\int_a^b} f+\frac{\varepsilon}{2} \geq S(f,P_2)\).
Tomando \(P = P_1\cup P_2\), se tiene que \(s(f,P_1)\leq s(f,P)\) y \(S(f,P)\leq S(f,P_2)\). Así pues,
\[ S(f,P)-s(f,P) \leq S(f,P_2)-s(f,P_1) \leq \left(\overline{\int_a^b} f+\frac{\varepsilon}{2}\right) - \left(\underline{\int_a^b} f-\frac{\varepsilon}{2}\right) = \varepsilon. \]
Para probar el otro sentido de la implicación, supongamos que para cada \(\varepsilon>0\) existe una partición \(P\in\mathcal{P}(I)\) tal que \(S(f,P)-s(f,P)<\varepsilon\). Entonces,
\[ 0\leq \overline{\int_a^b} f- \underline{\int_a^b} f \leq S(f,P)-s(f,P)<\varepsilon, \]
y como esto es cierto para cualquier \(\varepsilon>0\), se tiene \(\overline{\int_a^b} f=\underline{\int_a^b} f\) y \(f\) es integrable Riemann.
Corolario 8.1 Dada una función \(f:I\to\mathbb{R}\) acotada en el intervalo \(I=[a,b]\), si existe una sucesión de particiones \((P_n)_{n=1}^\infty\) de \(I\) tal que \(\lim_{n\to\infty} S(f,P_n)-s(f,P_n) =0\), entonces \(f\) es integrable Riemann en \(I\) y
\[ \int_a^b f(x)\,dx = \lim_{n\to\infty} s(f,P_n) = \lim_{n\to\infty} S(f,P_n). \]
Prueba. Dado \(\varepsilon>0\), como \(\lim_{n\to\infty} S(f,P_n)-s(f,P_n) =0\), existe \(k\in\mathbb{N}\) tal que \(S(f,P_k)=s(f,P_k)<\varepsilon\), luego, por el criterio de integrabilidad de Riemann, se tiene que \(f\) es integrable en \(I\).
Para calcular el valor de la integral, se tiene
\[ \begin{gathered} \lim_{n\to\infty} s(f,P_n) \leq \sup\{s(f,P):n\in\mathbb{N}\} \leq \sup\{s(f,P): P\in \mathcal{P}(I)\} = \int_a^b f(x)\, dx \\ = \inf\{S(f,P): P\in\mathcal{P}(I)\} \leq \inf\{S(f,P_n): n\in\mathbb{N}\} \leq \lim_{n\to\infty} S(f,P_n), \end{gathered} \]
y como \(\lim_{n\to\infty} s(f,P_n) = \lim_{n\to\infty} S(f,P_n)\), las desigualdades anteriores se convierten en igualdades y por tanto,
\[ \int_a^b f(x)\,dx = \lim_{n\to\infty} s(f,P_n) = \lim_{n\to\infty} S(f,P_n). \]
Este último resultado nos permite calcular una integral como el límite de las sumas de Riemann tomando una sucesión de particiones cada vez más refinada.
8.3 Propiedades de la integral de Riemann
Teorema 8.2 Si \(f,g:I\to\mathbb{R}\) son dos funciones integrables Riemann en \(I=[a,b]\), entonces
\(f+g\) es integrable Riemann en \(I\) y \(\int_a^b (f+g)(x)\, dx = \int_a^b f(x)\,dx + \int_a^b g(x)\,dx.\)
Para cualquier \(c\in\mathbb{R}\), \(cf\) es integrable Riemann en \(I\) y \(\int_a^b cf(x)\, dx = c\int_a^b f(x)\,dx.\)
Prueba. Veamos la demostración de cada apartado.
En primer lugar, resulta sencillo ver que para cualquier subintervalo \(J\) de \(I\) se cumple
\[ \begin{gathered} \inf\{(f+g)(x): x\in J\} \geq \inf\{f(x): x\in J\} + \inf\{g(x): x\in J\}\\ \sup\{(f+g)(x): x\in J\} \leq \sup\{f(x): x\in J\} + \sup\{g(x): x\in J\} \end{gathered} \tag{8.1}\]
Dado \(\varepsilon>0\), como \(f\) y \(g\) son integrables, existen dos particiones \(P_1,P_2\in \mathcal{P}(I)\) tales que
\[ \begin{gathered} S(f,P_1)-s(f,P_1)\leq \frac{\varepsilon}{2}\\ S(g,P_2)-s(g,P_2)\leq \frac{\varepsilon}{2} \end{gathered} \]
Tomando ahora el refinamiento \(P=P_1\cup P_2\) de \(P_1\) y \(P_2\) y la Ecuación 8.1 se tiene
\[\begin{align*} s(f+g,P) &\geq s(f,P) + s(g,P) \geq s(f,P_1) + s(g,P_2)\\ S(f+g,P) &\leq S(f,P) + S(g,P) \leq S(f,P_1) + S(g,P_2) \end{align*}\]
de manera que
\[\begin{align*} S(f+g,P)-s(f+g,P) &\leq (S(f,P_1)+S(g,P_2))-(s(f,P_ 1)+s(g,P_2)) \\ &\leq \frac{\varepsilon}{2}+\frac{\varepsilon}{2} =\varepsilon. \end{align*}\]
Y, por tanto, \(f+g\) es integrable Riemann en \(I\).
Además,
\[ s(f,P) + s(g,P) \leq s(f+g,P) \leq \int_a^b (f+g) \leq S(f+g,P) \leq S(f,P) + S(g,P) \]
y
\[ s(f,P) + s(g,P) \leq \int_a^b f + \int_a^b g \leq S(f,P) + S(g,P), \]
por lo que se tiene
\[ 0\leq \left|\int_a^b (f+g) - \left(\int_a^b f + \int_a^b g\right)\right| \leq (S(f,P)+S(g,P)) - (s(f,P)+s(g,P)) \leq \varepsilon, \]
y por consiguiente, \(\int_a^b (f+g) = \int_a^b f + \int_a^b g\).
Si \(c=0\) entonces \(cf=0\), y por tanto, \(cf\) es integrable y además \(\int_a^b cf = 0 = c\int_a^b f\).
Supongamos ahora que \(c>0\). Resulta sencillo ver que para cualquier subintervalo \(J\) de \(I\) se cumple
\[ \begin{gathered} \inf\{(cf)(x): x\in J\} = c\inf\{f(x): x\in J\}\\ \sup\{(cf)(x): x\in J\} = c\sup\{f(x): x\in J\} \end{gathered} \tag{8.2}\]
de manera que si \(P\) es una partición de \(I\), entonces \(s(cf,P)= cs(f,P)\) y \(S(cf,P) = cS(f,P)\).
Como \(f\) es integrable Riemann, dado \(\varepsilon>0\) existe una partición \(P\in\mathcal{P}(I)\) tal que \(S(f,P)-s(f,P)\leq \frac{\varepsilon}{c} >0\). Por otro lado, según la Ecuación 8.2,
\[ S(cf,P) - s(cf,P) = c S(f,P) - cs(f,P) = c(S(f,P)-s(f,P)) < c\frac{\varepsilon}{c} = \varepsilon, \]
de manera que \(cf\) es integrable en \(I\), y además,
\[\begin{align*} \int_a^b cf &= \inf\{S(cf,P): P\in \mathcal{P}(I)\} = \inf\{cS(f,P): P\in \mathcal{P}(I)\} \\ &= c\inf\{S(f,P): P\in \mathcal{P}(I)\} = c\int_a^b f. \end{align*}\]
Finalmente, si \(c<0\), resulta sencillo ver que para cualquier subintervalo \(J\) de \(I\) se cumple
\[ \begin{gathered} \inf\{(cf)(x): x\in J\} = c\sup\{f(x): x\in J\}\\ \sup\{(cf)(x): x\in J\} = c\inf\{f(x): x\in J\} \end{gathered} \tag{8.3}\]
de manera que si \(P\) es una partición de \(I\), entonces \(s(cf,P)= cS(f,P)\) y \(S(cf,P) = cs(f,P)\).
Como \(f\) es integrable Riemann, dado \(\varepsilon>0\) existe una partición \(P\in\mathcal{P}(I)\) tal que \(S(f,P)-s(f,P)\leq \frac{\varepsilon}{-c} >0\). Por otro lado, según la Ecuación 8.3,
\[\begin{align*} S(cf,P) - s(cf,P) &= c s(f,P) - cS(f,P) = c(s(f,P)-S(f,P)) \\ &= c(S(f,P)-s(f,P)) < -c\frac{\varepsilon}{-c} = \varepsilon, \end{align*}\]
de manera que \(cf\) es integrable en \(I\), y además,
\[\begin{align*} \int_a^b cf &= \inf\{S(cf,P): P\in \mathcal{P}(I)\} = \inf\{cs(f,P): P\in \mathcal{P}(I)\} \\ &= c\sup\{s(f,P): P\in \mathcal{P}(I)\} = c\int_a^b f. \end{align*}\]
Proposición 8.5 Si \(f:I\to\mathbb{R}\) es una función integrable Riemann en \(I=[a,b]\) y \(f(x)\geq 0\) \(\forall x\in I\), entonces \(\int_a^b f(x)\,dx \geq 0\).
Prueba. Para cualquier partición \(P\in\mathcal{P}(I)\) se tiene que \(f(x)\) es positiva en cualquier intervalo de la partición y por tanto \(s(f,P)\geq 0\). Así pues, \(\int_a^b f(x)\,dx = \sup\{s(f,P):P\in \mathcal{P}(I)\}\geq 0\).
Corolario 8.2 Si \(f:I\to\mathbb{R}\) es una función integrable Riemann en \(I=[a,b]\) y \(f(x)\leq 0\) \(\forall x\in I\), entonces \(\int_a^b f(x)\,dx \leq 0\).
Prueba. Consideremos la función \(-f(x)\geq 0\) \(\forall x\in\mathbb{R}\). Como \(f\) es integrable en \(I\), también lo es \((-1)f\) y
\[ \int_a^b f(x)\, dx = \int_a^b (-1)(-f(x))\,dx = - \int_a^b -f(x)\,dx \leq 0, \]
ya que por la proposición anterior \(\int_a^b -f(x)\,dx \geq 0\).
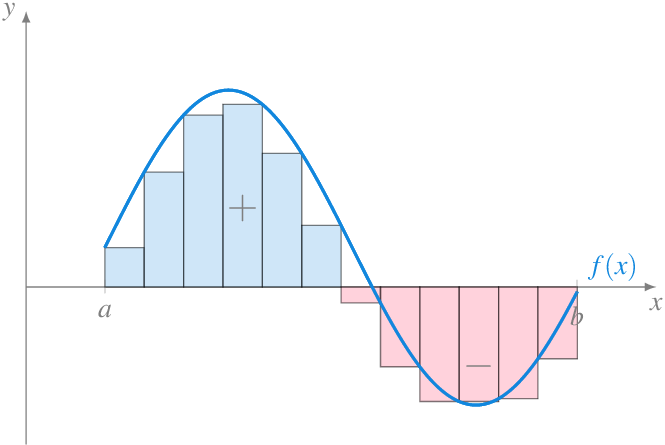
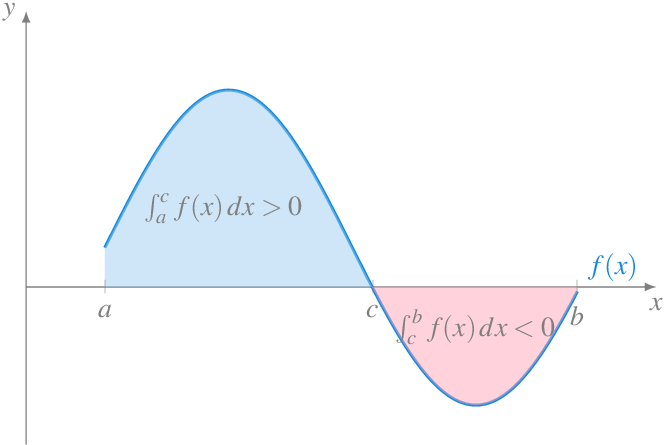
Este resultado nos advierte de que no se puede utilizar directamente la integral de Riemann para calcular el area entre la gráfica de la función y el eje \(x\) si la función presenta valores negativos en el intervalo de integración \(I\).
En estos casos, el recurso habitual para calcular el área es calcular la integral del valor absoluto de la función.
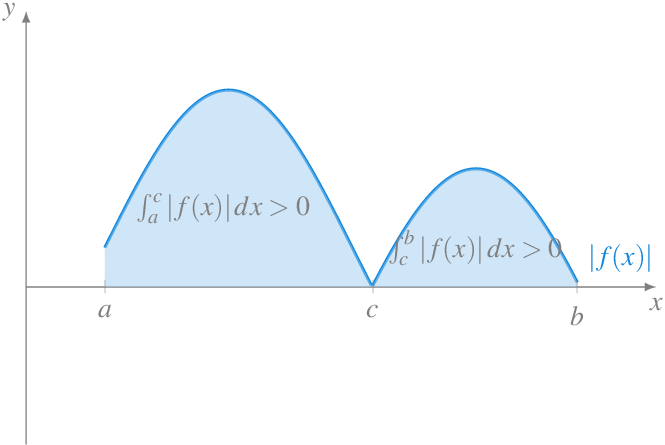
Corolario 8.3 Si \(f,g:I\to\mathbb{R}\) son dos funciones integrables Riemann en \(I=[a,b]\) y \(f(x)\leq g(x)\) \(\forall x\in I\), entonces \(\int_a^b f(x)\,dx \leq \int_a^b g(x)\,dx\).
Prueba. Consideremos la función \(g(x)-f(x)\geq 0\) \(\forall x\in\mathbb{R}\). Como \(f\) y \(g\) son integrables en \(I\), también lo es \(g-f\) y
\[ \int_a^b g(x)-f(x)\, dx = \int_a^b g(x)\,dx - \int_a^b f(x)\,dx \geq 0 \Rightarrow \int_a^b f(x)\,dx \leq \int_a^b g(x)\,dx. \]
Corolario 8.4 Si \(f:I\to\mathbb{R}\) es una función integrable Riemann en \(I=[a,b]\) y \(m\leq f(x)\leq M\) \(\forall x\in I\), entonces \(m(b-a)\leq \int_a^b f(x)\,dx \leq M(b-a)\).
Prueba. Por el corolario anterior se tiene \(\int_a^b m\,dx \leq \int_a^b f(x)\,dx \leq \int_a^b M\,dx\).
Por otro lado, como \(\int_a^b m\,dx = m(b-a)\) y \(\int_a^b M\,dx = M(b-a)\) por tratarse de funciones constantes, sustituyendo en la desigualdad anterior se tiene
\[ m(b-a)\leq \int_a^b f(x)\,dx \leq M(b-a). \]
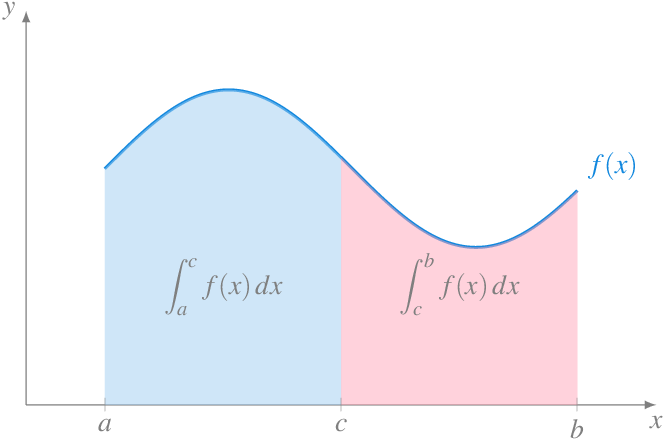
Teorema 8.3 (Aditividad de la integral respecto del intervalo de integración) Si \(f:I\to\mathbb{R}\) es una función acotada en \(I=[a,b]\) y \(c\in(a,b)\), entonces \(f\) es integrable Riemann en \(I\) si y sólo si \(f\) es integrable Riemann en \([a,c]\) y \([c,b]\). Además, en este caso,
\[ \int_a^b f(x)\,dx = \int_a^c f(x)\,dx + \int_c^b f(x)\,dx \]
Prueba. Supongamos que \(f\) es integrable en \(I\). Entonces, dado \(\varepsilon>0\), existe \(P\in\mathcal{P}(I)\) tal que \(S(f,P)-s(f,P)<\varepsilon\).
Sea \(Q=P\cup\{c\}\in\mathcal{P}(I)\). Como \(Q\) es un refinamiento de \(P\), se cumple
\[ S(f,Q)-s(f,Q) \leq S(f,P)-s(f,P) \leq \varepsilon \]
Tomando ahora las subparticiones \(Q_1=\{t\in Q:t\leq c\}\) y \(Q_2=\{t\in Q: t\geq c\}\), se tiene que
\[ \begin{gathered} (S(f,Q_1)-s(f,Q_1)) + (S(f,Q_2)-s(f,Q_2)) \\ = (S(f,Q_1) + S(f,Q_2)) - (s(f,Q_1) + s(f,Q_2)) \\ = S(f,P) - s(f,P) \leq S(f,Q) - s(f,Q) < \varepsilon, \end{gathered} \]
de manera que \(S(f,Q_1)-s(f,Q_1)<\varepsilon\) y \(S(f,Q_2)-s(f,Q_2)<\varepsilon\), y por tanto, \(f\) es integrable en \([a,c]\) y en \([c,b]\). Además,
\[ s(f,Q) = s(f,Q_1) + s(f,Q_2) \leq \int_a^c f + \int_c^b f \leq S(f,Q_1) + S(f,Q_2) = S(f,Q) \]
para cualquier \(Q\in\mathcal{P}(I)\) y \(c\in Q\). Si \(P\in\mathcal{P}(I)\), tomando \(Q=P\cup \{c\}\), \(Q\) es un refinamiento de \(P\), y por tanto,
\[ \begin{gathered} s(f,P) \leq s(f,Q) = s(f,Q_1) + s(f,Q_2) \leq \int_a^c f + \int_c^b f \\ \leq S(f,Q_1) + S(f,Q_2) = S(f,Q) \leq S(f,P), \end{gathered} \]
por lo que se concluye que \(\int_a^b f = \int_a^c f + \int_c^b f\).
Para probar el otro sentido de la implicación, supongamos que \(f\) es integrable en \([a,c]\) y \([c,b]\). Dado \(\varepsilon>0\) existe \(P_1\in\mathcal{P}([a,c])\) tal que \(S(f,P_1)-s(f,P_1)<\frac{\varepsilon}{2}\) y existe \(P_2\in\mathcal{P}([c,b])\) tal que \(S(f,P_2)-s(f,P_2)<\frac{\varepsilon}{2}\).
Tomando ahora \(P=P_1\cup P_2\in \mathcal{P}(I)\), se cumple
\[ S(f,P)-s(f,P) = s(f,P_1) + S(f,P_2) - (s(f,P_1) + s(f,P_2)) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} =\varepsilon, \]
por lo que \(f\) es integrable en \(I\).
A pesar de que la demostración es bastante larga, cuando \(f\) es positiva, es obvio que el área entre la gráfica de \(f\) y el eje \(x\) en el intervalo \([a,b]\) puede descomponerse en la suma de las áreas en los intervalos \([a,c]\) y \([c,b]\) para cualquier \(c\in(a,b)\).
8.4 Clase de las funciones integrables
A continuación trataremos de estudiar qué tipo de funciones son integrables.
Teorema 8.4 Si \(f:I\to\mathbb{R}\) es una función acotada y monótona en \(I=[a,b]\), entonces \(f\) es integrable en \(I\).
Prueba. Supongamos que \(f\) es creciente en \(I\). Dado \(\varepsilon>0\) existe un \(n\in\mathbb{N}\) tal que
\[ \frac{(f(b)-f(a))(b-a)}{n} < \varepsilon. \]
Sea ahora \(P_n\in\mathcal{P}(I)\) la partición que divide \(I\) en \(n\) subintervalos de igual longitud, es decir, \(P=\{x_0, x_1, \ldots, x_n\}\) con \(x_i = a+\frac{(b-a)i}{n}\).
Como \(f\) es creciente en \(I\) se tiene
\[\begin{align*} m_i &= \inf\{f(x): x\in[x_{i-1},x_i]\} = f(x_{i-1})\\ M_i &= \sup\{f(x): x\in[x_{i-1},x_i]\} = f(x_{i}) \end{align*}\] para \(i=1,\ldots,n\), de manera que
\[\begin{align*} S(f,P_n)-s(f,P_n) &= \sum_{i=1}^n f(x_i)(x_i-x_{i-1}) - \sum_{i=1}^n f(x_{i-1})(x_i-x_{i-1}) \\ &= \sum_{i=1}^n (f(x_i)-f(x_{i-1}))\frac{b-a}{n} \\ &= \frac{b-a}{n}(f(x_1)-f(x_0))+(f(x_2)-f(x_1))+ \cdots \\ & \cdots + (f(x_{n-1})-f(x_{n-2})+ (f(x_n)-f(x_{n-1}))) \\ &= \frac{b-a}{n}(f(b)-f(a)) < \varepsilon. \end{align*}\]
Así pues, \(f\) es integrable en \(I\).
Teorema 8.5 Si \(f:I\to\mathbb{R}\) es una función continua en \(I=[a,b]\), entonces \(f\) es integrable en \(I\).
Prueba. Observemos primero que como \(f\) es continua en \(I\), entonces es uniformemente continua en \(I\) al ser \(I\) un intervalo cerrado.
Dado \(\varepsilon>0\), como \(f\) es uniformemente continua en \(I\), para \(\varepsilon'=\frac{\varepsilon}{b-a}>0\) existe \(\delta>0\) tal que si \(|x-y|<\delta\) entonces \(|f(x)-f(y)|<\varepsilon'\).
Sea \(P=\{x_0,x_1,\ldots,x_n\}\) una partición que divide \(I\) en subintervalos de longitud menor que \(\delta\). Entonces, para cad \(i=1,\ldots, n\) se tiene
\[ M_i-m_i = \sup\{|f(x)-f(y)|: x,y\in[x_{i-1},x_i]\} \leq \varepsilon', \]
y por tanto,
\[\begin{align*} S(f,P)-s(f,P) &= \sum_{i=1}^n M_i(x_i-x_{i-1}) - \sum_{i=1}^n m_i(x_i-x_{i-1}) \\ &= \sum_{i=1}^n (M_i-m_i)(x_i-x_{i-1})\\ & < \varepsilon' \sum_{i=1}^n (x_i-x_{i-1}) = \varepsilon' (b-a) = \varepsilon. \end{align*}\]
Teorema 8.6 Si \(f:I\to\mathbb{R}\) es una función continua en \(I=[a,b]\), salvo en un punto \(c\in I\), entonces \(f\) es integrable en \(I\).
Prueba. Se deja como ejercicio.
Corolario 8.5 Si \(f:I\to\mathbb{R}\) es una función continua en \(I=[a,b]\), salvo en un conjunto finito de puntos de \(I\), entonces \(f\) es integrable en \(I\).
Prueba. Haremos la prueba por inducción sobre el número de puntos de discontinuidad.
El caso para un solo punto de discontinuidad se ha probado en el teorema anterior. Supongamos que si \(f\) tiene \(n\) puntos de discontinuidad en \(I\) entonces es integrable Riemann en \(I\), y supongamos ahora que \(f\) tiene \(n+1\) puntos de discontinuidad. Sea \(c\) el mayor de los puntos de discontinuidad. Tomando \(\delta>0\) se tiene que \(f\) tiene \(n\) puntos de discontinuidad en el intervalo \([a, c-\delta]\), por lo que es integrable en este intervalo.
Sea ahora \(\varepsilon>0\). Como \(f\) es integrable en \([a,c-\delta]\) existe una partición \(P_1\) de \([a,c-\delta]\) tal que \(S(f,P_1)-s(f,P_2)<\frac{\varepsilon}{2}\). Por otro lado, \(f\) está acotada en el intervalo \([c-\delta, b]\) y solo tiene una discontinuidad, por el teorema anterior, \(f\) es integrable en \([c-\delta,b]\), por lo que existe otra partición \(P_2\) de \([c-\delta,b]\) tal que \(S(f,P_2)-s(f,P_2)<\frac{\varepsilon}{2}\).
Tomando la partición \(P=P_1\cup P_2\) que es un refinamiento de \(P_1\) y \(P_2\), se tiene
\[ S(f,P)-s(f,P)\leq S(f,P_1)+S(f,P_2)-s(f,P_1)-s(f,P_2) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon. \]
Por consiguiente \(f\) es integrable Riemann con \(n+1\) discontinuidades, y aplicando el principio de inducción queda probado el resultado.
Teorema 8.7 Si \(f:I\to\mathbb{R}\) es una función integrable en \(I=[a,b]\) y \(g:J\to\mathbb{R}\) es una función continua en \(J=[c,d]\) con \(f(I)\subseteq J\), entonces \(g\circ f\) es integrable en \(I\).
Prueba. Como \(g\) es continua en \(J\), está acotada en \(J\), de manera que podemos tomar \(k>\sup\{g(x):x\in J\}-\inf\{f(x):x\in J\}\).
Por otro lado, como \(J\) es cerrado, \(g\) es uniformemente continua en \(J\) y dado \(\varepsilon>0\), existe \(\delta<\varepsilon\) tal que si \(|x-y|<\delta\) entonces \(|g(x)-g(y)|<\frac{\varepsilon}{2(b-a)}\).
Como \(f\) es integrable en \(I\) podemos tomar una partición \(P=\{x_0,x_1,\ldots,x_n\}\) de \(I\), tal que
\[ S(f,P)-s(f,P) < \frac{\delta^2}{2k}. \]
Para \(i=1,\ldots,n\), sea
\[\begin{align*} m_i &= \inf\{f(x): x\in[x_{i-1},x_i]\}\\ M_i &= \sup\{f(x): x\in[x_{i-1},x_i]\}\\ m_i' &= \inf\{g\circ f(x): x\in[x_{i-1},x_i]\}\\ M_i' &= \sup\{g\circ f(x): x\in[x_{i-1},x_i]\}\\ \end{align*}\]
y sea
\[\begin{align*} A &= \{i\in\{1,\ldots, n\}: M_i-m_i<\delta\}\\ B &= \{i\in\{1,\ldots, n\}: M_i-m_i\geq\delta\} \end{align*}\]
Entonces se cumple que
\[ \delta\sum_{i\in B} (x_i-x_{i-1}) \leq \sum_{i\in B} (M_i-m_i)(x_i-x_{i-1}) \leq \sum_{i=1}^n (M_i-m_i)(x_i-x_{i-1}) < \frac{\delta^2}{2k} \]
de donde se deduce que
\[ \sum_{i\in B} (x_i-x_{i-1}) < \frac{\delta}{2k}. \]
Y utilizando los resultados anteriores se tiene
\[\begin{align*} S(g\circ f,P)-s(g\circ f,P) &= \sum_{i\in A}(M_i'-m_i')(x_i-x_{i-1}) + \sum_{i\in B}(M_i'-m_i')(x_i-x_{i-1}) \\ &< \frac{\varepsilon}{2(b-a)} \sum_{i\in A}(x_i-x_{i-1}) + k \sum_{i\in B}(x_i-x_{i-1})\\ &< \frac{\varepsilon}{2}+\frac{\delta}{2} < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} < \varepsilon, \end{align*}\]
por lo que \(g\circ f\) es integrable en \(I\).
Corolario 8.6 Si \(f:I\to\mathbb{R}\) es una función integrable en \(I=[a,b]\), entonces la función \(|f|\) es integrable en \(I\).
Prueba. Como \(f\) es integrable en \(I\), \(f\) está acotada en \(I\), así que, tomando \(c=\sup\{|f(x)|: x\in I\}\), basta aplicar el teorema anterior con \(g=|x|\) en el intervalo \(J=[-c,c]\).
Corolario 8.7 Si \(f:I\to\mathbb{R}\) es una función integrable en \(I=[a,b]\), entonces la función \(f^n\) es integrable en \(I\) para cualquier \(n\in\mathbb{N}\).
Prueba. Como \(f\) es integrable en \(I\), \(f\) está acotada en \(I\), así que, tomando \(c=\sup\{|f(x)|: x\in I\}\), basta aplicar el teorema anterior con \(g=x^n\) en el intervalo \(J=[-c,c]\).
Corolario 8.8 Si \(f:I\to\mathbb{R}\) es una función integrable en \(I=[a,b]\) tal que \(f(x)>0\) \(\forall x\in I\), entonces la función \(\frac{1}{f}\) es integrable en \(I\).
Prueba. Como \(f\) es integrable en \(I\), \(f\) está acotada en \(I\), así que, tomando \(c=\inf\{f(x): x\in I\}\) y \(d=\sup\{f(x): x\in I\}\), basta aplicar el teorema anterior con \(g=\frac{1}{f}\) en el intervalo \(J=[c,d]\).
Corolario 8.9 Si \(f,g:I\to\mathbb{R}\) son dos funciones integrable en \(I=[a,b]\), entonces la función \(fg\) es integrable en \(I\).
Prueba. Basta tener en cuenta los resultados anteriores y que
\[ fg = \frac{1}{2}((f+g)^2-f^2-g^2) \]
8.5 Teorema fundamental del cálculo
En las secciones anteriores se ha definido la integral de Riemann y hemos estudiado los tipos de funciones integrables, pero, en general, el cálculo de integrales mediante sumas de Riemann suele ser complicado. En esta sección se presenta un importante teorema, al que llegaron Newton y Leibniz de manera simultánea, que relaciona el cálculo integral con el cálculo diferencial y que nos facilitará enormemente el cálculo de integrales sin tener que recurrir a la aproximación mediante sumas de Riemann. Este teorema es tan importante para el Análisis que se ha denominado teorema fundamental del Cálculo.
Definición 8.8 Dada \(f:I\to\mathbb{R}\) integrable en \(I=[a,b]\), se define la integral indefinida de \(f\) en \(I\) como la función
\[ F(x) = \int_a^x f(t)\, dt \]
\(\forall x\in I\).
Antes de enunciar el teorema, presentamos un resultado necesario para su demostración.
Proposición 8.6 Si \(f:I\to\mathbb{R}\) integrable en \(I=[a,b]\), entonces
\[ \left|\int_a^b f(x)\,dx\right| \leq \int_a^b |f(x)|\,dx \]
Prueba. Como \(f\) es integrable en \(I\), por el Corolario 8.6 \(|f|\) también es integrable en \(I\).
Por otro lado, \(-|f|\leq f \leq |f|\), y por las propiedades de la integral se tiene
\[ (-1)\int_a^b |f(x)|\,dx = \int_a^b -|f(x)|\,dx \leq \int_a^b f(x)\,dx \leq \int_a^b |f(x)|\,dx, \]
de donde se deduce que
\[ \left|\int_a^b f(x)\,dx\right| \leq \int_a^b |f(x)|\,dx. \]
Teorema 8.8 Si \(f:I\to\mathbb{R}\) integrable en \(I=[a,b]\) y \(F(x)=\int_a^x f(t)\,dt\) es la integral indefinida de \(f\) en \(I\), entonces \(F\) es continua en \(I\).
Prueba. Como \(f\) es integrable en \(I\), está acotada en \(I\), así que sea \(c=\sup\{|f(x)|: x\in I\}\).
Para cualquier \(\varepsilon>0\) se puede tomar \(\delta =\frac{\varepsilon}{c}>0\), de manera que si \(x,y\in I\) con \(x<y\) y \(|x-y|<\delta\) se tiene, por la proposición anterior,
\[\begin{align*} |F(y)-F(x)| & = \left|\int_a^y f(t)\,dt -\int_a^x f(t)\,dt\right| = \left|\int_x^y f(t)\,dt \right| \\ & \leq \int_x^y |f(t)|\,dt \leq c(y-x) < c\delta = \varepsilon. \end{align*}\]
Luego \(F\) es uniformemente continua en \(I\) y, por tanto, \(F\) es continua en \(I\).
Ejemplo 8.4 Sea
\[ f(x)= \begin{cases} 0 & \mbox{si $x\in [-1,0)$}\\ 1 & \mbox{si $x\in [0,1]$} \end{cases} \]
\(f\) es integrable pues es monótona, y su integral indefinida es
\[ F(x) = \begin{cases} 0 & \mbox{si $x\in [-1,0)$}\\ x & \mbox{si $x\in [0,1]$} \end{cases} \]
ya que para \(0<x<1\) se tiene
\[ F(x) = \int_{-1}^0 f + \int_0^x f = \int_0^x f = \int_0^x 1 = x. \]
Presentamos primero una primera versión del teorema fundamental del cálculo.
Teorema 8.9 (Teorema fundamental del Cálculo I) Dada \(f:I\to\mathbb{R}\) integrable en \(I=[a,b]\) y \(F(x)=\int_a^x f(t)\,dt\) la integral indefinida de \(f\) en \(I\), si \(f\) es continua en \(c\in I\), entonces \(F\) es derivable en \(c\) y \(F'(c)=f(c)\).
Prueba. Dado \(\varepsilon>0\), como \(f\) es continua en \(c\), existe \(\delta>0\) tal que si \(x\in I\) y \(|x-c|<\delta\), entonces \(|f(x)-f(c)|<\varepsilon\).
Tomando \(h\in\mathbb{R}\) con \(|h|<\delta\) y tal que \(c+h\in I\), se tiene
\[\begin{align*} \left|\frac{F(c+h)-F(c)}{h}-f(c)\right| & = \left|\frac{\int_a^{c+h}f(t)\,dt -\int_a^c f(t)\,dt}{h} -f(c)\right| \\ & = \left|\left(\frac{1}{h}\int_c^{c+h}f(t)\,dt\right)-f(c)\right| \\ & = \left|\frac{1}{h}\left(\int_c^{c+h}f(t)\,dt - hf(c)\right)\right| \\ & = \left|\frac{1}{h}\left(\int_c^{c+h}f(t)\,dt - \int_c^{c+h} f(c)\,dt\right)\right|\\ & = \left|\frac{1}{h}\int_c^{c+h}(f(t)-f(c))\,dt\right| \\ & = \frac{1}{|h|} \left|\int_c^{c+h}(f(t)-f(c))\,dt\right|\\ & \leq \frac{1}{|h|} \varepsilon |h| = \varepsilon. \end{align*}\]
Por tanto, \(F'(c) = \lim_{h\to 0} \frac{F(c+h)-F(c)}{h} = f(c)\).
La importancia de este teorema radica en que conecta el concepto de derivada, al cuál se llegó mediante el estudio de las tangentes a la gráfica de una función, y el concepto de integral, al cuál hemos llegado mediante el estudio del área encerrada entre la gráfica de la función y el eje \(x\).
Este teorema nos garantiza que si \(f\) es continua en en el punto \(c\), la integral indefinida \(F\) es derivable en ese punto y su derivada coincide con \(f(c)\), pero no nos permite calcular la integral definida, ya que, como veremos a continuación, existen infinitas funciones con derivada \(f(c)\).
Definición 8.9 (Primitiva de una función) Dada una función \(f:I\to\ \mathbb{R}\) integrable en \(I\), a cualquier función \(F\) que cumple \(F'=f\) se le llama primitiva de \(f\).
Si \(F\) es una primitiva de \(f\), entonces \(f\) tiene infinitas primitivas, ya que \((F+C)' = F'+C' = F'+0 = F' = f\), y por tanto, \((F+C)\) también es una primitiva de \(f\) \(\forall C\in\mathbb{R}\).
Ejemplo 8.5 Dada la función \(f(x)=2x\), es fácil ver que \(F(x)=x^2+C\) es una primitiva de \(f\) para cualquier \(C\in\mathbb{R}\).
En el Ejemplo 13.1 vimos que \(\int_0^1 x\,dx = \frac{1}{2}\), de modo que \[ \int_0^1 2x\,dx = 2 \int_0^1 x\,dx = 2\frac{1}{2} = 1. \]
Si queremos llegar a este resultado usando primitivas, es necesario tomar la primitiva adecuada, es decir, necesitamos saber el valor concreto de la constante \(C\) que permite calcular la integral definida. En este caso particular, como \(F\) tiene que cumplir que \(F(1)=1+C = 1=\int_0^1 2x\,dx\), resulta evidente que debe ser \(C=0\), pero si tomamos cualquier otra constante, como por ejemplo \(C=1\), entonces \(F(1) = 1+1 = 2\neq 1 = \int_0^1 2x\,dx\).
Afortunadamente, la segunda parte del teorema fundamental del cálculo resuelve este inconveniente.
Teorema 8.10 (Teorema fundamental del cálculo II) Si \(f:I\to\mathbb{R}\) es integrable en \(I=[a,b]\) y \(F\) es una primitiva de \(f\) en \(I\), entonces
\[ \int_a^b f(x)\,dx = F(b)-F(a). \]
Prueba. Dado \(\varepsilon>0\), sea \(P=\{x_0,x_1,\ldots,x_n\}\) una partición de \(I\) tal que \(S(f,P)-s(f,P)<\varepsilon\).
Como \(F\) es continua en \(I\), por el Teorema 7.6, para \(i=1,\ldots,n\), existe \(t_i \in (x_i,x_{i+1})\) tal que
\[ F(x_i)-F(x_{i-1}) = F'(t_i)(x_i-x_{i-1}) = f(t_i)(x_i-x_{i-1}). \]
Entonces,
\[ \sum_{i=1}^n f(t_i)(x_i-x_{i-1}) = \sum_{i=1}^n (F(x_i)-F(x_{i-1})) = F(b)-F(a). \]
Pero,
\[ s(f,P)\leq \sum_{i=1}^n f(t_i)(x_i-x_{i-1}) \leq S(f,P), \]
por lo que
\[ \left|F(b)-F(a)-\int_a^b f(x)\,dx\right|<\varepsilon, \]
y por tanto,
\[ \int_a^b f(x)\,dx = F(b)-F(a). \]
Este teorema, que también se conoce como al regla de Barrow, nos permitirá calcular la integral definida de una función a partir de cualquier primitiva suya, sin necesidad de usar las sumas de Riemann.
Ejemplo 8.6 Dada la función \(f(x)=x^2\), la función \(F_0(x)= \frac{x^3}{3}\) es una primitiva de \(f\), y por tanto, podemos usarla para calcular la siguiente integral
\[ \int_0^1 x^2\, dx = F_0(1)-F_0(0) = \frac{1^3}{3}-\frac{0^3}{3} = \frac{1}{3}. \]
Pero podríamos haber utilizado cualquier primitiva de \(f\), como por ejemplo \(F_1(x) = \frac{x^3}{3}+1\), ya que
\[ \int_0^1 x^2\, dx = F_1(1)-F_1(0) = \frac{1^3}{3}+1-\left(\frac{0^3}{3}+1\right) = \frac{1}{3}+1-1 = \frac{1}{3}. \]
Ejemplo 8.7 Dada la función \(f(x)=\cos(x)\), la función \(F(x)= \operatorname{sen}(x)\) es una primitiva de \(f\), y por tanto, podemos usarla para calcular la siguiente integral
\[ \int_{\pi/2}^\pi \cos(x)\, dx = F(\pi)-F(\pi/2) = \operatorname{sen}(\pi)-\operatorname{sen}(\pi/2) = 0-1 = -1. \]
Hemos visto que si \(f\) es continua en un intervalo \(I=[a,b]\), entonces \(f\) tiene primitiva en \(I\), pero no toda función integrable en \(I\) tiene primitiva.
Ejemplo 8.8 La función
\[ f(x) = \begin{cases} 1 & \mbox{si $x=1/2$}\\ 0 & \mbox{si $x\in [0,1]\setminus\{1/2\}$} \end{cases} \]
es integrable en el intervalo \([0,1]\), y \(\int_0^1 f(x)\,dx = 0\), sin embargo, \(f\) no es continua en \([0,1]\) y no verifica el teorema de los valores intermedios, ya que para cualquier \(y\in(0,1/2)\), no existe \(x\in[0,1/2]\) tal que \(f(x)=y\). Por tanto, según el teorema de Darboux (Teorema 7.9), \(f\) no es la derivada de ninguna función en \([0,1]\), por lo que no tiene primitiva.
También puede darse el caso de que \(f\) tenga primitiva, y sin embargo, no sea integrable.
Ejemplo 8.9 La función
\[ f(x)= \begin{cases} x^2\operatorname{sen}\left(\frac{1}{x^2}\right) & \mbox{si $x\in[-1,1]\setminus\{0\}$}\\ 0 & \mbox{si $x=0$} \end{cases} \]
es derivable en cualquier punto de \([-1,1]\) y \(f'(x) = 2x\operatorname{sen}\left(\frac{1}{x^2}\right)-\frac{2\cos\left(\frac{1}{^2}\right)}{x}\), que no está acotada en \([-1,1]\), y por tanto no es integrable en \([-1,1]\).
8.6 Cálculo de areas
Tal y como se ha definido la integral de una función a partir de las sumas de Riemann, no resulta extraño que la principal aplicación de las integrales definidas sea el cálculo del areas encerrada por la gráfica de una función y el eje \(x\) en un intervalo de \(I\). Ya hemos visto que cuando \(f(x)\geq 0\) \(\forall x\in I\), si \(f\) es integrable en \(I=[a,b]\), entonces \(\int_a^b f(x)\, dx\geq 0\) es el área encerrada entre la gráfica de la función \(f\) y el eje \(x\) en el intervalo \(I\). En esta sección veremos cómo calcular áreas de funciones que también presentan valores negativos en el intervalo de integración y generalizamos el resultado para calcular áreas encerradas entre las gráficas de dos funciones.
8.6.1 Cálculo del area encerrada por una función y el eje \(x\).
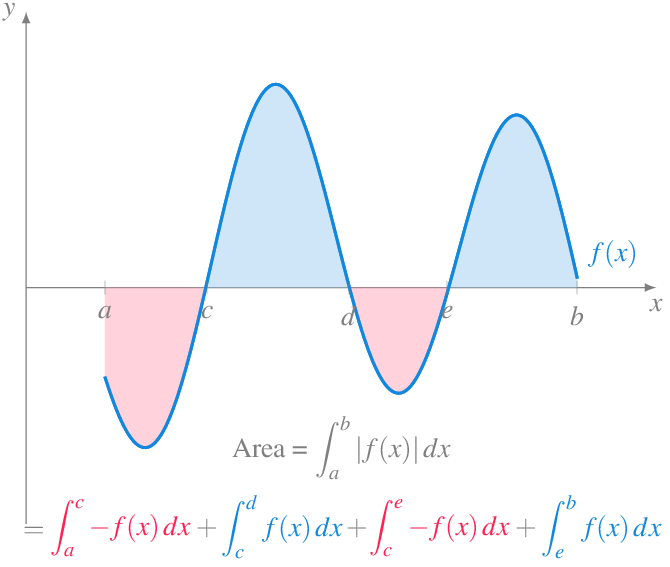
Ya hemos visto que cuando una función \(f(x)<0\) \(\forall x\in I=[a,b]\), entonces \(\int_a^b f(x)\, dx<0\), de manera que no puede interpretarse como un área porque geométricamente no tienen sentido las áreas negativas. En general, para evitar este problema, si queremos calcular el área encerrada por la gráfica de una función \(f(x)\) en un intervalo \(I=[a,b]\) debemos calcular la integral definida en \(I\) del valor absoluto de la función, es decir,
\[ \int_a^b |f(x)|\,dx. \]
Ahora bien, para calcular esta integral mediante primitivas, haciendo uso del teorema fundamental del cálculo, normalmente se recurre a descomponer el intervalo de integración en subintervalos donde la función sea positiva o negativa, integrar \(f\) en los intervalos donde la función es positiva, integrar \(-f\) en los intervalos donde la función es negativa, y finalmente, sumar las areas correspondientes a cada subintervalo.
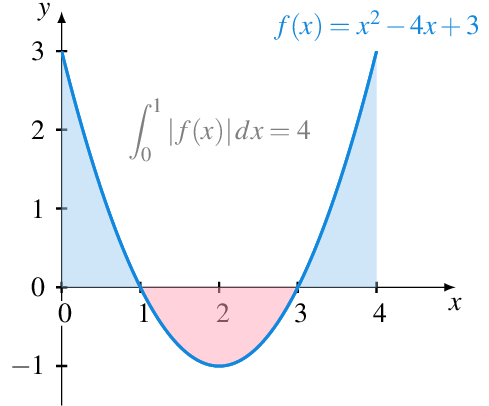
Ejemplo 8.10 Veamos cómo calcular el area encerrada entre la gráfica de la función \(f(x)=x^2-4x+3\) y el eje \(x\) en el intervalo \([0,4]\).
Si resolvemos la ecuación \(f(x)=0\) obtenemos dos raíces \(x=1\) y \(x=3\), de manera que la función es positiva en el intervalo \((0,1)\) y \((3,4)\) y negativa en el intervalo \((1,3)\). Por tanto, el área encerrada entre la gráfica de la función y el eje \(x\) es
\[\begin{align*} \int_0^4 |f(x)|\,dx &= \int_0^1 x^2-4x+3\,dx -\int_1^3 x^2-4x+3\,dx + \int_3^4 x^2+4x+3\,dx\\ &= \left[\frac{x^3}{3}-2x^2+3x\right]_0^1 + \left[\frac{x^3}{3}-2x^2+3x\right]_1^3 + \left[\frac{x^3}{3}-2x^2+3x\right]_3^4 \\ &= \frac{4}{3} - \frac{-4}{3} + \frac{4}{3} = 4 \end{align*}\]
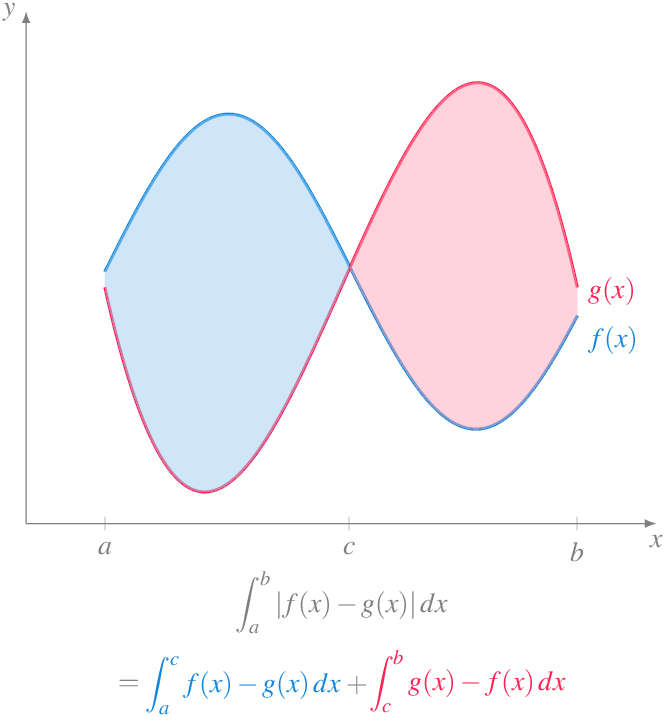
8.6.2 Area encerrada entre dos funciones
Si en lugar de calcular el área encerrada entre la gráfica de una función \(f\) y el eje \(x\) en un intervalo \(I=[a,b]\), se quiere calcular el area encerrada entre dos funciones \(f\) y \(g\) en un intervalo \(I=[a,b]\), basta con integrar la diferencia entre las dos funciones \(f-g\). Pero como \(f\) puede ser mayor que \(g\) en algún subintervalo de \(I\) y menor en otros, para asegurarnos de calcular el area correcta, hay que integrar el valor absoluto de la diferencia, es decir,
\[ \int_a^b |f(x)-g(x)|\, dx \]
Al igual que antes, para calcular esta integral mediante primitivas, haciendo uso del teorema fundamental del cálculo, tendremos que descomponer el intervalo de integración en subintervalos donde la diferencia \(f-g\) sea sea positiva o negativa, integrar \(f-g\) en los intervalos donde la diferencia es positiva, integrar \(-(f-g)=g-f\) en los intervalos donde la diferencia es negativa, y finalmente, sumar las areas correspondientes a cada subintervalo.
Ejemplo 8.11 Veamos cómo calcular el area encerrada entre las gráficas de las funciones \(f(x)=\operatorname{sen}(x)\) y \(g(x)=\cos(x)\) en el intervalo \([0,\pi]\).
Si resolvemos la ecuación \(f(x)-g(x)=0\) obtenemos una raíz en \(x=\pi/4\) en el intervalo de integración. Se cumple que \(f(x)<g(x)\) \(\forall x\in\left(0,\frac{\pi}{4}\right)\) y \(f(x)>g(x)\) \(\forall x\in\left(\frac{\pi}{4},\pi\right)\). Por tanto, el área comprendida entre las gráficas de \(f\) y \(g\) en el intervalo \([0,\pi]\) es
\[\begin{align*} \int_0^\pi |f(x)-g(x)|\,dx &= \int_0^{\pi/4} \cos(x)-\operatorname{sen}(x)\,dx +\int_{\pi/4}^{\pi} \operatorname{sen}(x)-\cos(x)\,dx\\ &= \left[\operatorname{sen}(x)+\cos(x)\right]_0^{\pi/4} + \left[-\cos(x)-\operatorname{sen}(x)\right]_{\pi/4}^{\pi} \\ &= \sqrt{2}-1 +\sqrt{2}+1 = 2\sqrt{2} \end{align*}\]
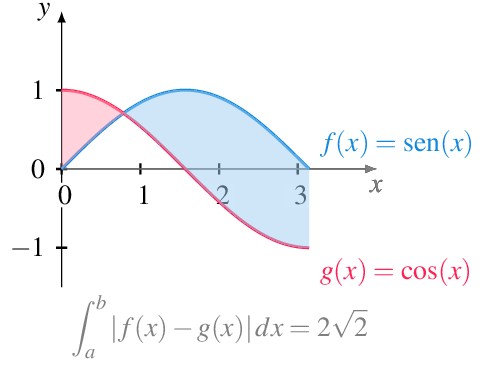
8.6.3 Cálculo del area encerrada por una curva en coordenadas polares
En ocasiones, para calcular el area encerrada por una curva, especialmente para curvas dadas mediante una ecuación implícita, resulta más sencillo trabajar en coordenadas polares.
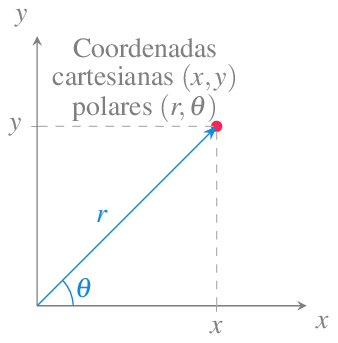
Para pasar de coordenadas cartesianas a coordenadas polares, primero se obtiene el valor de \(r\) aplicando el teorema de Pitágoras
\[ r = \sqrt{x^2+y^2} \]
y después se obtiene el ángulo aplicando relaciones trigonométricas
\[ \theta = \begin{cases} \operatorname{arccos}\left(\frac{x}{r}\right) & \mbox{si $y\geq 0$}\\ -\operatorname{arccos}\left(\frac{x}{r}\right) & \mbox{si $y<0$} \end{cases} \]
suponiendo \(r\neq 0\).
Y para pasar de coordenadas polares a coordenadas cartesianas se aplican las siguientes relaciones trigonométricas
\[\begin{align*} x &= r \cos(\theta)\\ y &= r \operatorname{sen}(\theta) \end{align*}\]
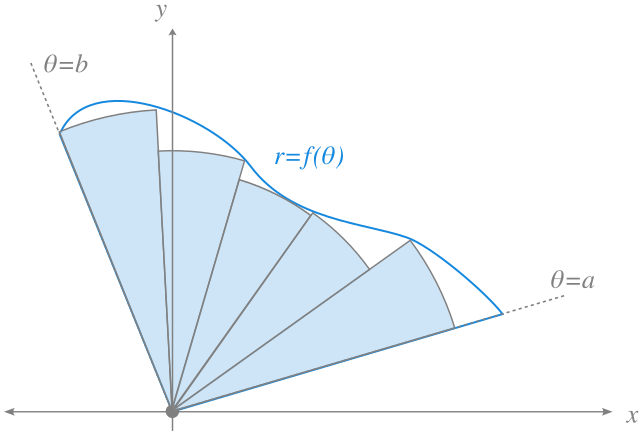
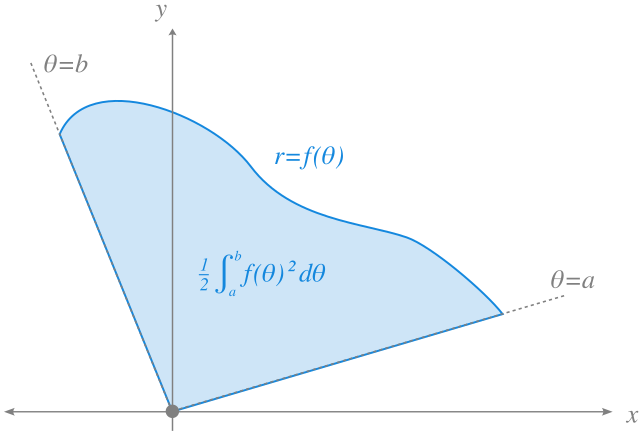
Para calcular el area encerrada por una curva dada en coordenadas polares \(r=f(\theta)\) y las rectas \(\theta=a\) y \(\theta=b\), se puede utilizar una aproximación similar a las sumas de Riemann, descomponiendo el area en sectores de círculo con ángulos en una partición \(P=\{\theta_0=a, \theta_1, \ldots, \theta_n=b\}\) de \(I=[a,b]\). Si para cada uno de estos sectores se toma como radio el ínfimo de \(f(\theta)\) en el correspondiente subintervalo, surgen las sumas inferiores
\[ s(f,P) = \sum_{i=1}^n \pi m_i^2\frac{(\theta_i-\theta_{i-1})}{2\pi} = \sum_{i=1}^n \frac{m_i^2}{2}(\theta_i-\theta_{i-1}) \]
donde \(m_i=\inf\{f(\theta): \theta\in[\theta_{i-1},\theta_i]\}\) para \(i=1,\ldots,n\).
Mientras que si para cada uno de estos sectores se toma como radio el supremo de \(f(\theta)\) en el correspondiente subintervalo, surgen las sumas superiores
\[ S(f,P) = \sum_{i=1}^n \pi M_i^2\frac{(\theta_i-\theta_{i-1})}{2\pi} = \sum_{i=1}^n \frac{M_i^2}{2}(\theta_i-\theta_{i-1}) \]
donde \(M_i=\sup\{f(\theta): \theta\in[\theta_{i-1},\theta_i]\}\) para \(i=1,\ldots,n\).
De forma análoga se puede definir integral inferior de \(f\) en \(I\) como \(\underline{\int_a^b} f =\sup\{s(f,P): P\in \mathcal{P}(I)\}\) y la integral superior de \(f\) en \(I\) como el número \(\overline{\int_a^b} f =\inf\{S(f,P): P\in \mathcal{P}(I)\}\), de manera que, si la integral inferior coincide con la superior, la función es integrable y
\[ \int_a^b \frac{f(\theta)^2}{2}\,d\theta \]
mide el área encerrada por la curva \(r=f(\theta)\) y las rectas \(\theta=a\) y \(\theta=b\).
Ejemplo 8.12 Un semicírculo de radio \(r\) puede expresarse en coordenadas polares mediante la función \(f(\theta)=r\) para \(0\leq \theta\leq \pi\). Por tanto, el área encerrada por este semicírculo es
\[ \int_0^{\pi} \frac{r^2}{2} \,d\theta = \left[\frac{r^2}{2}\theta\right]_0^\pi = \frac{r^2}{2}\pi. \]
Ejemplo 8.13 Veamos ahora cómo calcular el area encerrada por la curva polar \(r=3\operatorname{sen}(2\theta)\).
\[\begin{align*} \int_0^{2\pi} \frac{r^2}{2} &= \frac{1}{2}\int_0^{2\pi} (3\operatorname{sen}(2\theta))^2\,d\theta = \frac{9}{2}\int_0^{2\pi} \operatorname{sen}(2\theta)^2\,d\theta \\ &= \frac{9}{2}\int_0^{2\pi} \frac{1 - \cos(4\theta)}{2}\,d\theta = \frac{9}{4}\left[\theta - \frac{\operatorname{sen}(4\theta)}{4}\right]_0^{2\pi} \\ &= \frac{9}{4}\left(2\pi - \frac{\operatorname{sen}(8\pi)}{4}\right) = \frac{9}{4}2\pi = \frac{9}{2}\pi. \end{align*}\]
8.6.4 Cálculo del area encerrada por dos curvas en coordenadas polares
También es posible calcular el area encerrada por dos curvas en coordenadas polares de forma análoga a como se hizo para el area encerrada entre dos funciones en coordenadas cartesianas.
Si tenemos dos curvas polares \(r=f(\theta)\) y \(r=g(\theta)\), con \(f(\theta)\leq g(\theta)\) \(\forall \theta\in[a,b]\), el area encerrada entre estas dos curvas en el intervalo \([a,b]\) puede calcularse restando el area encerrada por \(g\) al area encerrada por \(f\), es decir,
\[ \frac{1}{2} \int_a^b f(\theta)^2\,d\theta - \frac{1}{2} \int_a^b g(\theta)^2\,d\theta = \frac{1}{2} \int_a^b f(\theta)^2-g(\theta)^2\,d\theta \]
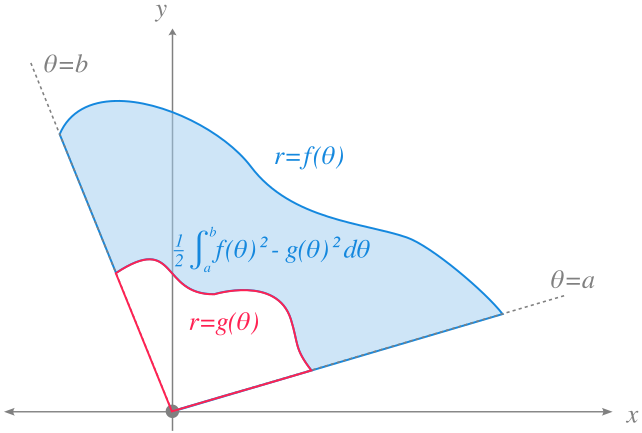
En general, cuando \(f\) es mayor que \(g\) en algunos subintervalos de \(I\) y menor en otros, habrá que descomponer el intervalo de integración en subintervalos donde la diferencia \(f-g\) sea sea positiva o negativa, integrar \(f-g\) en los intervalos donde la diferencia es positiva, integrar \(-(f-g)=g-f\) en los intervalos donde la diferencia es negativa, y finalmente, sumar las areas correspondientes a cada subintervalo.
Ejemplo 8.14 Vamos a calcular el area encerrada entre las curvas polares \(f(\theta)=3\cos(\theta)\) y \(g(\theta)=1+\cos(\theta)\). Para ello primero debemos determinar el intervalo de integración a partir de los puntos de corte de las dos curvas.
\[ 3\cos(\theta) = 1 + \cos(\theta) \Leftrightarrow \cos(\theta) = \frac{1}{2} \Leftrightarrow \theta = \operatorname{arccos}\left(\frac{1}{2}\right) = \pm \frac{\pi}{3} \]
Así pues, el intervalo de integración es \([-\frac{\pi}{3},\frac{\pi}{3}]\). Como en este intervalo \(1+\cos(\theta) \leq 3\cos(\theta)\), el area encerrada entre estas dos curvas es
\[\begin{align*} \frac{1}{2}\int_{-\pi/3}^{\pi/3}f(\theta)^2-g(\theta)^2\,d\theta &= \frac{1}{2} \int_{-\pi/3}^{\pi/3}(3\cos(\theta))^2 - (1+\cos(\theta))^2 \,d\theta \\ &= \frac{1}{2} \int_{-\pi/3}^{\pi/3}8\cos(\theta)^2 - 2\cos(\theta) - 1 \,d\theta \\ &= \frac{1}{2}8\left(\int_{-\pi/3}^{\pi/3}\cos(\theta)^2\,d\theta - 2\int_{-\pi/3}^{\pi/3}\cos(\theta)\,d\theta - \int_{-\pi/3}^{\pi/3}\,d\theta \right) \\ &= \frac{1}{2}\left([2\operatorname{sen}(2\theta)+4\theta]_{-\pi/3}^{\pi/3} - 2[\operatorname{sen}(\theta)]_{-\pi/3}^{\pi/3} - [\theta]_{-\pi/3}^{\pi/3} \right) \\ &= \frac{1}{2}\left(\sqrt{3}+\frac{4\pi}{3} +\sqrt{3} -\frac{4\pi}{3}- \sqrt{3} - \sqrt{3} - \frac{\pi}{3} -\frac{\pi}{3}\right)\\ &= \pi. \end{align*}\]
8.7 Integrales impropias
El concepto de integral definida de una función en un intervalo cerrado \([a,b\)] y se puede generalizar a intervalos no acotados y también a funciones con discontinuidades de salto infinito.
Definición 8.10 (Integral impropia de primer tipo) Dada una función \(f:I\to\mathbb{R}\) integrable en \(I=[a,t]\) para \(\forall t>a\), se define la integral impropia de \(f\) en el intervalo \([a,\infty)\) como el límite
\[ \int_a^\infty f(x)\,dx = \lim_{t\to\infty} \int_a^t f(x)\,dx \]
siempre que este límite exista, en cuyo caso se dice que la integral impropia converge.
Del mismo modo, si \(f\) es integrable en \(I=[t,a]\) para \(\forall t<a\), se define la integral impropia de \(f\) en el intervalo \((-\infty, a]\) como el límite
\[ \int_{-\infty}^a f(x)\,dx = \lim_{t\to\infty} \int_t^a f(x)\,dx. \]
Finalmente, si \(\int_{-\infty}^a f(x)\,dx\) y \(\int_a^\infty f(x)\,dx\) convergen, se define la integral impropia de \(f\) en el intervalo \((-\infty, \infty)\) como
\[ \int_{-\infty}^\infty f(x)\,dx = \int_{-\infty}^a f(x)\,dx + \int_a^\infty f(x)\,dx \]
Para funciones positivas en los dominios de integración, estas integrales impropias pueden interpretarse también como áreas. En particular, \(\int_a^\infty f(x)\,dx\) es el area encerrada por la gráfica de \(f\) y el eje \(x\) en el intervalo \([a,\infty)\), \(\int_{-\infty}^\infty f(x)\,dx\) es el area encerrada por la gráfica de \(f\) y el eje \(x\) en el intervalo \((-\infty,a]\) y \(\int_{-\infty}^\infty f(x)\,dx\) es el area encerrada por la gráfica de \(f\) y el eje \(x\) en todo \(\mathbb{R}\).
Ejemplo 8.15 La integral impropia de la función \(f(x)=\frac{1}{x^2}\) converge en el intervalo \([1,\infty]\) ya que
\[ \int_1^\infty \frac{1}{x^2}\,dx = \lim_{t\to\infty} \int_1^t \frac{1}{x^2}\,dx = \lim_{t\to\infty}\left[\frac{-1}{x}\right]_1^t = \lim_{n\to\infty} 1-\frac{1}{t} = 1. \]
Por tanto, el área que queda encerrada por la gráfica de \(f\) y el eje \(x\) por encima de \(1\) es finita y vale \(1\).
Sin embargo, la integral impropia de la función \(g(x)=\frac{1}{x}\) diverge en el intervalo \([1,\infty]\) ya que
\[ \int_1^\infty \frac{1}{x}\,dx = \lim_{t\to\infty} \int_1^t \frac{1}{x}\,dx = \lim_{t\to\infty}\left[\ln(x)\right]_1^t = \lim_{n\to\infty} \ln(t) = \infty. \]
Y por tanto, el área que queda encerrada por la gráfica de \(g\) y el eje \(x\) por encima de \(1\) es infinita.
En estos casos la región encerrada por la gráfica de la función y el eje \(x\) se extiende de manera infinita a lo largo del eje \(x\). La misma idea puede aplicarse para calcular areas de regiones encerradas por la gráfica de \(f\) y el eje \(y\) cuando estas regiones se extienden de manera infinita porque la función no está acotada en algún valor del dominio de integración.
Definición 8.11 (Integral impropia de segundo tipo) Dada una función \(f:I\to\mathbb{R}\) continua en \(I=[a,b)\) y discontinua en \(b\), se define la integral impropia de \(f\) en \(I\) como el límite
\[ \int_a^b f(x)\,dx = \lim_{t\to b^-} \int_a^t f(x)\,dx \]
siempre que este límite exista, en cuyo caso se dice que la integral impropia converge.
8.8 Cálculo de volúmenes
Otra de las aplicaciones habituales de las integrales es el cálculo de volúmenes de cuerpos sólidos tridimensionales con secciones transversales regulares. El procedimiento es similar al utilizado para el cálculo de areas de regiones planas, pero en lugar de aproximar el area mediante sumas de Riemann de rectángulos, se utilizan sumas de Riemann de figuras geométricas de volumen conocido, habitualmente discos o envoltorios cilíndricos. Para ello tomaremos secciones transversales del cuerpo sólido del que se quiere calcular el volumen con respecto a alguno de los ejes a lo largo de una partición del intervalo donde está definido el sólido en ese eje.
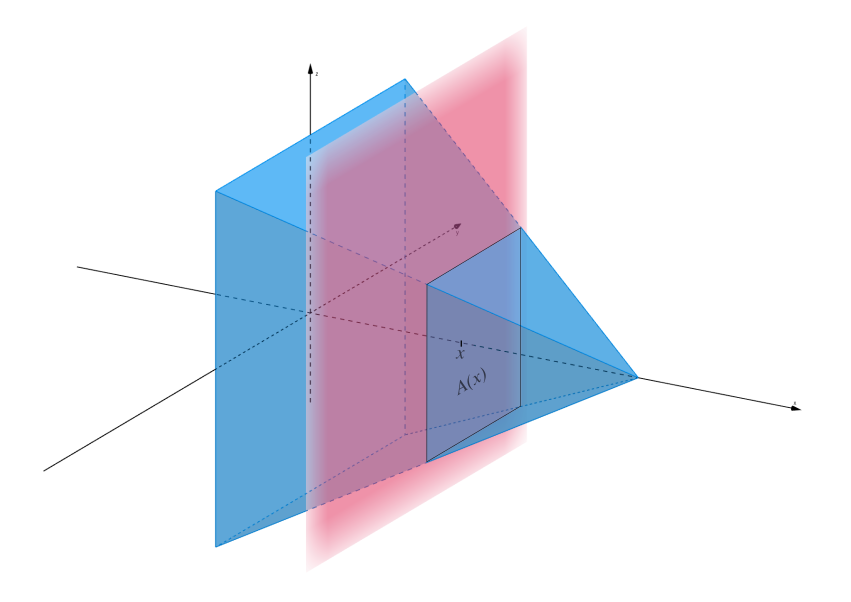
En general, si disponemos de una función \(A(x)\) que nos da el área de la sección transversal del sólido para cada \(x\in[a,b]\), podemos tomar una partición \(P_n=\{x_0=a,x_1,\ldots, x_n=b\}\) del intervalo \([a,b]\) y aproximar el volumen del sólido en este intervalo mediante las sumas inferior y superior de Riemann
\[\begin{align*} s(A,P_n) &= \sum_{i=1}^n m_i(x_i-x_{i-1}),\quad m_i=\inf\{A(x): x\in(x_{i-1},x_i)\}\\ S(A,P_n) &= \sum_{i=1}^n M_i(x_i-x_{i-1}),\quad M_i=\sup\{A(x): x\in(x_{i-1},x_i)\} \end{align*}\]
donde \(m_i (x_i-x_{i-1})\) es el volumen de un disco cilíndrico de base \(m_i\) y altura \(x_i-x_{i-1}\), y \(M_i (x_i-x_{i-1})\) es el volumen de un cilindro de base \(M_i\) y altura \(x_i-x_{i-1}\).
Calculadora de volúmenes de sólidos de revolución mediante discos cilíndricos.
Como ya hemos visto, si \(\lim_{n\to\infty} s(A,P_n) = \lim_{n\to\infty} S(A,P_n)\), la función \(A(x)\) es integrable Riemann en el intervalo \([a,b]\) y
\[ \int_a^b A(x)\,dx = \lim_{n\to\infty} s(A,P_n) = \lim_{n\to\infty} S(A,P_n), \]
mide el volumen del cuerpo sólido con secciones transversales de área \(A(x)\) en el intervalo \([a,b]\).
Ejemplo 8.16 Veamos cómo calcular el volumen de una esfera de radio \(r\) centrada en el origen con ecuación \(x^2+y^2+z^2=r^2\). Si cortamos la esfera con planos \(x=x_i\) perpendiculares al eje \(x\), sustituyendo en la ecuación de la esfera, se tiene \(y^2+z^2=r^2-x_i^2\), por lo que se obtienen secciones transversales circulares con radio \(\sqrt{r^2-x_i^2}\), y, por tanto, el área de estas secciones circulares será \(\pi \left(\sqrt{r^2-x_i^2}\right)^2= \pi (r^2-x_i^2)\). Así pues, la función que nos da el área de la sección transversal para cualquier \(x\in[-r,r]\) es \(A(x)=\pi(r^2-x^2)\), y por tanto, podemos calcular el volumen de la esfera con la integral definida
\[\begin{align*} \int_{-r}^r \pi(r^2-x^2)\,dx &= \pi\left[r^2x-\frac{x^3}{3}\right]_{-r}^r \\ &= \pi\left(r^2r-\frac{r^3}{3}-\left(r^2(-r)-\frac{(-r)^3}{3}\right)\right) \\ &= 2r^3 - \frac{2r^3}{3} = \frac{4}{3}\pi r^3. \end{align*}\]
8.8.1 Cálculo de volúmenes de sólidos de revolución con discos cilíndricos
Cuando el sólido se obtiene rotando una función \(f(x)\) alrededor del eje \(x\), se dice que el sólido resultante es un sólido de revolución.
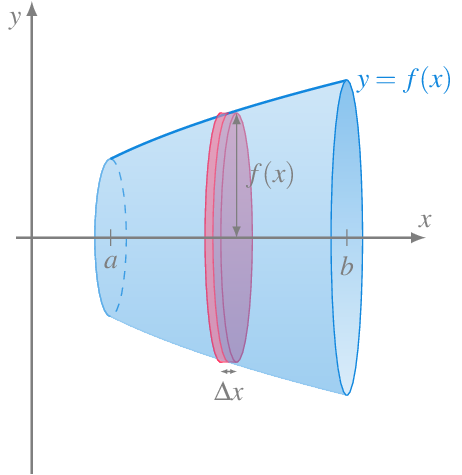
Este tipo de sólidos tiene la particularidad de que todas sus secciones transversales con respecto al eje de rotación son círculos de radio \(f(x)\), por lo que el área de las secciones transversales es \(A(x)=\pi f(x)^2\), y su volumen en el intervalo \([a,b]\) puede calcularse mediante la integral definida
\[ \int_a^b \pi f(x)^2\,dx \]
Ejemplo 8.17 Si rotamos alrededor del eje \(x\) el segmento de la recta \(f(x)=2-x\) correspondiente al intervalo \(x\in[0,2]\), se obtiene un cono con base de radio \(2\) y altura \(2\). El volumen de este cono es
\[\begin{align*} \int_0^2 \pi f(x)^2\,dx &= \int_0^2 \pi (2-x)^2\,dx = \pi \int_0^2 x^2-4x+4\,dx \\ &= \pi \left[\frac{x^3}{3}-2x^2+4x\right]_0^2 = \pi\left(\frac{2^3}{3}-2\cdot 2^2+4\cdot 2\right) = \frac{8}{3}\pi. \end{align*}\]
8.8.2 Cálculo de volúmenes de sólidos de revolución con envoltorios cilíndricos
Otra forma de calcular volúmenes de sólidos de revolución es mediante envoltorios o envolventes cilíndricas como los de figura de mas abajo.
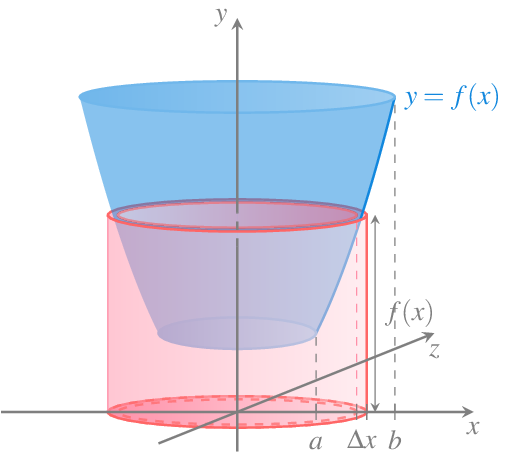
Los envoltorios se construyen de forma que su base es un círculo de radio \(x\in [a,b]\) y perpendicular al eje de rotación del sólido de revolución y su altura es \(f(x)\), de manera que su área (sin contar el área de las bases) es \(2\pi x f(x)\). Sumando las áreas de estos infinitos envoltorios que se obtienen para cada \(x\in[a,b]\) se obtiene al volumen del cuerpo sólido de revolución en el intervalo \([a,b]\) mediante la integral definida
\[ \int_a^b 2\pi x f(x)\,dx \]
Calculadora de volúmenes de sólidos de revolución mediante envoltorios cilíndricos.
Ejemplo 8.18 El volumen del sólido de revolución que se obtiene al rotar alrededor del eje \(y\) la función \(f(x)=4-x^2\) en el intervalo \([0,2]\) puede calcularse usando tanto discos como envoltorios cilíndricos.
Si usamos discos discos cilíndricos debemos expresar \(x\) en función de \(y\), es decir \(x=\sqrt{4-y}\) y calcular la siguiente integral definida en el intervalo \([0,4]\)
\[ \int_0^4 \pi g(y)^2\,dy = \int_0^4 \pi \left(\sqrt{4-y}\right)^2\,dy = \pi\left[4y-\frac{y^2}{2}\right]_0^4 = \pi\left(16-\frac{4^2}{2}\right) = 8\pi. \]
Mientras que si usamos envoltorios cilíndricos hay que calcular la integral
\[ \int_0^2 2\pi x f(x)\,dx = \int_0^2 2\pi x\cdot (4-x^2)\,dx = 2\pi\left[2x^2-\frac{x^4}{4}\right]_0^2 = 2\pi \left(8-\frac{2^4}{4}\right) = 8\pi. \]
8.9 Cálculo de la longitud de una curva
Otra importante aplicación geométrica de las integrales es el cálculo de la longitud de una curva dada por una función en un intervalo \([a,b]\). Una vez más, la idea consiste en dividir el intervalo \([a,b]\) en \(n\) subinvervalos de igual amplitud mediante una partición \(P_n=\{x_0=a, x_1, \ldots, x_n=b\}\) con \(\Delta x = x_i-x{i-1}\) \(i=1,\ldots,n\), y para cada subintervalo \([x_{i-1}, x_i]\) tomar el segmento que une los puntos \((x_{i-1}, f(x_{i-1}))\) y \((x_i,f(x_i))\). La suma de todos los segmentos correspondientes a la partición tomada nos dará una aproximación de la longitud de la curva de la función en el intervalo \([a,b]\).
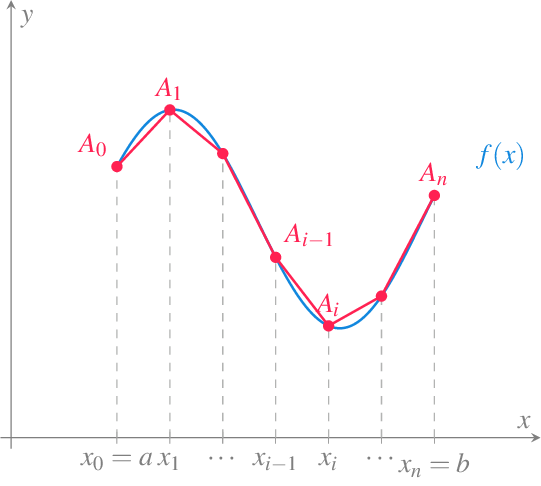
Aplicando el teorema de Pitágoras, es fácil ver que la longitud del segmento correspondiente al subintervalo \([x_{i-1},x_i]\) es
\[ \sqrt{(x_i-x_{i-1})^2+(f(x_i)-f(x_{i-1}))^2} = \sqrt{\Delta x^2+(f(x_i)-f(x_{i-1}))^2}. \]
Por otro lado, si \(f\) es diferenciable en \([x_{i-1},x_{i}]\), según el teorema del valor medio, se tiene que existe un \(x'_i\in [x_{i-1},x_i]\) tal que
\[ f'(x'_i) = \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \]
de manera que
\[ f(x_i)-f(x_{i-1})=f'(x'_i)(x_i-x_{i-1}) = f'(x'_i)\Delta x, \]
y la longitud del segmento puede expresarse como
\[\begin{align*} \sqrt{\Delta x^2+(f(x_i)-f(x_{i-1}))^2} &= \sqrt{\Delta x^2+(f'(x'_i)\Delta x^2}\\ &= \Delta x\sqrt{1+f'(x'_i)^2}, \end{align*}\]
y la suma de todos los segmentos resulta
\[ \sum_{i=1}^n \sqrt{1+f'(x'_i)^2}\Delta x \]
Resulta evidente, que a medida que aumentemos el número de subintervalos \(n\) de la partición, la aproximación de la longitud de la curva será mejor y en el límite tendremos su valor exacto, que puede calcularse mediante la integral definida
\[ \lim_{n\to\infty} \sum_{i=1}^n \sqrt{1+f'(x'_i)^2} \Delta x = \int_a^b \sqrt{1+f'(x)^2}\, dx, \]
siempre y cuando \(f'(x)\) sea integrable en \([a,b]\).
Ejemplo 8.19 Veamos cómo calcular la longitud de una circunferencia de radio \(1\) centrada en el origen con ecuación \(x^2+y^2=1\). Resolviendo esta ecuación para \(y\) se tiene que \(y=\pm \sqrt{1-x^2}\), y podemos tomar la función \(f(x)=\sqrt{1-x^2}\) cuya gráfica es la semicircunferencia superior.
La derivada de \(f\) es \(f'(x)=\frac{-x}{\sqrt{1-x^2}}\), de manera que la longitud de la semicircunferencia es
\[\begin{align*} \int_{-1}^1 \sqrt{1+\left(\frac{-x}{\sqrt{1-x^2}}\right)^2}\,dx &= \int_{-1}^1 \sqrt{1+\frac{x^2}{1-x^2}}\,dx = \int_{-1}^1 \sqrt{\frac{1}{1-x^2}}\,dx \end{align*}\]
Esta integral es impropia ya que \(\frac{1}{1-x^2}\) tiende a \(\infty\) cuando \(x\) tiende a \(\pm 1\), por lo que se tiene
\[\begin{align*} \int_{-1}^1 \sqrt{\frac{1}{1-x^2}}\,dx &= \lim_{t\to -1^+}\int_{t}^0 \sqrt{\frac{1}{1-x^2}}\,dx + \lim_{t\to 1^+}\int_0^t \sqrt{\frac{1}{1-x^2}}\,dx \\ &= -\lim_{t\to -1^+} \operatorname{arcsen}(t) + \lim_{t\to 1^+} \operatorname{arcsen}(t) = -\left(-\frac{\pi}{2}\right)+\frac{\pi}{2} = \pi \end{align*}\]
Y por tanto, la longitud de la circunferencia de radio \(1\) es el doble \(2\pi\)
8.10 Cálculo de superficies de sólidos de revolución
A partir del cálculo de la longitud de una curva plana, se puede calcular la superficie del sólido de revolución que se obtiene al girarla sobre el eje \(x\). Siguiendo con la idea de aproximar la longitud de la curva mediante polígonos, al rotar alrededor del eje \(x\) cada uno de los segmentos que forman parte del polígono, se obtiene un tronco de cono.
Para calcular la superficie del envolvente del tronco de cono, veremos primero cuál es el la superficie de este envolvente para un cono completo. Si desplegamos el envolvente de un cono completo cortándolo por su generatriz, se puede comprobar que se trata de un sector de círculo con radio la generatriz del cono \(l\) y con arco de circunferencia el perímetro del círculo de la base del cono \(2\pi r\).
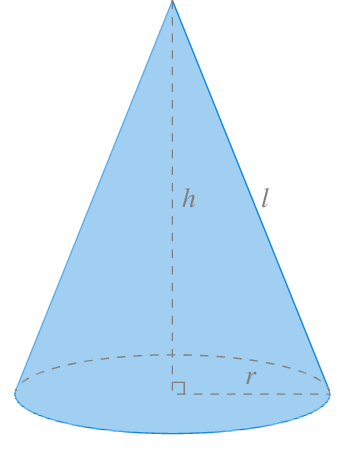
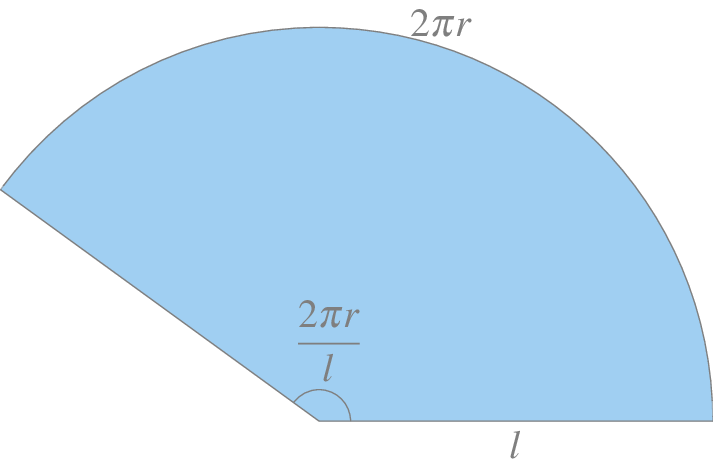
El ángulo que describe este sector de círculo es \(\theta = \frac{2\pi r}{l}\), y por tanto, su área es \(\frac{\theta}{2}l^2= \frac{2\pi r}{2l}l^2 = \pi rl\).
Para calcular ahora la superficie del envolvente del tronco de cono como del de la figura de más abajo, con radio menor \(r_1\) y radio mayor \(r_2\), basta con restar a la superficie del cono de radio \(r_2\) y generatriz \(l_2\), la superficie del cono de radio \(r_1\) y generatriz \(l_1\).
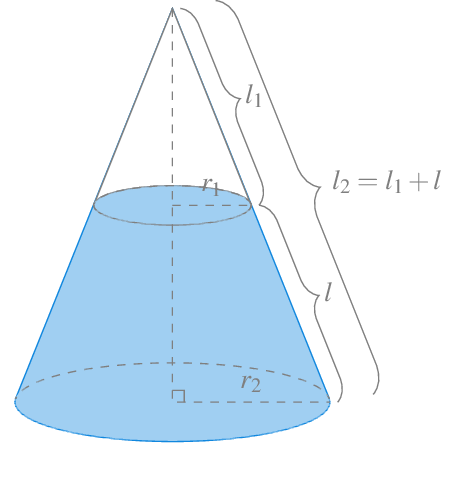
La superficie del tronco de cono es, por tanto,
\[ \pi r_2 l_2 - \pi r_1 l_1 = \pi (r_2l_2-r_1l_1) = \pi(r_2(l+l_1)-r_1l_1) = \pi ((r_2-r_1)l_1+r_2l) \]
Para poder expresar la superficie en función de \(l\), como por semejanza de triángulos rectángulos se tiene que
\[ \frac{l_1}{r_1}=\frac{l_2}{r_2}=\frac{l+l_1}{r_2} \Leftrightarrow r_2l_1 = r_1(l+l_1) \Leftrightarrow r_1l = (r_2-r_1)l_1, \]
de manera que sustituyendo en la expresión de la superficie del tronco del cono, se tiene
\[ \pi ((r_2-r_1)l_1+r_2l) = \pi (r_1l+r_2l) = \pi (r_1+r_2) l. \]
Así pues, si tomamos una partición \(P_n=\{x_0=a, x_1, \ldots, x_n=b\}\) del intervalo \([a,b]\), la superficie del tronco de cono correspondiente al subintervalo \([x_{i-1},x_i]\) es
\[ S_i = \pi (f(x_{i-1})+f(x_i))l_i, \]
donde \(l_i\) es la longitud del segmento que une los puntos \((x_{i-1},f(x_{i-1}))\) y \((x_i,f(x_i))\), que como vimos en la sección anterior, puede expresarse, gracias al teorema del valor medio, como \(\sqrt{1+f'(x'_i)^2}\) para algún \(x'_i \in [x_{i-1},x_i]\). Por tanto, la superficie del tronco de cono correspondiente al subintervalo \([x_{i-1},x_i]\) puede expresarse finalmente como
\[ S_i = \pi (f(x_{i-1})+f(x_i))\sqrt{1+f'(x'_i)^2} \] para algún \(x'_i\in [x_{i-1},x_i]\).
Si sumamos las superficies de todos los troncos de cono que se obtienen para la partición \(P_n\),
\[ \sum_{i=1}^n S_i = \sum_{i=1}^n \pi (f(x_{i-1})+f(x_i))\sqrt{1+f'(x'_i)^2}, \]
se obtiene una aproximación de la superficie del sólido de revolución generado al rotar la gráfica de la función \(f\) alrededor del eje \(x\). A medida que aumentamos el número de intervalos en la partición, la aproximación será mejor y en el límite cuanto \(n\) tiende a \(\infty\), tendremos el valor exacto de la superficie de revolución. Como ya se ha visto en las secciones anteriores, esta suma infinita es la integral de Riemann de las superficie del tronco de cono, es decir,
\[ S = \lim_{n\to\infty} \sum_{i=1}^n \pi (f(x_{i-1})+f(x_i))\sqrt{1+f'(x'_i)^2} = \int_a^b 2 \pi f(x)\sqrt{1+f'(x)^2}\,dx, \]
ya que, cuando los intervalos se hacen infinitamente pequeños, \(f(x_{i_1})\) y \(f(x_i)\) se aproximan cada vez más el uno al otro y, en el límite, acaban siendo el mismo valor \(f(x)\), por lo que en la integral se pone \(2 f(x)\).
Ejemplo 8.20 Veamos cómo calcular la superficie de una esfera de radio \(r\) centrada en el origen. Esta esfera es el sólido de revolución que surge al rotar la función \(f(x)=\sqrt{r^2-x^2}\) alrededor del eje \(x\), por lo que su superficie puede calcularse mediante la integral
\[\begin{align*} \int_{-r}^r 2 \pi f(x)\sqrt{1+f'(x)^2}\,dx &= \int_{-r}^r 2 \pi \sqrt{r^2-x^2}\sqrt{1+\left(\frac{-x}{\sqrt{r^2-x^2}}\right)^2}\,dx \\ &= \int_{-r}^r 2 \pi \sqrt{r^2-x^2}\sqrt{1+\frac{x^2}{r^2-x^2}}\,dx \\ &= \int_{-r}^r 2 \pi \sqrt{r^2-x^2}\sqrt{\frac{r^2}{r^2-x^2}}\,dx \\ &= \int_{-r}^r 2 \pi \sqrt{r^2-x^2\frac{r^2}{r^2-x^2}}\,dx \\ &= \int_{-r}^r 2 \pi \sqrt{r^2}\,dx = \int_{-r}^r 2 \pi r\,dx \\ &= 2 \pi r [x]_{-r}^r = 2\pi r(r-(-r)) = 4\pi r^2. \end{align*}\]
8.11 Aplicaciones físicas
En esta sección presentamos varias aplicaciones de las integrales en distintas áreas de la Física.
8.11.1 Cinemática
Como ya ese vió en la interpretación cinemática de la derivada, cuando \(s(t)\) es una función que describe la posición de un objeto que se mueve a lo largo del eje \(x\), \(s'(t)\) es la velocidad instantánea del objeto en cada instante \(t\) y \(s''(t)\) es la aceleración en cada instante \(t\).
Así pues, si conocemos la velocidad instantánea \(v(t)\) de un objeto en cada instante \(t\), podemos averiguar su posición integrando la velocidad. Como $s(t) es una primitiva de \(v(t)\), según el teorema fundamental del cálculo, se tiene
\[ \int_a^b v(t)\, dt = s(a)-s(b), \]
es decir, la diferencia entre la posición el objeto en los instantes \(t=b\) y \(t=a\).
La integral anterior mide el desplazamiento neto del objeto, que coincide con el desplazamiento absoluto si la función velocidad es positiva en el intervalo de integración, pero si toma valores positivos y negativos, para calcular la distancia total recorrida por el objeto en el intervalo \([a, b]\), es necesario integrar el valor absoluto de la velocidad, tal y como se hizo para el cálculo de áreas en la Sección 8.6.1.
En general, suponiendo que el instante inicial en el que comienza el movimiento es el instante \(t=0\), y por tanto, la posición inicial del objeto es \(s(0)\), la posición que ocupa el objeto en cualquier instante \(t\) viene dada por la integral
\[ s(t) = s(0) + \int_{0}^t v(x)\,dx. \]
Del mismo modo, si conocemos la aceleración del objeto \(a(t)\) en cada instante \(t\), podemos averiguar su velocidad integrando la aceleración. Como \(v(t)\) es una primitiva de \(a(t)\), según el teorema fundamental del cálculo, se tiene
\[ \int_a^b a(t)\, dt = v(t_1)-v(t_0), \]
es decir, la diferencia entre la velocidades en los instantes \(a\) y \(b\).
Si suponemos como antes, que el instante inicial en el que comienza el movimiento es el instante \(t=0\), y por tanto, la velocidad inicial del objeto es \(v(0)\), la velocidad del objeto en cualquier instante \(t\) viene dada por la integral
\[ v(t) = v(0) + \int_{0}^t a(x)\,dx. \]
Combinando estos dos resultados, es posible averiguar la posición que ocupa el objeto si es conoce su aceleración.
Ejemplo 8.21 Veamos cómo podemos deducir la famosa fórmula de la posición de un objeto en caída libre. En este caso, supondremos que la posición inicial del objeto es \(s(0)=s_0\) m y su velocidad inicial es \(v(0)=v_0\) m/s. Además, supondremos que no hay rozamiento, por lo que la única fuerza que actúa sobre el objeto es la gravedad, con una aceleración constante \(g=9.8\) m/s\(^2\).
Integrando la aceleración obtenemos la velocidad del objeto en cada instante \(t\).
\[ v(t) = v(0) + \int_{0}^t -g\,dx = v_0 -g [x]_0^t = v_0-gt \]
Ahora, integrando la velocidad obtenemos la posición el objeto en cada instante \(t\).
\[ s(t) = s(0) + \int_{0}^t v_0-gx\,dx = s_0 + \left[v_0 x-g\frac{x^2}{2}\right]_0^t = s_0+v_0 t-g\frac{t^2}{2}. \]
En el caso de que la posición inicial sea \(s_0=0\) m, y se parta de una situación de reposo, es decir, \(v_0=0\) m/s, se llega a
\[ s(t) = -g\frac{t^2}{2}. \]
8.11.2 Trabajo
Otra aplicación importante de las integrales en Física es el cálculo del trabajo realizado al desplazar un objeto aplicándole una fuerza. En mecánica clásica, si un objeto se desplaza en línea recta y su posición viene dada por la función \(s(t)\), la fuerza \(F\) ejercida sobre el objeto viene dada por la segunda ley de Newton
\[ F = m\cdot a \]
donde \(m\) es la masa del objeto y \(a\) es la aceleración.
La unidad de medida de la fuerza en el Sistema Internacional (SI) es el newton N=kg\(\cdot\) m /s\(^2\), es decir, si se aplica \(1\) N a un objeto de masa \(1\) kg, este sufrirá una aceleración de \(1\) m/s\(^2\).
Cuando se aplica una fuerza sobre un objeto desplazándolo en línea recta una determinada distancia, el trabajo \(W\) realizado en ese desplazamiento viene dado por el producto de la fuerza y la distancia que recorre el objeto, es decir,
\[ W = F\cdot d \]
Como la fuerza se mide en newtons, la unidad del trabajo en el SI es el julio \(J = N\cdot m\).
Cuando la fuerza es constante, el trabajo es proporcional a la distancia recorrida.
Ejemplo 8.22 Si levantamos una pesa de 1 kg desde el suelo hasta una altura de 2 m, la fuerza ejercida es igual y opuesta a la que ejerce la gravedad, es decir,
\[ F = m\cdot g = 1 \mbox{ kg} \cdot 9.81 \mbox{ m/s$^2$} = 9.8 \mbox{ N}, \]
y el trabajo realizado es
\[ W = F\cdot d = 9.81 \mbox{ N} \cdot 2 \mbox{ m} = 19.62 \mbox{ J} \]
Cuando la fuerza que se aplica sobre el objeto no es constante, sino que viene dada por una función \(f(x)\), el cálculo no es tan sencillo, pero podemos aplicar la misma estrategia utilizada con las sumas de Riemann. Si se quiere calcular el trabajo realizado al desplazar el objeto desde la posición \(x=a\) hasta \(x=b\) aplicando una fuerza \(f(x)\), podemos tomar una partición \(P_n=\{x_0=a, x_1, \ldots, x_n=b\}\) de \(n\) intervalos de igual amplitud \(\Delta x\) y aproximar el trabajo realizado en el intervalo \([x_{i-1},x_i]\) con \(W_i= f(x'_i)(x_i-x_{i-1}) = f(x'_i)\Delta x\), donde \(x'_i\) es cualquier valor del intervalo \([x_{i-1},x_i]\). De este modo, el trabajo realizado en el intervalo \([a,b]\) puede aproximarse mediante la suma
\[ W = \sum_{i=1}^n W_i = \sum_{i=1}^n f(x'_i)\Delta x. \]
Como ya se ha visto, cuando el número de subintervalos tiende a \(\infty\), en el límite, si la función \(f\) es integrable Riemann, podemos obtener el trabajo exacto realizado con la integral
\[ \int_a^b f(x)\,dx \]
La integral anterior mide el trabajo realizado al aplicar una fuerza en el sentido del desplazamiento, es decir, cuando es positiva.
Ejemplo 8.23 La función \(f(x)=\frac{1}{1+x}\) determina la fuerza que actúa sobre una partícula situada a una distancia \(x\) del origen de coordenadas. El trabajo que se realiza al desplazar la partícula desde el origen al punto \(1\) es
\[ W = \int_0^1 \frac{1}{1+x}\,dx = [\ln(1+x)]_0^1 = \ln(2) \mbox{ J}. \]
8.11.3 Centro de masas
El centro de masas de un objeto o sistema de objetos es el punto geométrico que dinámicamente se comporta como si en él estuvieran aplicadas las fuerzas que actúan sobre el objeto. En el caso de un sistema discreto, como por ejemplo una palanca sobre la que se coloca un número finito de pesos, como en la figura de más abajo, determinar el centro de gravedad es sencillo, ya que basta aplicar la ley de la palanca de Arquímedes, que establece
\[ m_1d_1 = m_2d_2 \]
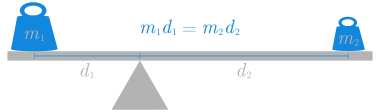
Si colocamos las dos masas \(m_1\) y \(m_2\) sobre el eje \(x\) en las posiciones \(x_1\) y \(x_2\) respectivamente, el centro de masas \(\bar x\), que se correspondería con la posición donde habría que poner el punto de apoyo de la palanca para que las dos masas la equilibraran, se puede calcular aplicando la ley de la palanca,
\[ m_1(\bar x-x_1) = m_2(x_2-\bar x) \Leftrightarrow \bar x = \frac{m_1x_1+m_2x_2}{m_1+m_2}, \]
que, en realidad, es la media de las posiciones de \(x_1\) y \(x_2\) ponderada de las masas.
Debido a la fuerza de la gravedad, cada objeto ejerce una fuerza sobre la palanca que tiende a rotarla alrededor del punto de apoyo (si el objeto está a la izquierda del punto de apoyo provocará una rotación en sentido antihorario, mientras que si está a la derecha lo hará en sentido horario). Esta efecto de rotación se conoce como momento o torque, y para un objeto de masa \(m\) colocado en la posición \(x\) de la palanca, toma el valor \(m\cdot x\cdot g\), y sus unidades en el sistema internacional son \(N\cdot m\) (aunque ya hemos visto que \(N\cdot m\) son julios, en este caso las unidades de los momentos no se expresan en julios para distinguirlos del trabajo, ya que el trabajo es una magnitud escalar, mientras que el momento es una magnitud vectorial).
En general, si hay \(n\) objetos sobre la balanza, el centro de masas se alcanzará en el punto \(\bar x\) que cumpla,
\[ \sum_{i=1}^n m_i(x_i-\bar x) = 0 \Leftrightarrow \bar x = \frac{\sum_{i=1}^n m_ix_i}{\sum_{i=1}^n m_i}. \]
8.11.3.1 Centro de masas de una varilla con densidad variable
Cuando el sistema contiene infinitos objetos de distintas masas, o se trata de un objeto con una densidad variable, la cosa se complica. Por ejemplo si queremos calcular el centro de masas de una varilla metálica sobre un intervalo \([a,b]\), tal que su densidad viene dada por la función \(f(x)\) kg/m, se puede descomponer el intervalo \([a,b]\) en \(n\) subintervalos de igual amplitud mediante una partición \(P_n=\{x_0=a, x_1, \ldots, x_n=b\}\), con \(\Delta x=x_i-x_{i-1}\) \(i=1, \ldots, n\). Podemos aproximar la masa de cada subintervalo, asumiendo que tuviese una densidad constante \(f(x_i)\), como \(m_i = f(x_i)(x_i-x_{i-1}) = f(x_i) \Delta x\), y por tanto,su momento será \(x_im_i = x_i f(x_i)\Delta x\). De este modo, el centro de masas de la varilla será aproximadamente, según la fórmula anterior,
\[ \bar x = \frac{\sum_{i=1}^n m_ix_i}{\sum_{i=1}^n m_i} = \frac{\sum_{i=1}^n x_if(x_i)\Delta x}{\sum_{i=1}^n f(x_i)\Delta x}, \]
que es el cociente de dos sumas de Riemann. De nuevo, si aumentamos el número de subintervalos, cuando \(n\) tiende a \(\infty\), en el límite se obtiene el valor exacto del centro de masas mediante el cociente de dos integrales definidas
\[ \bar x = \frac{\int_a^b xf(x)\,dx}{\int_a^b f(x)\,dx} \]
Ejemplo 8.24 El centro de masas de una varilla situada sobre el intervalo \([5, 10]\) con una densidad en cada punto \(x\) dada por la función \(f(x)=2x-1\) es
\[\begin{align*} \bar x &= \frac{\int_5^{10} xf(x)\,dx}{\int_5^{10} f(x)\,dx} = \frac{\int_5^{10} x(2x-1)\,dx}{\int_5^{10} 2x-1\,dx} \\ &= \frac{\left[2\frac{x^3}{3}-\frac{x^2}{2}\right]_5^{10}}{[x^2-x]_5^{10}} = \frac{\left(2\frac{10^3}{3}-\frac{10^2}{2}-2\frac{5^3}{3}+\frac{5^2}{2}\right)}{10^2-10-5^2+5} \\ &= \frac{3275/6}{70} = 7.7976. \end{align*}\]
8.11.3.2 Centro de masas de una región plana con densidad fija
Cuando se tiene una región plana en \(\mathbb{R}^2\), su centro de masas se conoce como centroide y sus coordenadas se representan como \((\bar x, \bar y)\). El cálculo de las coordenadas del centroide, cuando todos los puntos de la región plana tienen la misma densidad \(\delta\), se puede realizar de forma similar al cálculo del centro de masas de una varilla con densidad variable.
Si la región está delimitada por una función \(f(x)\) y el eje \(x\) en un intervalo \([a,b]\), al descomponer el intervalo \([a,b]\) en \(n\) subintervalos de igual amplitud mediante una partición \(P_n=\{x_0=a, x_1, \ldots, x_n=b\}\), con \(\Delta x=x_i-x_{i-1}\) \(i=1, \ldots, n\), se puede tomar como aproximación del área correspondiente a cada subintervalo \([x_{i-1},x_i]\) el rectángulo con base el intervalo y altura el valor de la función en el punto medio del intervalo. Si llamamos al punto medio del subintervalo \(i\)-ésimo subintervalo \(\bar x_i=\frac{x_{i-1}+x_i}{2}\), el área del rectángulo correspondiente es \(A_i = f(\bar x_i)\Delta x\) y su masa \(M_i = \delta f(\bar x_i)\Delta x\). Como todos los puntos tienen la misma densidad \(\delta\), el centroide del rectángulo \(i\)-ésimo es \((\bar x_i, \frac{1}{2}f(\bar x_i))\).
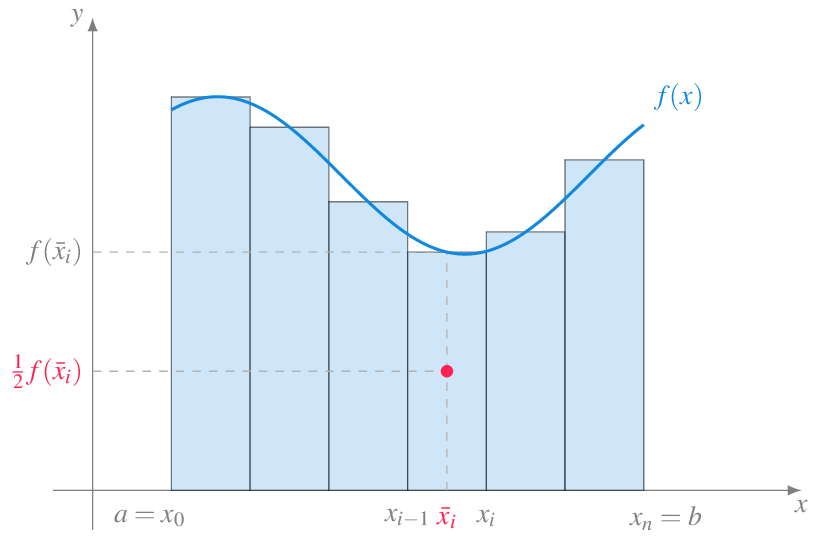
El momento del rectángulo \(i\)-ésimo con respecto al eje \(y\) es
\[ \bar x_i M_i = x_i \delta f(\bar x_i)\Delta x \]
de manera que podemos aproximar el momento de la región con respecto al eje \(y\) mediante la suma de Riemann
\[ \sum_{i=1}^n x_i \delta f(\bar x_i)\Delta x = \delta \sum_{i=1}^n x_i f(\bar x_i)\Delta x, \]
y, tomando particiones cada vez con más subintervalos, en el límite cuanto \(n\) tiende a \(\infty\) se obtiene el momento de la región con respecto al eje \(y\) mediante la integral definida
\[ \delta \lim_{n\to \infty}\sum_{i=1}^n x_i f(\bar x_i)\Delta x = \delta \int_a^b x f(x)\, dx, \]
por lo que se tiene
\[ \bar x = \frac{\delta \int_a^b x f(x)\, dx,}{\delta \int_a^b f(x)\, dx,} = \frac{\int_a^b x f(x)\, dx,}{\int_a^b f(x)\, dx,} \]
Del mismo modo, el momento del rectángulo \(i\)-ésimo con respecto al eje \(x\) es
\[ \frac{1}{2}f(\bar x_i) M_i = \frac{1}{2}f(\bar x_i) \delta f(\bar x_i)\Delta x = \frac{1}{2}\delta f(\bar x_i)^2\Delta x \]
de manera que podemos aproximar el momento de la región con respecto al eje \(x\) mediante la suma de Riemann
\[ \sum_{i=1}^n \frac{1}{2}\delta f(\bar x_i)^2\Delta x = \frac{1}{2}\delta \sum_{i=1}^n f(\bar x_i)^2\Delta x, \]
y, tomando particiones cada vez con más subintervalos, en el límite cuanto \(n\) tiende a \(\infty\) se obtiene el momento de la región con respecto al eje \(x\) mediante la integral definida
\[ \frac{1}{2}\delta \lim_{n\to \infty}\sum_{i=1}^n f(\bar x_i)^2\Delta x = \frac{1}{2}\delta \int_a^b f(x)^2\, dx, \]
por lo que se tiene
\[ \bar y = \frac{\frac{1}{2}\delta \int_a^b f(x)^2\, dx,}{\delta \int_a^b f(x)\, dx,} = \frac{\int_a^b f(x)^2\, dx,}{2\int_a^b f(x)\, dx,} \]
Ejemplo 8.25 Veamos cómo calcular el centroide del semicírculo de ecuación \(f(x)=\sqrt{1-x^2}\). En primer lugar calculamos el área del semicírculo. Haciendo el cambio de variable \(x=\operatorname{sen}(\theta)\), \(dx = \cos(\theta)d\theta\), se tiene
\[\begin{align*} \int_{-1}^1 f(x)\,dx &= \int_{-1}^1 \sqrt{1-x^2}\,dx = \int_{-\pi/2}^{\pi/2} \sqrt{1-\operatorname{sen}(\theta)^2}\cos(\theta)\,d\theta \\ &= \int_{-\pi/2}^{\pi/2} \sqrt{\cos(\theta)^2}\cos(\theta)\,d\theta = \int_{-\pi/2}^{\pi/2} \cos(\theta)^2\,d\theta \\ &= \int_{-\pi/2}^{\pi/2} \frac{1+\cos(\theta)}{2}\,d\theta = \frac{1}{2}\left[\theta + \frac{1}{2}\operatorname{sen}(2\theta) \right]_{-\pi/2}^{\pi/2} \\ &= \frac{1}{2}\left(\frac{\pi}{2}+\frac{1}{2}\operatorname{sen}(\pi)+\frac{\pi}{2}-\frac{1}{2}\operatorname{sen}(-\pi)\right)\\ &= \frac{1}{2}\left(\frac{\pi}{2}+\frac{\pi}{2}\right) = \frac{\pi}{2}. \end{align*}\]
Y ahora calculamos el momento con respecto al eje \(y\).
\[\begin{align*} \int_{-1}^1 xf(x)\,dx &= \int_{-1}^1 x\sqrt{1-x^2}\,dx = \int_{-\pi/2}^{\pi/2} \operatorname{sen}(\theta)\sqrt{1-\operatorname{sen}(\theta)^2}\cos(\theta)\,d\theta \\ &= \int_{-\pi/2}^{\pi/2} \operatorname{sen}(\theta)\sqrt{\cos(\theta)^2}\cos(\theta)\,d\theta = \int_{-\pi/2}^{\pi/2} \operatorname{sen}(\theta)\cos(\theta)^2\,d\theta \\ &= \left[\frac{\cos(\theta)^3}{3} \right]_{-\pi/2}^{\pi/2} = \frac{1}{3}(\cos(\pi/2)^3-\cos(-\pi/2)^3) = 0. \end{align*}\]
De manera que
\[ \bar x = \frac{\int_{-1}^1 x f(x)\, dx,}{\int_{-1}^1 f(x)\, dx,} = \frac{0}{\pi/2} = 0 \]
Finalmente calculamos el momento con respecto al eje \(x\).
\[\begin{align*} \frac{1}{2}\int_{-1}^1 f(x)^2\,dx &= \frac{1}{2}\int_{-1}^1 \sqrt{1-x^2}^2\,dx = \frac{1}{2}\int_{-1}^1 1-x^2\,dx = \frac{1}{2}\left[x - \frac{x^3}{3}\right]_{-1}^1 \\ &= \frac{1}{2}\left(1-\frac{1^3}{3}-(-1)+\frac{(-1)^3}{3}\right) = \frac{1}{2}\frac{4}{3} = \frac{4}{6}. \end{align*}\]
y
\[ \bar y = \frac{1}{2}\frac{\int_{-1}^1 f(x)^2\, dx,}{\int_{-1}^1 f(x)\, dx,} = \frac{4/6}{\pi/2} = \frac{4}{3\pi}. \]
Luego el centroide es \(\left(0, \frac{4}{3\pi}\right)\).
8.12 Aplicaciones estadísticas
Veremos a continuación otras aplicaciones de la integral más relacionadas con la Estadística.
8.12.1 Cálculo de la media de una función
Resulta sencillo calcular la media de un conjunto finito de números, pero la cosa se complica cuando el conjunto de números es infinito, como por ejemplo, cuando queremos calcular la temperatura media de un día.
En esta sección veremos cómo calcular el valor medio de una función \(f\) en un intervalo \([a,b]\), siempre y cuando la función sea integrable en el intervalo. La estrategia que seguiremos será la de siempre. Tomaremos una partición \(P_n=\{x_0=a, x_1, \ldots, x_n=b\}\) de \(n\) intervalos de igual amplitud \(\Delta x = \frac{b-a}{n}\) y aproximar el valor medio de la función mediante la suma finita
\[ \sum_{i=1}^n \frac{f(x'_i)}{n} = \sum_{i=1}^n \frac{f(x'_i)}{\frac{b-a}{\Delta x}} = \frac{1}{b-a}\sum_{i=1}^n f(x'_i)\Delta x, \]
donde \(x'_i\) es cualquier valor del intervalo \([x_{i-1},x_i]\).
Cuando el número de subintervalos tiende a \(\infty\), la suma anterior se parecerá cada vez más al verdadero valor medio de la función en el intervalo, y en el límite, si la función \(f\) es integrable Riemann, se puede obtener el valor medio de la función mediante la integral definida
\[ \bar f[a,b] = \frac{1}{b-a}\int_a^b f(x)\,dx \]
Ejemplo 8.26 El valor medio de la función \(f(x)=\operatorname{sen}(x)\) en el intervalo \([0,\pi/2]\) es
\[\begin{align*} \bar f[0,\pi/2] &= \frac{1}{\pi/2} \int_0^{\pi/2} f(x)\, dx = \frac{1}{\pi/2} \int_0^{\pi/2} \operatorname{sen}(x)\, dx \\ &= \frac{2}{\pi}[-\cos(x)]_0^{\pi/2} = \frac{2}{\pi}(0+1) = \frac{2}{\pi} \end{align*}\]
Y el valor medio de esta misma función en el intervalo \([0,\pi]\) es
\[\begin{align*} \bar f[0,\pi] &= \frac{1}{\pi} \int_0^{\pi} f(x)\, dx = \frac{1}{\pi} \int_0^{\pi} \operatorname{sen}(x)\, dx \\ &= \frac{2}{\pi}[-\cos(x)]_0^{\pi} = \frac{2}{\pi}(-1+1) = 0, \end{align*}\]
porque la función seno es positiva en \([0,\pi/2]\) y negativa en \([\pi/2, \pi]\), de manera que los valores positivos se compensan con los negativos y se obtiene una media 0.
8.12.2 Cálculo de probabilidades
En Estadística, para modelar la distribución de valores de una variable aleatoria continua se utiliza la función de densidad de probabilidad, que es una función \(f(x)\) que cumple las siguientes propiedades
\(f\) es no negativa, es decir, \(f(x)\geq 0\) para todo \(x\) en el dominio de la variable aleatoria.
El área total comprendida entre la gráfica de \(f\) y el eje \(x\) es 1, es decir,
\[ \int_{-\infty}^{\infty} f(x)\,dx = 1. \]
La probabilidad de que la variable aleatoria tome un valor en un intervalo \([a,b]\) es es el área comprendida entre la gráfica de \(f\) y el eje \(x\) en ese intervalo, es decir,
\[ P(a\leq X\leq b) = \int_a^b f(x)\,dx \]
Ejemplo 8.27 La función \(f(x)=\frac{9-x^2}{36}\) es una función de densidad de probabilidad para \(x\in[-3,3]\), ya que es no negativa en ese intervalo y se cumple >
\[ \int_{-3}^{3} \frac{9-x^2}{36}\,dx = \frac{1}{36}\left[9x-\frac{x^3}{3}\right]_{-3}^{3} = \frac{1}{36}(27 - 9 + 27 - 9) = 1. \]
Por tanto, la probabilidad de que la variable aleatoria correspondiente tome un valor en el intervalo \([0,2]\) es
\[ P(0\leq X\leq 2) = \int_0^2 \frac{9-x^2}{36}\,dx = \frac{1}{36}\left[9x-\frac{x^3}{3}\right]_0^2 = \frac{1}{36}(18 - \frac{8}{3}) = \frac{23}{54}\approx 0.4259. \]
8.12.3 Cálculo de estadísticos
El cálculo de estadísticos de una variable aleatoria continua, como la media, la varianza, la mediana, etc., también se realiza mediante integrales. Por ejemplo, la media de una variable aleatoria \(X\) con función de densidad de probabilidad \(f(x)\) se calcula mediante la integral
\[ E(X) = \int_{-\infty}^{\infty} x f(x)\,dx, \]
y la varianza mediante la integral
\[ \operatorname{Var}(X) = E(X^2) - E(X)^2 = \int_{-\infty}^{\infty} x^2 f(x)\,dx - \left(\int_{-\infty}^{\infty} x f(x)\,dx\right)^2, \]
mientras que la mediana es el valor \(Me\) que deja acumulada la mitad de la probabilidad total, y por tanto cumple
\[ P(X\leq Me) = \int_{-\infty}^{Me} f(x)\,dx = \frac{1}{2}. \]
Ejemplo 8.28 La media de la variable aleatoria con función de densidad de probabilidad \(f(x)=\frac{9-x^2}{36}\) es
\[\begin{align*} E(X) &= \int_{-3}^{3} x \frac{9-x^2}{36}\,dx = \frac{1}{36}\int_{-3}^{3} 9x-x^3\,dx \\ &= \frac{1}{36}\left[\frac{9x^2}{2}-\frac{x^4}{4}\right]_{-3}^{3} = \frac{1}{36}\left(\frac{81}{2}-\frac{81}{4}-\frac{81}{2}+\frac{81}{4}\right) = 0. \end{align*}\]
La varianza es
\[\begin{align*} \operatorname{Var}(X) &= E(X^2) - E(X)^2 = \int_{-3}^{3} x^2 \frac{9-x^2}{36}\,dx - 0^2 \\ &= \frac{1}{36}\int_{-3}^{3} 9x^2-x^4\,dx = \frac{1}{36}\left[\frac{9x^3}{3}-\frac{x^5}{5}\right]_{-3}^{3} \\ &= \frac{1}{36}\left(\frac{243}{3}-\frac{243}{5}+\frac{243}{3}-\frac{243}{5}\right) = \frac{9}{5} \approx 1.8. \end{align*}\]
Finalmente, la mediana es
\[\begin{align*} P(X\leq Me) &= \int_{-3}^{Me} \frac{9-x^2}{36}\,dx = \frac{1}{36}\left[9x-\frac{x^3}{3}\right]_{-3}^{Me} \\ &= \frac{1}{36}\left(9Me-\frac{Me^3}{3}+27-\frac{27}{3}\right) \\ &= \frac{1}{36}\left(9Me-\frac{Me^3}{3}+18\right) = \frac{1}{2},\\ & \Rightarrow 9Me-\frac{Me^3}{3}+18 = 18,\\ & \Rightarrow 9Me-\frac{Me^3}{3} = 0,\\ & \Rightarrow Me\left(9-\frac{Me^2}{3}\right) = 0,\\ & \Rightarrow Me = 0 \mbox{ o } Me = \sqrt{27},\\ \end{align*}\]
pero \(\sqrt{27}\) no está en el intervalo \([-3,3]\), por lo que la mediana es 0.