1 Teoría de conjuntos

Los conjuntos son entes matemáticos que se usan habitualmente para modelar situaciones reales en las que aparecen colecciones de objetos de cualquier naturaleza, así como las relaciones entre ellos, y por tanto, aparecen en la mayor parte de los problemas de Ciencia o Ingeniería.

Al mismo tiempo, los conjuntos son una de las estructuras matemáticas más básicas sobre las que se construyen la mayoría de las teorías matemáticas.

En este capítulo se estudia el concepto de conjunto y sus principales propiedades y relaciones.

1.1 Conjuntos

Definición 1.1 (Conjunto) Un conjunto es a una colección o agrupación bien definida de objetos que puede considerarse en sí misma otro objeto. Para representar un conjunto se indican sus elementos entre llaves y normalmente se utilizarán letras mayúsculas para referirse a ellos.

Ejemplo 1.1 Algunos ejemplos de conjuntos son:

El conjunto de los días de la semana es \(A = \{\mbox{L, M, X, J, V, S, D}\}\).
El conjunto de los colores básicos es \(B = \{\mbox{rojo, verde, azul}\}\).
El conjunto de los puntos de un dado \(C = \{ 1, 2, 3, 4, 5, 6 \}\).
El conjunto de los números naturales pares: \(D = \{2, 4, 6, \ldots \}\).

Definición 1.2 (Elementos) Los objetos que componen un conjunto se llaman elementos o miembros del conjunto.

Los elementos de un conjunto pueden ser cualquier cosa (días, colores, personas, etc), pero en este curso nos centraremos los conjuntos numéricos, es decir, los conjuntos cuyos elementos son números, ya que son los que se estudian en el Análisis Matemático.

Existen dos formas de definir un conjunto: por extensión o por comprensión. La definición extensiva consiste en listar de manera explícita todos sus elementos, como por ejemplo \(\{1, 2, 3\}\), mientras que la intensiva o por comprensión, consiste en dar una propiedad que cumplen los elementos del conjunto y solo ellos, como por ejemplo el conjunto de los números naturales menores que \(4\). En este último caso se suele utilizar la notación \(\{x: P(x)\}\), donde \(P(x)\) es la propiedad que cumple \(x\).

Mientras que las definiciones por extensión no presentan problemas, hay que tener cuidado con las definiciones por comprensión, pues no todas las propiedades definen conjuntos válidos, tal y como demostró Bertrand Russell con su famosa paradoja del barbero.

Definición 1.3 (Pertenencia) Si \(a\) es un elemento de un conjunto \(A\), se dice que \(a\) pertenence a \(A\) y se denota \(a\in A\). Por el contrario, si \(a\) no es un elemento del conjunto \(A\), se dice que no pertenece a \(A\) y se denota \(a\not \in A\).

Ejemplo 1.2 Si \(A\) es el conjunto de los números naturales pares, \(2\in A\), pero \(1\not \in A\).

Definición 1.4 (Igualdad) Se dice que dos conjuntos \(A\) y \(B\) son iguales, y se denota \(A=B\), si tienen exactamente los mismos elementos. En caso contrario se escribe \(A\neq B\).

Conviene remarcar que en un conjunto no puede haber elementos repetidos y tampoco importa el orden en que se listan los elementos.

Ejemplo 1.3 \(\{1, 2, 3\} = \{3, 1, 2\}\).

Proposición 1.1 La igualdad de conjuntos es una relación de equivalencia, es decir, satisface las propiedades:

Reflexiva: \(A = A\).
Simétrica: Si \(A = B\) entonces \(B = A\).
Transitiva: \(A = B\) y \(B = C\), entonces \(A = C\).

Definición 1.5 (Subconjunto) Se dice que un conjunto \(A\) es un subconjunto o está incluído en otro conjunto \(B\), y se denota \(A \subseteq B\), si todos los elementos de \(A\) pertenecen a \(B\), es decir, \[ \forall x \in A, x\in B \]

Cuando \(A\subseteq B\) pero \(A\neq B\) se dice que \(A\) está estríctamente incluido en \(B\) o que \(A\) es un subconjunto propio de \(B\) y se escribe \(A\subsetneq B\).

Ejemplo 1.4 \(\{1, 2, 3\} \subseteq \{3, 1, 2\}\) y \(\{1, 3\} \subsetneq \{3, 1, 2\}\).

Proposición 1.2 La inclusión de conjuntos es una relación de orden parcial, es decir, satisface las propiedades:

Reflexiva: \(A \subseteq A\).
Antisimétrica: Si \(A \subseteq B\) y \(B \subseteq A\), entonces \(A = B\).
Transitiva: \(A \subseteq B\) y \(B \subseteq C\), entonces \(A \subseteq C\).

Definición 1.6 (Conjunto vacío) El conjunto que no tiene ningún elemento se llama conjunto vacío y se denota \(\emptyset\).

1.2 Álgebra de conjuntos

A continuación se definen las principales operaciones sobre conjuntos y sus propiedades.

Definición 1.7 (Unión) Dados dos conjuntos \(A\) y \(B\), se llama unión de \(A\) y \(B\), y se denota \(A\cup B\), al conjunto de todos los elementos que pertenecen al menos a uno de los conjuntos \(A\) y \(B\).

\[A\cup B = \{x\,:\, x\in A\mbox{ o }x\in B\}.\]

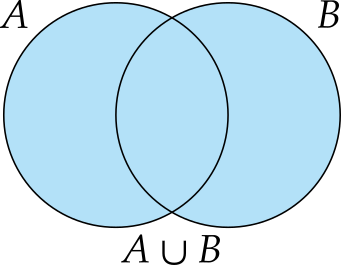
Ejemplo 1.5 Dado el conjunto de los números que contiene un dado, \(\Omega=\{1,2,3,4,5,6\}\) y sus subconjuntos \(A=\{2,4,6\}\) y \(B=\{1,2,3,4\}\),la unión de \(A\) y \(B\) es \(A\cup B=\{1,2,3,4,6\}\).

Definición 1.8 (Intersección) Dados dos conjuntos \(A\) y \(B\), se llama intersección de \(A\) y \(B\), y se denota \(A\cap B\), al conjunto de todos los elementos comunes a \(A\) y \(B\).

\[A\cap B = \{x\,:\, x\in A\mbox{ y }x\in B\}.\]

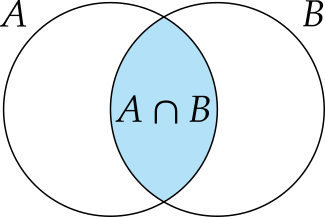
Ejemplo 1.6 Dado el conjunto de los números que contiene un dado, \(\Omega=\{1,2,3,4,5,6\}\) y sus subconjuntos \(A=\{2,4,6\}\) y \(B=\{1,2,3,4\}\),la intersección de \(A\) y \(B\) es \(A\cap B=\{2,4\}\).

Definición 1.9 (Complemento) Dado un conjunto \(A\subset \Omega\), se llama complemento de \(A\) con respecto a \(\Omega\), y se denota \(\overline A\), al conjunto de todos los elementos de \(\Omega\) que no pertenecen a \(A\).

\[\overline A = \{x\in \Omega\,:\, x\not\in A\}.\]

Ejemplo 1.7 Dado el conjunto de los números que contiene un dado, \(\Omega=\{1,2,3,4,5,6\}\) y sus subconjuntos \(A=\{2,4,6\}\) y \(B=\{1,2,3,4\}\), el contrario de \(A\) con respecto a \(\Omega\) es \(\overline A=\{1,3,5\}\), y el de \(B\) es \(\overline B = \{5, 6\}\).

Definición 1.10 (Diferencia) Dados dos conjuntos \(A\) y \(B\), se llama diferencia de \(A\) y \(B\), y se denota \(A-B\), al conjunto formado por los elementos de \(A\) que no pertenecen a \(B\), es decir,

\[A-B = \{x\,:\, x\in A\mbox{ y }x\not\in B\}.\]

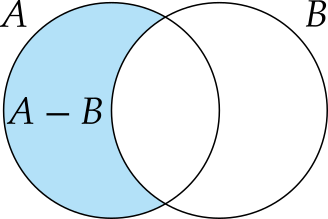
Ejemplo 1.8 Dado el conjunto de los números que contiene un dado, \(\Omega=\{1,2,3,4,5,6\}\) y sus subconjuntos \(A=\{2,4,6\}\) y \(B=\{1,2,3,4\}\),la diferencia de \(A\) y \(B\) es \(A-B=\{6\}\), y la diferencia de \(B\) y \(A\) es \(B-A=\{1,3\}\).

Definición 1.11 (Diferencia simétrica) Dados dos conjuntos \(A\) y \(B\), se llama diferencia simétrica de \(A\) y \(B\), y se denota \(A\triangle B\), al conjunto formado por los elementos que pertenecen a \(A\) o \(B\), pero no a ambos a la vez, es decir,

\[\begin{align*} A\triangle B &= \{x\,:\, x\in A-B\mbox{ o }x\in B-A\}\\ &= (A-B) \cup (B-A) = (A\cup B)-(A\cap B) \end{align*}\]

Ejemplo 1.9 Dado el conjunto de los números que contiene un dado, \(\Omega=\{1,2,3,4,5,6\}\) y sus subconjuntos \(A=\{2,4,6\}\) y \(B=\{1,2,3,4\}\),la diferencia simétrica de \(A\) y \(B\) es \(A\triangle B = \{1, 3, 6\}\).

Proposición 1.3 Dado un conjunto universo \(\Omega\) y los conjuntos \(A,B,C\subseteq \Omega\), se cumplen las siguientes propiedades:

Idempotencia: \(A\cup A=A\) y \(A\cap A=A\).
Conmutativa: \(A\cup B=B\cup A\) y \(A\cap B = B\cap A\).
Asociativa: \((A\cup B)\cup C = A\cup (B\cup C)\) y \((A\cap B)\cap C = A\cap (B\cap C)\).
Distributiva: \((A\cup B)\cap C = (A\cap C)\cup (B\cap C)\) y \((A\cap B)\cup C = (A\cup C)\cap (B\cup C)\).
Elemento neutro: \(A\cup \emptyset=A\) y \(A\cap \Omega=A\).
Elemento absorvente: \(A\cup \Omega=\Omega\) y \(A\cap \emptyset=\emptyset\).
Elemento simétrico complementario: \(A\cup \overline A = E\) y \(A\cap \overline A= \emptyset\).
Doble complemento: \(\overline{\overline A} = A\).
Leyes de Morgan: \(\overline{A\cup B} = \overline A\cap \overline B\) y \(\overline{A\cap B} = \overline A\cup \overline B\).
\(A\cap B\subseteq A\cup B\).
\(A-B = A \cap \overline B\).
\(A-B\subseteq A\) y \(B-A\subseteq B\).
\(A\triangle B = (A\cup B) - (A\cap B)\).
\(\overline \Omega = \emptyset\) y \(\overline \emptyset = \Omega\).

Definición 1.12 (Conjuntos disjuntos) Dados dos conjuntos \(A\) y \(B\), se dice que son disjuntos si no tienen ningún elemento en común, es decir, \(A\cap B=\emptyset\).

Ejemplo 1.10 Dado el conjunto de los números que contiene un dado, \(\Omega=\{1,2,3,4,5,6\}\), y sus subconjuntos \(A=\{2,4,6\}\), \(B=\{1,2,3,4\}\) y \(C=\{3, 5\}\), se tiene que \(A\) y \(B\) no son disjuntos ya que \(A\cap B=\{2, 4\}\neq \emptyset\), pero \(A\) y \(C\) son disjuntos pues \(A\cap C=\emptyset\).

Definición 1.13 (Conjunto potencia) Dado un conjunto \(A\), se llama conjunto potencia o conjunto de las partes de \(A\), y se denota \(\mathcal{P}(A)\), al conjunto de todos los subconjuntos de \(A\), es decir,

\[\mathcal{P}(A) = \{ X \, : \, X \subseteq A \}\]

Ejemplo 1.11 El conjunto potencia del conjunto \(A=\{1, 2, 3\}\) es

\[\mathcal{P}(A)=\{\emptyset, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}\}\]

1.3 Relaciones entre conjuntos

Definición 1.14 (Par ordenado) Dados dos elementos \(a\) y \(b\) se define el par ordenado \((a,b)\) como \[ (a,b) = \{\{a\}, \{a,b\}\} \]

De manera más general, se define una \(n\)-tupla ordenada como \[(a_1, a_2, \ldots, a_n) = ((a_1, a_2, \ldots, a_{n-1}), a_n)\]

De forma mas informal, decimos que \((a,b)\) es un par ordenado si el primer elemento (\(a\)) se distingue del segundo elemento (\(b\)). Por eso, se tiene que \((a,b) \neq (b,a)\), mientras que para conjuntos \(\{a,b\}=\{b,a\}\).

Definición 1.15 (Producto cartesiano) Dados dos conjuntos \(A\) y \(B\), se llama producto cartesiano de \(A\) y \(B\), y se denota \(A\times B\), al conjunto de los pares ordenados

\[A \times B = \{ (a,b) \, : \, a \in A \mbox{ y } b \in B \}\]

De manera más general, si se tienen \(n\) conjuntos \(A_1, A_2, \ldots, A_n\), el producto cartesiano generalizado es

\[A_1 \times A_2 \times \ldots \times A_n = \{ (a_1, \ldots, a_n) \, :\, a_i \in A_i\ \forall i=1, \ldots n\}\]

Ejemplo 1.12 El producto cartesiano de los conjuntos \(A=\{a, b, c\}\) y \(B=\{1, 2\}\) es

\[ A\times B = \{(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)\} \]

Definición 1.16 (Relación binaria) Dados dos conjuntos \(A\) y \(B\), se dice que \(R\) es una relación binaria sobre \(A\) y \(B\) si es un subconjunto del producto cartesiano de \(A\) y \(B\), es decir, \[ R \subseteq A \times B. \]

Si \((a,b)\in R\) se escribe \(a R b\).

Si \(A\) y \(B\) son el mismo conjunto, se dice que \(R\) es una relación binaria homogénea.

Cuando un par ordenado pertenece a una relación, \((a,b)\in R\), también se suele escribir \(aRb\).

Dependiendo de las propiedades que cumpla una relación binaria homogénea tenemos los siguientes tipos de relaciones:

Reflexiva: \(\forall a \in A, (a,a) \in R\)
Irreflexiva: \(\forall a \in A, (a,a) \not\in R\).
Simétrica: \(\forall a, b \in A\), si \((a,b) \in R\), entonces \((b,a) \in R\).
Asimétrica: \(\forall a, b \in A\), si \((a,b) \in R\), entonces \((b,a) \not\in R\).
Antisimétrica: \(\forall a, b \in A\), si \((a,b) \in R\) y \((b,a) \in R\), entonces \(a = b\).
Transitiva: \(\forall a, b, c \in A\), si \((a,b) \in R\) y \((b,c) \in R\), entonces \((a,c) \in R\).
Total: \(\forall a, b \in A\), \((a,b) \in R\) o \((b,a) \in R\).

Definición 1.17 (Relación de equivalencia) Dado un conjunto \(A\) y una relación homogénea \(\sim \subseteq A \times A\), se dice que \(\sim\) es una relación de equivalencia si es que cumple que \(\sim\) es reflexiva, simétrica y transitiva, es decir, si cumple las propiedades

Reflexiva: \(\forall a \in A, a \sim a\).
Simétrica: \(\forall a, b \in A\), si \(a\sim b\) entonces \(b\sim a\).
Transitiva: \(\forall a, b, c \in A\), si \(a\sim b\) y \(b\sim c\), entonces \(a\sim c\).

Ejemplo 1.13 Ya hemos visto que la relación de igualdad matemática entre los elementos de un conjunto es una relación de equivalencia.

Definición 1.18 (Relación de orden) Dado un conjunto \(A\) y una relación homogénea \(\preceq \subseteq A \times A\), se dice que \(\preceq\) es una relación de orden, si es una relación reflexiva, antisimétrica y transitiva, es decir, si cumple las propiedades

Reflexiva: \(\forall a \in A, a \preceq a\).
Antisimétrica: \(\forall a, b \in A\), si \(a\preceq b\) y \(b\preceq a\), entonces \(a = b\).
Transitiva: \(\forall a, b, c \in A\), si \(a\preceq b\) y \(b\preceq c\), entonces \(a\preceq c\).

Definición 1.19 (Relación de orden parcial) Dado un conjunto \(A\) y una relación homogénea \(\preceq \subseteq A \times A\), se dice que \(\preceq\) es una relación de orden parcial, si es una relación de orden y al menos dos elementos de \(A\) están relacionados mediante \(\preceq\), es decir,

\[\exists x, y\in A,\ x\preceq y \mbox{ o } y\preceq x.\]

Al conjunto \(A\) con la relación de orden parcial \(\preceq\) se le llama conjunto parcialmente ordenado, y se denota \((A,\preceq)\).

Ejemplo 1.14 El conjunto potencia de un conjunto \(A\) con la relación de inclusión es un conjunto parcialmente ordenado \((\mathcal{P}(A),\subseteq)\).

Definición 1.20 (Relación de orden total) Dado un conjunto \(A\) y una relación homogénea \(\preceq \subseteq A \times A\), se dice que \(\preceq\) es una relación de orden total, si es una relación de orden y todos los elementos de \(A\) se relacionan entre sí mediante \(\preceq\), es decir,

\[\forall x, y\in A,\ x\preceq y \mbox{ o } y \preceq x.\]

Al conjunto \(A\) con la relación de orden total \(\preceq\) se le llama conjunto totalmente ordenado, y se denota \((A,\preceq)\).

Ejemplo 1.15 La relación de orden de los números naturales \((\mathbb{N},\leq)\) es un orden totalmente ordenado. Sin embargo, la relación de inclusión en el conjunto potencia de un conjunto \(A\) (\(\mathcal{P}(A),\subseteq\)) no es un orden totalmente ordenado, ya que dados dos elementos \(a\neq b\) de \(A\), se cumple que \(\{a\}\subsetneq \{b\}\) y \(\{b\}\subsetneq \{a\}\).

1.4 Cotas y extremos

Definición 1.21 (Cota superior) Dado un subconjunto con una relación de orden parcial \((A,\preceq)\) y un subconjunto \(B\subseteq A\), se dice que un elemento \(c\in A\) es una cota superior de \(B\), si todos los elementos de \(B\) son menores o iguales a \(c\) según la relación de orden, es decir,

\[\forall x \in B, x\preceq c.\]

El conjunto de todas las cotas superiores de \(B\) se denota \(\operatorname{CS}(B)\).

Ejemplo 1.16 Para el conjunto \(B=\{3, 4, 5\}\subseteq \mathbb{N}\), \(5\) es una cota superior. El conjunto de todas sus cotas superiores es \(\operatorname{CS}(B)=\{x\in \mathbb{N}:x\geq 5\}\).

Para el intervalo \([0,1)\subseteq \mathbb{R}\), cualquier número real \(x\geq 1\) es una cota superior, por lo que \(\operatorname{CS}([0,1)) = \{x\in \mathbb{R}:x\geq 1\}\).

Definición 1.22 (Cota inferior) Dado un subconjunto con una relación de orden parcial \((A,\preceq)\) y un subconjunto \(B\subseteq A\), se dice que un elemento \(c\in A\) es una cota inferior de \(B\), si todos los elementos de \(B\) son mayores o iguales a \(c\) según la relación de orden, es decir,

\[\forall x \in B, c\preceq x.\]

El conjunto de todas las cotas inferiores de \(B\) se denota \(\operatorname{CI}(B)\).

Ejemplo 1.17 El conjunto de las cotas inferiores de \(B=\{3, 4, 5\}\subseteq \mathbb{N}\) es \(\operatorname{CI}(B)=\{1, 2, 3\}\).

El conjunto de las cotas inferiores de \([0,1)\subseteq \mathbb{R}\) es \(\operatorname{CI}([0,1)) = \{x\in \mathbb{R}:x\leq 0\}\).

Definición 1.23 (Máximo) Dado un conjunto con una relación de orden parcial \((A,\preceq)\), se dice que un elemento \(m\in A\) es un máximo de \(A\), y se denota \(\max(A)\), si cualquier otro elemento de \(A\) es menor o igual que él según la relación de orden, es decir,

\[\forall x \in A, x\preceq m.\]

Ejemplo 1.18 El máximo de \(B=\{3, 4, 5\}\subseteq \mathbb{N}\), es \(5\).

El intervalo \([0,1)\subseteq \mathbb{R}\) no tiene máximo.

Definición 1.24 (Mínimo) Dado un conjunto con una relación de orden parcial \((A,\preceq)\), se dice que un elemento \(m\in A\) es un mínimo de \(A\), y se denota \(\min(A)\), si y cualquier otro elemento de \(A\) es mayor o igual que él según la relación de orden, es decir,

\[\forall x \in A, m\preceq x.\]

Ejemplo 1.19 El mínimo de \(B=\{3, 4, 5\}\subseteq \mathbb{N}\), es \(3\).

El mínimo del intervalo \([0,1)\subseteq \mathbb{R}\) es \(0\).

Teorema 1.1 (Unicidad de los extremos) Dado un conjunto con una relación de orden parcial \((A,\preceq)\), si existe el máximo de \(A\) entonces es único. Lo mismo es cierto para el mínimo.

Demostración

Prueba. Supongamos que \(A\) tiene dos máximos \(m\) y \(n\). Entonces, por la definición de máximo, \(x\preceq m\) \(\forall x\in A\), y en particular \(n\preceq m\). Del mismo modo, \(x\preceq n\) \(\forall x\in A\), y en particular \(m\preceq n\), pero como \(\preceq\) es una relación de orden, se deduce que \(m=n\).

Definición 1.25 (Supremo) Dado un subconjunto con una relación de orden parcial \((A,\preceq)\) y un subconjunto \(B\subseteq A\), se llama supremo de \(B\), y se denota \(\sup(B)\), a la menor de las cotas superiores de \(B\).

Ejemplo 1.20 El supremo del conjunto \(B=\{3, 4, 5\}\subseteq \mathbb{N}\), es \(5\) ya que es el mínimo del conjunto de sus cotas superiores \(\operatorname{CS}(B)=\{x\in \mathbb{N}:x\geq 5\}\).

El supremo del intervalo \([0,1)\subseteq \mathbb{R}\) es \(1\) ya que es el mínimo del conjunto de sus cotas superiores \(\operatorname{CS}([0,1)) = \{x\in \mathbb{R}:x\geq 1\}\).

Definición 1.26 (Ínfimo) Dado un subconjunto con una relación de orden parcial \((A,\preceq)\) y un subconjunto \(B\subseteq A\), se llama ínfimo de \(B\), y se denota \(\inf(B)\), a la mayor de las cotas inferiores de \(B\).

Ejemplo 1.21 El ínfimo del conjunto \(B=\{3, 4, 5\}\subseteq \mathbb{N}\), es \(3\) ya que es el máximo del conjunto de sus cotas inferiores \(\operatorname{CI}(B)=\{1, 2, 3\}\).

El ínfimo del intervalo \([0,1)\subseteq \mathbb{R}\) es \(0\) ya que es el máximo del conjunto de sus cotas inferiores \(\operatorname{CI}([0,1)) = \{x\in \mathbb{R}:x\leq 0\}\).

Advertencia

Obsérvese que un conjunto puede no tener cotas superiores o inferiores y, por tanto, no tener supremo o ínfimo.

Ejemplo 1.22 El conjunto \(B=\{x\in\mathbb{Z}: x \mbox{ es par}\}\), no tiene cotas superiores, ni inferiores, y por tanto tampoco tiene máximo, mínimo, supremo e ínfimo.

1.5 Funciones

El concepto de función es uno de los más importantes en el Análisis Matemático, ya que muchos de los fenómenos naturales en los que una magnitud depende de otra se modelizan mediante funciones.

Definición 1.27 (Función) Se dice que una relación binaria \(f \subseteq A \times B\), con \(A\) y \(B\) conjuntos no vacíos, es una función parcial o aplicación parcial, y se denota \(f:A\rightarrow B\), si \(f\) no contiene dos pares ordenados distintos con la misma primera componente, es decir,

\[ \forall a \in A, \forall b_1, b_2 \in B, \mbox{ si } (a,b_1) \in f \mbox{ y } (a,b_2) \in f, \mbox{ entonces } b_1 = b_2. \]

Si además, la relación es total en \(A\), es decir, todos los elementos de \(A\) aparecen en la relación, se dice que \(f\) es una función total o simplemente función.

De manera más informal podemos decir que una función es una correspondencia entre los elementos de dos conjuntos \(A\) y \(B\) que asocia a cada elemento de \(A\) un elemento, y solo uno, de \(B\).

Es habitual representar los pares de una función con la notación \(y=f(x)\) donde \(x\) es la primera componente del par e \(y\) la segunda.

Ejemplo 1.23 La relación binaria \(f=\{(1,d), (2,c), (3,a), (4,c)\}\) es una función, pero la relación \(g=\{(1,d), (2,b), (3,a), (3,c)\}\) no lo es porque existen dos pares cuya primera componente es \(3\).

Del mismo modo la función raíz cuadrada \(y=f(x)=\sqrt{x}\) no es una función en el conjunto de los números reales, ya que, por ejemplo \(\sqrt{1}=\pm 1\).

Definición 1.28 (Dominio) Dada una función \(f:A\rightarrow B\), se llama dominio de \(f\), y se denota \(\operatorname{Dom}(f)\) al conjunto de las primeras componentes de los pares de \(f\), es decir,

\[\operatorname{Dom}(f) = \{a\in A: \exists b\in B, (a,b)\in f\}\]

Definición 1.29 (Imagen) Dada una función \(f:A\rightarrow B\), se llama imagen de \(f\), y se denota \(\operatorname{Im}(f)\) al conjunto de las segundas componentes de los pares de \(f\), es decir,

\[\operatorname{Im}(f) = \{b\in B: \exists a\in A, (a,b)\in f\}\]

Definición 1.30 (Función inyectiva) Dada una función \(f:A\rightarrow B\), se dice que \(f\) es inyectiva si no existen dos elementos de \(A\) con la misma imagen, es decir,

\[\forall a_1, a_2 \in A, \mbox{ si } f(a_1) = f(a_2), \mbox{ entonces } a_1 = a_2.\]

Definición 1.31 (Función sobreyectiva) Dada una función \(f:A\rightarrow B\), se dice que \(f\) es sobreyectiva si todo elemento de \(B\) tiene una preimagen (está relacionado con algún elemento de \(A\) mediante \(f\)), es decir,

\[\forall b \in B, \exists a\in A, f(a) = b.\]

Definición 1.32 (Función biyectiva) Dada una función \(f:A\rightarrow B\), se dice que \(f\) es biyectiva, si \(f\) es, a la vez, inyectiva y sobreyectiva.

Definición 1.33 (Función identidad) Dado un conjunto \(A\), se llama función identidad de \(A\), y se denota \(\operatorname{id}_A:A\rightarrow A\), a la función que empareja cada elemento de \(A\) consigo mismo, es decir,

\[\operatorname{id}_A (a) = a, \forall a\in A.\]

Definición 1.34 (Función inversa) Dada una función \(f:A\rightarrow B\), se llama función inversa de \(f\), y se denota \(f^{-1}:B\rightarrow A\), a la función que resulta de revertir el orden de los pares de \(f\), es decir,

\[f^{-1} = \{ (b,a) : (a,b) \in f \}.\]

Obsérvese que para que exista la función inversa de \(f\), \(f\) debe ser inyectiva.

En muchas ocasiones, el valor de salida de una función se puede utilizar como la entrada de otra función, concatenando la aplicación de las dos funciones.

Definición 1.35 (Composición de funciones) Dadas dos funciones \(f:A\rightarrow B\) y \(g:C\rightarrow D\), tales que \(\operatorname{Im}(f)\subseteq \operatorname{Dom}(g)\), se llama composición de \(f\) con \(g\), y se denota \(g\circ f:A\rightarrow D\), a la funcion que a cada elemento del dominio de \(A\) le asocia el elemento que resulta de aplicar \(g\) a la imagen de \(a\) mediante \(f\), es decir,

\[g\circ f(a) = g(f(a)), \forall a\in A.\]

Proposición 1.4 Dada una función \(f:A\rightarrow B\), si existe \(f^{-1}\), entonces \(f\circ f^{-1} = \operatorname{id}_A\) y \(f^{-1}\circ f = \operatorname{id}_B\).

Demostración

Prueba. Sea \(a\in\operatorname{Dom}(A)\), y supongamos que \(f(a)=b\). Entonces \(f^{-1}(b)=a\), de manera que

\[ f\circ f^{-1}(a) = f(f^{-1}(a)) = f(b) = a. \]

1.6 Cardinalidad de un conjunto

Definición 1.36 (Cardinal) Dado un conjunto \(A\), se llama cardinal de \(A\), y se denota \(|A|\), al número de elementos de \(A\).

De manera informal, se puede decir que el cardinal de un conjunto es su tamaño.

Ejemplo 1.24 El cardinal del conjunto \(A=\{a, b, c\}\) es \(|A|=3\).

Proposición 1.5 El cardinal del conjunto potencia de un conjunto \(A\) es \(|\mathcal{P}(A)| = 2^{|A|}\).

Demostración

Prueba. Se puede dar una prueba mediante coeficientes binomiales. Si \(A\) tiene \(n\) elementos, es decir, \(|\)A\(|=n\), el número de subconjuntos distintos con \(k\) elementos es igual al número combinatorio \[\binom{n}{k}=\frac{n!}{k!(n-k)!}.\]

Como un subconjunto de \(A\) puede tener desde \(0\) hasta \(n\) elementos, en total, el número de posibles subconjuntos de \(A\) será

\[|\mathcal{P}(A)|=\binom{n}{0}+\binom{n}{1}+\cdots + \binom{n}{n} = \sum_{k=0}^n \binom{n}{k},\]

y según el teorema del binomio de Newton se tiene que

\[\sum_{k=0}^n \binom{n}{k}=2^n = 2^{|A|}.\]

Definición 1.37 (Conjuntos equipotentes) Se dice que dos conjuntos \(A\) y \(B\) son equipotentes, y se denota \(A\approx B\), si tienen la misma cantidad de elementos, es decir, si \(|A| = |B|\).

Proposición 1.6 Dos conjuntos \(A\) y \(B\) son equipotentes si y solo si cada elemento de \(A\) puede emparejarse con uno de \(B\), de manera que todos los elementos de \(B\) sean pareja de uno de \(A\) y solo de uno, es decir, existe una aplicación biyectiva \(f:A\rightarrow B\).

Demostración

Prueba. Si \(A\) y \(B\) son equipotentes, es trivial construir una biyección entre ellos, ya que podemos construir una función que empareje cada elemento de \(A\) con un único elemento de \(B\) y cada elemento de \(B\) con un único elemento de \(A\).

Por otro lado, si existe una aplicación biyectiva \(f\) entre \(A\) y \(B\), la asociación entre elementos es uno a uno, es decir, para cada elemento de \(A\) está emparejado exactamente con un uno de \(B\), y cada elemento de \(B\) está emparejado exactamente con uno de \(A\), con lo que necesariamente \(A\) y \(B\) deben tener el mismo número de elementos.

Proposición 1.7 La relación de equipotencia es una relación de equivalencia, es decir, satisface las siguientes propiedades:

Reflexiva: \(A\approx A\) para todo conjunto \(A\).
Simétrica: Si \(A\approx B\), entonces \(B\approx A\), para cualesquiera conjuntos \(A\) y \(B\).
Transitiva: Si \(A\approx B\) y \(B\approx C\), entonces \(A\approx C\) para cualesquiera conjuntos \(A\), \(B\) y \(C\).

Demostración

Prueba. Veamos que la relación de equipotencia cumple las propiedades reflexiva, simétrica y transitiva.

Reflexiva: Es trivial ya que cualquier conjunto tiene el mismo número de elementos que él mismo, luego \(A\approx A\).

Simétrica: Si \(A\approx B\) entonces, por la proposición anterior, existe una una biyección \(f:A\longrightarrow B\). Pero entonces, la función inversa \(f^{-1}:B\longrightarrow A\) es también una biyección entre \(B\) y \(A\), por lo que \(B\approx A\).

Transitiva: Si \(A\approx B\) y \(B\approx C\), entonces, por la proposición anterior, existen dos biyecciones \(f:A\longrightarrow B\) y \(g:B\longrightarrow C\). Pero entonces, la función \(g\circ f:A\longrightarrow C\) es también biyectiva, por lo que \(A\approx C\).

De igual modo se puede definir una relación que capture la noción de que un conjunto es de menor tamaño que otro.

Definición 1.38 (Conjunto minuspotente) Dados dos conjuntos \(A\) y \(B\), se dice que \(A\) es minuspotente a \(B\), y se denota \(A\preceq B\), si el cardinal de \(A\) es menor o igual que el de \(B\), es decir, si \(|A| \leq |B|\).

Proposición 1.8 El conjunto \(A\) es minuspotente al conjunto \(B\) si y solo si existe una aplicación inyectiva \(f:A\rightarrow B\).

Demostración

Prueba. Supongamos que \(A\preceq B\), entonces podemos tomar un subconjunto \(C\subseteq B\) con el mismo cardinal que \(A\) y crear una biyección entre \(A\) y \(C\). Tomando esta misma aplicación entre \(A\) y \(B\), la aplicación será inyectiva.

Para probar el otro sentido de la implicación, supongamos que existe una aplicación inyectiva \(f:A\longrightarrow B\), eso significa que todos los elementos de \(A\) están emparejados con elementos de \(B\) distintos entre sí, por lo que \(B\) tiene al menos el mismo número de elementos que \(A\), y por tanto, \(A\preceq B\).

Proposición 1.9 La relación de minuspotencia es una relación de orden, es decir, satisface las siguientes propiedades:

Reflexiva: \(A\preceq A\) para todo conjunto \(A\).
Antisimétrica: Si \(A\preceq B\) y \(B\preceq A\), entonces \(A\approx B\), para cualesquiera conjuntos \(A\) y \(B\).
Transitiva: Si \(A\preceq B\) y \(B\preceq C\), entonces \(A\preceq C\) para cualesquiera conjuntos \(A\), \(B\) y \(C\).

Demostración

Prueba. Veamos que la relación de minuspotencia satisface las propiedades reflexiva, antisimétrica y transitiva.

Reflexiva: Es trivial, ya que \(|A|\leq |A|\) para cualquier conjunto \(A\), por lo que \(A\preceq A\).

Antisimétrica: Si \(A\preceq B\) y \(B\preceq A\), entonces \(|A|\leq |B|\) y \(|B|\leq |A|\), y como la relación \(\leq\) es una relación de orden en \(\mathbb{N}\), se deduce que \(|A|=|B|\), por lo que \(A\approx B\).

Transitiva: Si \(A\preceq B\) y \(B\preceq C\), entonces \(|A|\leq |B|\) y \(|B|\leq |C|\), y como la relación \(\leq\) es una relación de orden en \(\mathbb{N}\), se deduce que \(|A|\leq |C|\), por lo que \(A\preceq C\).

Definición 1.39 (Conjunto finito) Se dice que un conjunto \(A\) es finito si es que existe un \(n\in\mathbb{N}\) tal que \(|A| = |\{1,2,3,\ldots,n \}|\). Cuando esto ocurre, el cardinal de \(A\) es \(|A|=n\).

Definición 1.40 (Conjunto infinito) Se dice que un conjunto \(A\) es infinito si no es finito. En tal caso su cardinal se denota \(|A|=\infty\).

Advertencia

Hay que dejar claro que el símbolo \(\infty\) es una notación de conveniencia y no representa a ningún número.

Ejemplo 1.25 El conjunto \(A=\{a, b, c\}\) es finito ya que puede definirse una aplicación biyectiva \(f:A\rightarrow \{1, 2, 3\}\) con los pares \(\{(1,a),(2,b), (3,c)\}\), y por tanto, \(|A| = 3\).

Por otro lado, el conjunto de los números naturales \(\mathbb{N}\) es infinito, ya que no puede ponerse en correspondencia biyectiva con ningún conjunto \(\{1,2,\ldots,n\}\) para ningún \(n\in\mathbb{N}\), y por tanto, \(|\mathbb{N}|=\infty\).

Cabe preguntarse si dos conjuntos infinitos son siempre del mismo tamaño. Para responder a la pregunta basta con aplicar la Proposición 1.6.

Ejemplo 1.26 El conjunto de los números naturales pares \(P\) es infinito y también lo es el conjunto de los números naturales \(\mathbb{N}\). Además ambos son equipotentes pues se puede definir una aplicación biyectiva \(f(n) = 2n\) \(\forall n\in\mathbb{N}\), de manera que \(\mathbb{N}\approx P\).

Sin embargo, como se verá más adelante, el conjunto de los números naturales \(\mathbb{N}\) no es equipotente al conjunto de los números reales \(\mathbb{R}\), sino minuspotente. Por tanto, existen conjuntos infinitos de distintos tamaños. Para demostrarlo se necesita introducir un nuevo concepto.

Definición 1.41 (Conjunto numerable) Se dice que un conjunto \(A\) es numerable si tiene el mismo cardinal que el conjunto de los números naturales \(\mathbb{N}\).

Corolario 1.1 Un conjunto \(A\) es numerable si existe una aplicación biyectiva \(f:\mathbb{N}\rightarrow A\).

Demostración

Prueba. La prueba de este resultado es inmediata aplicando la Proposición 1.6.

En otras palabras, un conjunto es infinito numerable si tiene correspondencia uno a uno con el conjunto de los números naturales \(\mathbb{N}\), y por tanto, podemos enumerar sus elementos, es decir, hay un primer elemento, un segundo, etc.

Ejemplo 1.27 En el ejemplo anterior hemos visto que el conjunto de los números pares es equipotente al conjunto de los números naturales, y por consiguiente, es numerable.

Del mismo modo se puede probar que el conjunto de los números enteros \(\mathbb{Z}\) también es numerable, pues se puede definir una aplicación biyectiva \(f:\mathbb{N}\rightarrow \mathbb{Z}\) de la siguiente manera

\(f(n)= \begin{cases} (n-1)/2 &\mbox{si } n\in \mathbb{N} \mbox{ es impar},\\ -n/2 &\mbox{si } n\in \mathbb{N} \mbox{ es par}. \end{cases}\)

Sin embargo, existen conjuntos infinitos que no son numerables, como por ejemplo el conjunto de los números reales \(\mathbb{R}\).

David Hilbert, propuso una interesante paradoja para probar este hecho, conocida como la paradoja del hotel infinito

Georg Cantor dio una prueba formal de esto mediante el siguiente teorema.

Teorema 1.2 (Cantor) El conjunto potencia de cualquier conjunto \(A\) tiene un cardinal estrictamente mayor que el cardinal de \(A\), es decir, \(|A| < |\mathcal{P}(A)|\).

Demostración

Prueba. Basta con demostrar que no existe una aplicación \(f:A\rightarrow \mathcal{P}(A)\) sobreyectiva, y para ello basta con encontrar un subconjunto \(B\) de \(A\) que no sea la imagen mediante \(f\) de ningún elemento de \(A\).

Tomando el siguiente subconjunto de \(A\)

\[B = \{x\in A: x\not \in f(x)\},\]

es decir, el conjunto de los elementos de \(A\) que no están contenidos en el subconjunto de \(A\) que le corresponde mediante \(f\), se puede probar por reducción al absurdo que \(B\) no puede ser la imagen mediante \(f\) de ningún elemento de \(A\).

Supóngase que que existe \(a\in A\) tal que \(B=f(a)\). Como \(B\) es un subconjunto de \(A\), pueden darse dos casos:

Si \(a\in B\), entonces por la definición de \(B\) se tiene que \(a\not \in f(a)=B\), lo cual es contradictorio.
Si \(a\not\in B\), entonces por la definición de \(B\) se tiene que \(a\in f(a)=B\), que también es contradictorio.

Así pues, en ambos casos se llega a una contradicción y, por tanto, se concluye que no existe \(a = f(B)\), por lo que \(f\) no es sobreyectiva y \(|A|<|\mathcal{P}(A)|=2^{|A|}\).

Teorema 1.3 (Cardinalidad del continuo) El conjunto de los números reales \(\mathbb{R}\) tiene un cardinal igual al del conjunto potencia del conjunto de los números naturales \(\mathcal{P}(\mathbb{N})\), es decir, \(|\mathbb{R}|=2^{|\mathbb{N}|}\).

Demostración

Prueba. Daremos una demostración partiendo del hecho de que cada número real tiene una expansión decimal infinita de la forma \(e.d\) donde \(e\) es la parte entera y \(d\) la decimal infinita (por ejemplo, \(3/2\) se puede representar por la expansión decimal infinita \(1.5000\ldots\)).

El número de dígitos en la parte decimal es numerable ya que pueden ponerse fácilmente en correspondencia biyectiva con \(\mathbb{N}\) y, por tanto, cualquier número real tendrá \(|\mathbb{N}|\) dígitos en su parte decimal, lo que nos da, al ser nuestro sistema de numeración en base 10, un total de \(10^{|\mathbb{N}|}\) posibles combinaciones en la parte decimal.

En cuanto a la parte entera, ya se ha visto que el conjunto de los números enteros es equipotente al de los números naturales, por lo que \(|\mathbb{Z}|=|\mathbb{N}|\).

Así pues, el número total de expansiones decimales infinitas es \(|\mathbb{N}|10^{|\mathbb{N}|}\), y como todo número real tienen una expansión decimal infinita, se tiene

\[|\mathbb{R}| \leq |\mathbb{N}|10^{|\mathbb{N}|}.\]

Por otro lado, aplicando el Teorema 1.2, \(|\mathbb{N}|\leq 2^{|\mathbb{N}|}\), por lo que finalmente se tiene

\(|\mathbb{R}| \leq |\mathbb{N}|10^{|\mathbb{N}|}\leq 2^{|\mathbb{N}|}10^{|\mathbb{N}|} \leq 2^{|\mathbb{N}|}(2^4)^{|\mathbb{N}|}= 2^{|\mathbb{N}|+4|\mathbb{N}|} = 2^{|\mathbb{N}|}\), ya que por aritmética de las cardinalidades se tiene que \(|\mathbb{N}|+4|\mathbb{N}|=|\mathbb{N}|\).

Para probar el otro sentido de la desigualdad, basta tomar el conjunto de las fracciones decimales de la forma \(0.d_1d_2d_3\ldots\) donde \(d_i\in\{0,1\}\) (por ejemplo \(0.101000\ldots\)) que claramente es un subconjunto de \(\mathbb{R}\). Puesto que cada número de este conjunto tiene infinitos dígitos decimales, de nuevo, se puede poner en correspondencia biyectiva cada dígito con un número natural, y como para cada posición hay dos posibles dígitos (\(0\) y \(1\)), el número total de números en este conjunto es \(2^{|\mathbb{N}|}\), por lo que se tiene que \(2^{|\mathbb{N}|}\leq |\mathbb{R}|\).

Así pues, como \(|\mathbb{R}| \leq 2^{|\mathbb{N}|}\) y \(2^{|\mathbb{N}|}\leq |\mathbb{R}|\), se concluye que \(|\mathbb{R}| = 2^{|\mathbb{N}|}\).

Tomando iterativamente el conjunto potencia de un conjunto infinito y aplicando el teorema de Cantor, obtenemos una jerarquía infinita de cardinales infinitos, cada uno estrictamente mayor que el anterior.