4 Sucesiones de números reales
\[ \newcommand{\mathbb{N}}{\mathbb{N}} \newcommand{\mathbb{Z}}{\mathbb{Z}} \newcommand{\mathbb{Q}}{\mathbb{Q}} \newcommand{\mathbb{R}}{\mathbb{R}} \newcommand{\mathbb{C}}{\mathbb{C}} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\Ext}{Ext} \DeclareMathOperator{\Fr}{Fr} \DeclareMathOperator{\Adh}{Adh} \DeclareMathOperator{\Ac}{Ac} \DeclareMathOperator{\sen}{sen} \]
Las sucesiones de números reales son claves para comprender el concepto de límite que es fundamental en el Análisis Matemático. En este capítulo se presenta el concepto de sucesión de números reales, el concepto de límite y algunos resultados importantes sobre la convergencia de sucesiones.
4.1 Concepto de sucesión
Definición 4.1 (Sucesión de números reales) Una sucesión de números reales es una aplicación \(a:\mathbb{N}\to \mathbb{R}\) que asigna a cada número natural \(n\) un número real \(a_n\), conocido como término de la sucesión.
Utilizaremos la notación \((a_n)_{n=1}^\infty\), donde \(a_n=a(n)\) con \(n\in\mathbb{N}\), o simplemente \(a_n\), para referirnos a la sucesión definida por la aplicación \(a\).
De manera informal, se puede decir que una sucesión es una lista ordenada de números reales.
Ejemplo 4.1 La sucesión \(\left(\frac{1}{n}\right)_{n=1}^\infty\) está formada por los términos \(\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\).
No hay que confundir los términos de una sucesión \((a_n)_{n=1}^\infty\), que tienen orden, con el conjunto de los valores de la sucesión \(\{a_n:n\in\mathbb{N}\}\) que no tiene orden.
Ejemplo 4.2 La sucesión \(\left((-1)^n\right)_{n=1}^\infty\) está formada por los términos \(-1,1,-1,1,\ldots\), mientras que \(\{a_n:n\in\mathbb{N}\}=\{-1,1\}\).
Una sucesión de números reales puede definirse dando una fórmula para el término general, de manera que aplicando la fórmula para cada \(n\in\mathbb{N}\) se obtienen todos los términos de las sucesión, o bien de manera recursiva, dando el primer término de la sucesión y después dando una fórmula para construir el siguiente término de la sucesión en función del anterior o anteriores.
Ejemplo 4.3 La sucesión del ejemplo anterior también se puede definir recursivamente de la siguiente manera, \(a_1=-1\) y \(a_{n+1}=(-1)a_n\) \(\forall n\in\mathbb{N}\).
Otro ejemplo es la famosa sucesión de Fibonacci, que se define recursivamente como \(a_1=1\), \(a_2=1\) y \(a_{n+2}=a_n+a_{n+1}\) \(\forall n\in\mathbb{N}\).
Las operaciones aritméticas de los números reales se pueden extrapolar a las sucesiones aplicándolas término a término.
Definición 4.2 (Operaciones con sucesiones) Dadas dos sucesiones de números reales \((a_n)_{n=1}^\infty\) y \((b_n)_{n=1}^\infty\), se definen las siguientes operaciones:
Suma: \((a_n)_{n=1}^\infty + (b_n)_{n=1}^\infty = (a_n+b_n)_{n=1}^\infty\).
Diferencia: \((a_n)_{n=1}^\infty - (b_n)_{n=1}^\infty = (a_n-b_n)_{n=1}^\infty\).
Producto: \((a_n)_{n=1}^\infty (b_n)_{n=1}^\infty = (a_nb_n)_{n=1}^\infty\).
División: \(\dfrac{(a_n)_{n=1}^\infty}{(b_n)_{n=1}^\infty} = \left(\dfrac{a_n}{b_n}\right)_{n=1}^\infty\), siempre y cuando \(b_n\neq 0\) \(\forall n\in\mathbb{N}\).
Producto por escalar: \(c(a_n)_{n=1}^\infty = (ca_n)_{n=1}^\infty\).
Ejemplo 4.4 Dadas las sucesiones \((n)_{n=1}^\infty\) y \(((-1)^n)_{n=1}^\infty\) se tiene:
\[\begin{align*} (n)_{n=1}^\infty + ((-1)^n)_{n=1}^\infty &= (n + (-1)^n)_{n=1}^\infty = (0, 3, 2, 5, 4, \ldots)\\ (n)_{n=1}^\infty ((-1)^n)_{n=1}^\infty &= (n (-1)^n)_{n=1}^\infty = (-1, 2, -3, 4, -5, \ldots) \end{align*}\]
4.2 Límite de una sucesión
Definición 4.3 (Límite de una sucesión) Dada una sucesión \((a_n)_{n=1}^\infty\), se dice que un número \(a\in\mathbb{R}\) es el límite de la sucesión, si para cada \(\varepsilon>0\) existe un \(k\in\mathbb{N}\) a partir del cuál todos los términos de la sucesión caen en el entorno \((a-\varepsilon, a+\varepsilon)\), es decir, \(|a_n-a|<\varepsilon\) \(\forall n\geq k\).
Si \(a\) es el límite de la sucesión, se dice que la sucesión converge a \(a\), y se denota \(\lim_{n\to\infty}a_n = a\).
Si una sucesión tiene límite se dice que es convergente, y en caso contrario se dice que es divergente.
De manera informal podemos decir que una sucesión de números reales converge a un número \(a\), si para cualquier entorno suyo, a partir de un determinado término, todos los siguientes caen dentro del entorno, tal y como se muestra en la siguiente figura.
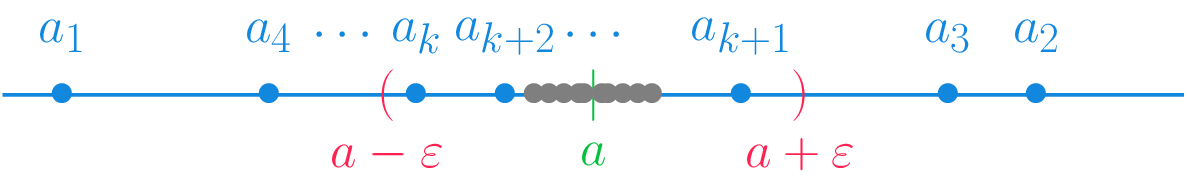
Esto es equivalente a decir que podemos encontrar términos de la sucesión tan cerca de \(a\) como queramos.
Ejemplo 4.5 La sucesión \((\frac{1}{n})_{n=1}^\infty\) es convergente y \(\lim_{n\to\infty}\frac{1}{n} = 0\), ya que para cualquier \(\varepsilon>0\), por la propiedad arquimediana, se tiene que existe un \(k\in\mathbb{N}\), tal que \(\frac{1}{k}<\varepsilon\), de manera que para cualquier \(n>k\), se tiene \(|\frac{1}{n}-0| = \frac{1}{n} <\frac{1}{k}<\varepsilon\).
Sin embargo, la sucesión \((n)_{n=1}^\infty\) diverge.
Teorema 4.1 Una sucesión de números reales puede tener a lo sumo un límite.
Prueba. Lo probaremos por reducción al absurdo. Supongamos que \((a_n)_{n=1}^\infty\) converge a \(a\) y \(b\) con \(a\neq b\). Entonces existe un \(\varepsilon>0\) tal que los entornos \((a-\varepsilon,a+\varepsilon)\) y \((b-\varepsilon,b+\varepsilon)\) son disjuntos. Ahora bien, por ser \(\lim_{n\to\infty}a_n = a\) existe un \(k_1\in\mathbb{N}\) tal que \(a_n\in(a-\varepsilon,a+\varepsilon)\) \(\forall n\geq k_1\), y por ser \(\lim_{n\to\infty}b_n = b\) existe un \(k_2\in\mathbb{N}\) tal que \(a_n\in(b-\varepsilon,b+\varepsilon)\) \(\forall n\geq k_2\). Basta tomar \(k=\max(k_1,k_2)\) para ver que \(a_k\) pertenece a ambos entornos, lo cual contradice que sean disjuntos. Por tanto, debe ser \(a=b\).
Definición 4.4 (Cola de una sucesión) Dada una sucesión de números reales \((a_n)_{n=1}^\infty\) y \(m\in\mathbb{N}\), se define la cola \(m\) de la sucesión, como la sucesión \((a_{m+n})_{n=1}^\infty = (a_{m+1}, a_{m+2},\ldots)\).
Proposición 4.1 Dada una sucesión de números reales \((a_n)_{n=1}^\infty\) y \(m\in\mathbb{N}\), la cola \((a_{m+n})_{n=1}^\infty\) converge si y solo si \((a_n)_{n=1}^\infty\) converge, y en tal caso, \(\lim_{n\to\infty}a_n=\lim_{n\to\infty}a_{m+n}\).
Prueba. Supongamos que la cola \((a_{m+n})_{n=1}^\infty\) converge a \(a\). Entonces, para cada \(\varepsilon>0\), existe un \(k_1\in\mathbb{N}\) tal que \(|a_{m+n}-a|<\varepsilon\) \(\forall n\geq k_1\). Tomando ahora \(k=k_1+m\in\mathbb{N}\) se tiene que para cualquier \(l\geq k\) \(|a_l-a| = |a_{l-m+m}-a| = |a_{m+n}-a| < \varepsilon\) siendo \(n=l-m\), ya que \(l\geq k_1+m\) y \(l-m\geq k_1\). Por tanto, \((a_n)_{n=1}^\infty\) converge a \(a\).
Para probar la otra implicación, supongamos ahora que \((a_n)_{n=1}^\infty\) converge a \(a\). Entonces, para cada \(\varepsilon>0\), existe un \(k\in\mathbb{N}\) tal que \(|a_n-a|<\varepsilon\) \(\forall n\geq k\). Pero como \(m\in\mathbb{N}\), si \(n\geq k\) también \(m+n\geq k\), con lo que \(|a_{m+n}-a|<\varepsilon\), y por consiguiente, \((a_{m+n})_{n=1}^\infty\) converge a \(a\).
Proposición 4.2 Sean \((a_n)_{n=1}^\infty\) y \((b_n)_{n=1}^\infty\) dos sucesiones de números reales tales que \((b_n)_{n=1}^\infty\) converge a 0. Si existe \(a, c\in\mathbb{R}\) con \(c>0\) tal que \(|a_n-a| < c|b_n|\) \(\forall n\in \mathbb{N}\), entonces \((a_n)_{n=1}^\infty\) converge a \(a\).
Prueba. Dado \(\varepsilon>0\), sea \(\varepsilon'=\frac{\varepsilon}{c}>0\). Como \((b_n)_{n=1}^\infty\) converge a 0, existe \(k\in\mathbb{N}\) tal que \(|b_n-0|=|b_n|<\varepsilon'\) \(\forall n\geq k\). Así pues, \(\forall n\geq k\) se tiene que \(|a_n-a|<c|b_n|<c\varepsilon'=c\frac{\varepsilon}{c}=\varepsilon\), por lo que \((a_n)_{n=1}^\infty\) converge a \(a\).
Ejemplo 4.6 Veamos que la sucesión \(\left(\frac{1}{2^n}\right)_{n=1}^\infty\) converge a 0. Para cualquier \(n\in\mathbb{N}\) se cumple que \(0<n<2^n\), de donde se deduce \(0<\frac{1}{2^n}<\frac{1}{n}\), lo que equivale a \(|\frac{1}{2^n}-0|<\frac{1}{n}\). Así pues, aplicando el teorema anterior y tomando \(c=1\), se concluye que \(\lim_{n\to\infty}\frac{1}{2^n}=0\).
Veamos ahora que \(\lim_{n\to\infty}n^{1/n}=1\). Aplicando el teorema del binomio, para cualquier \(n\in\mathbb{N}\), con \(n>1\), se tiene que
\[\begin{align*} \left(1+\sqrt{\frac{2}{n}}\right)^n &= 1^n + \binom{n}{1}1^{n-1}\sqrt{\frac{2}{n}} + \binom{n}{2}1^{n-2}\left(\sqrt{\frac{2}{n}}\right)^2 + \cdots \tag{1} \\ & > 1 + n\sqrt{\frac{2}{n}} + \frac{n(n-1)}{2!}\frac{2}{n} = 1 + \sqrt{\frac{2n^2}{n}} + n -1 \\ &= \sqrt{2n} + n > n \end{align*}\] (1) Los restantes términos del desarrollo del binomio son positivos.
Así pues,
\[ n^{1/n} < 1+\sqrt{\frac{2}{n}} \Leftrightarrow n^{1/n} - 1 < \sqrt{2}{\frac{1}{\sqrt{n}}} \Leftrightarrow |n^{1/n} - 1| < \sqrt{2}\frac{1}{\sqrt{n}}, \]
y como \(\sqrt{2}>0\) y \(\lim_{n\to\infty}\frac{1}{\sqrt{n}}=0\), por la proposición anterior teorema anterior se tiene que \(\lim_{n\to\infty} n^{1/n} = 1\).
Definición 4.5 (Sucesión acotada) Se dice que una sucesión de números reales \((a_n)_{n=1}^\infty\) está acotada si existe \(c>0\) tal que \(|a_n|\leq c\) \(\forall n\in\mathbb{N}\).
Teorema 4.2 Toda sucesión de números reales convergente está acotada.
Prueba. Sea \((a_n)_{n=1}^\infty\) una sucesión convergente a \(a\). Entonces, si tomamos \(\varepsilon=1\) existe un \(k\in\mathbb{N}\) tal que \(|a_n-a|<1\) \(\forall n\geq k\).
Por la desigualdad triangular (Proposición 2.4) se tiene que \(|a_n|=|a_n-a+a|\leq |a_n-a|+|a|<1 + |a|\), de donde se deduce que \(|a_n|<|a|+1\) \(\forall n\geq k\). Si se toma \(c=\max\{|a_1|,\ldots, |a_{k-1}|, |a|+1\}\) se tiene que si \(n<k\) entonces \(|a_n|\leq c\) y si \(n\geq k\) entonces \(|a_n| <|a|+1\leq c\), de modo que \(\forall n\in\mathbb{N}\) \(|a_n|\leq c\), por lo que \((a_n)_{n=1}^\infty\) está acotada.
Ejemplo 4.7 La sucesión \((n)_{n=1}^\infty\) diverge ya que no está acotada. Si estuviese acotada existiría un \(c>0\) tal que \(|n|\leq c\) \(\forall n\in\mathbb{N}\), lo que infringe la propiedad arquimediana.
El otro sentido de la implicación no se cumple, es decir, no toda sucesión acotada es convergente. Por ejemplo, la sucesión \(((-1)^n)_{n=1}^\infty\).
Proposición 4.3 Sean \((a_n)_{n=1}^\infty\) y \((b_n)_{n=1}^\infty\) dos sucesiones de números reales tales que \((a_n)_{n=1}^\infty\) converge a \(a\) y \((b_n)_{n=1}^\infty\) converge a \(b\). Entonces se cumple:
\((a_n)_{n=1}^\infty\) + \((b_n)_{n=1}^\infty\) converge a \(a+b\).
\((a_n)_{n=1}^\infty\) - \((b_n)_{n=1}^\infty\) converge a \(a-b\).
\((a_n)_{n=1}^\infty\) \((b_n)_{n=1}^\infty\) converge a \(ab\).
\(c(a_n)_{n=1}^\infty\) converge a \(ca\).
Si \(b_n\neq 0\) \(\forall n\in\mathbb{N}\) y \(b\neq 0\), \(\frac{(a_n)_{n=1}^\infty}{(b_n)_{n=1}^\infty}\) converge a \(\frac{a}{b}\).
Prueba. Veamos la prueba de cada apartado.
Dado \(\varepsilon>0\), sea \(\varepsilon'=\frac{\varepsilon}{2}>0\). Por ser \(\lim_{n\to\infty}a_n=a\) existe \(k_1\in\mathbb{N}\) tal que \(|a_n-a|<\varepsilon'=\frac{\varepsilon}{2}\) \(\forall n\geq k_1\), y por ser \(\lim_{n\to\infty}b_n=b\) existe \(k_2\in\mathbb{N}\) tal que \(|b_n-b|<\varepsilon'=\frac{\varepsilon}{2}\) \(\forall n\geq k_2\).
Tomando \(k=\max(\{k_1,k_2\})\), para \(n\geq k\), aplicando la desigualdad triangular, se tiene que
\[\begin{align*} |(a_n+b_n)-(a+b)| &= |(a_n-a)+(b_n-b)|\\ &\leq |a_n-a|+|b_n-b|\\ &<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon. \end{align*}\]
Por tanto, \(\lim_{n\to\infty}a_n+b_n = a+b\).
Se prueba de manera análoga.
Dado \(\varepsilon>0\), sea \(\varepsilon_1=\frac{\varepsilon}{2|a|}>0\). Por ser \(\lim_{n\to\infty}b_n=b\) existe \(k_1\in\mathbb{N}\) tal que \(|b_n-b|<\varepsilon_1=\frac{\varepsilon}{2}\) \(\forall n\geq k_1\). Y por el teorema anterior, como \((b_n)_{n=1}^\infty\) converge, está acotada, de modo que existe una cota \(c>0\) tal que \(|b_n|\leq c\) \(\forall n\in\mathbb{N}\).
Sea ahora \(\varepsilon_2=\frac{\varepsilon}{2c}>0\). Por ser \(\lim_{n\to\infty}a_n=a\) existe \(k_2\in\mathbb{N}\) tal que \(|a_n-a|<\varepsilon_2=\frac{\varepsilon}{2}\) \(\forall n\geq k_2\).
Tomando ahora \(k=\max(\{k_1,k_2\})\), para \(n\geq k\), aplicando la desigualdad triangular, se tiene que
\[\begin{align*} |(a_nb_n)-(ab)| &= |(a_nb_n-ab_n)+(ab_n-ab)|\\ &\leq |(a_nb_n-ab_n)|+|(ab_n-ab)|\\ &= |(a_n-a)b_n|+|a(b_n-b)| \\ &= |(a_n-a)||b_n|+|a||(b_n-b)|\\ &< |(a_n-a)|c+|a||(b_n-b)|\\ &<c\varepsilon_2+|a|\varepsilon_1=\frac{\varepsilon}{2c}c+|a|\frac{\varepsilon}{2|a|}\\ &= \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon. \end{align*}\]
Por tanto, \(\lim_{n\to\infty}a_nb_n = ab\).
Se prueba a partir del resultado anterior, tomando la sucesión constante \((c)_{n=1}^\infty\).
Se deja como ejercicio.
Ejemplo 4.8 Veamos que la sucesión \(\left(\frac{2n+1}{n+3}\right)_{n=1}^\infty\) converge a 2.
\[\begin{align*} \lim_{n\to\infty}\frac{2n+1}{n+3} &= \lim_{n\to\infty}\frac{2+\frac{1}{n}}{1+\frac{3}{n}} = \frac{\lim_{n\to\infty}2+\frac{1}{n}}{\lim_{n\to\infty}1+\frac{3}{n}} = \\ &=\frac{\lim_{n\to\infty} 2 + \lim_{n\to\infty}\frac{1}{n}}{\lim_{n\to\infty} 1 + \lim_{n\to\infty}\frac{3}{n}} = \frac{2+0}{1+0} = 2. \end{align*}\]
Teorema 4.3 (Compresión de sucesiones convergentes) Dadas tres sucesiones de números reales \((a_n)_{n=1}^\infty\), \((b_n)_{n=1}^\infty\) y \((c_n)_{n=1}^\infty\), tales que \(a_n\leq b_n\leq c_n\) \(\forall n\in\mathbb{N}\), si \((a_n)_{n=1}^\infty\) y \((c_n)_{n=1}^\infty\) convergen a \(a\), entonces \((b_n)_{n=1}^\infty\) converge a \(a\).
Prueba. Supongamos que \(\lim_{n\to\infty} a_n = \lim_{n\to\infty} c_n=a\) y sea \(\varepsilon>0\). Si tomamos \(\varepsilon_1=\frac{\varepsilon}{4}>0\), como \((c_n)_{n=1}^\infty\) converge a \(a\), existe \(k_1\in\mathbb{N}\) tal que \(|c_n-a|<\varepsilon_1\) \(\forall n\geq k_1\). Y si tomamos \(\varepsilon_2 = \frac{\varepsilon}{2}>0\), como \((a_n)_{n=1}^\infty\) converge a \(a\), existe \(k_2\in\mathbb{N}\) tal que \(|a_n-a|<\varepsilon_2\) \(\forall n\geq k_2\). Entonces, si se toma \(k=\max(k_1,k_2)\), se cumple que para cualquier \(n\geq k\),
\[\begin{align*} |b_n-a| &= |b_n-c_n+c_n-a| \\ &\leq |b_n-c_n|+|c_n-a| \tag{prop.2.4 (f)}\\ &= c_n-b_n+|c_n-a| \\ &\leq c_n-a_n+|c_n-a| \\ &= |c_n-a_n|+|c_n-a| \\ &= |c_n-a+a-a_n|+|c_n-a| \\ &\leq |c_n-a|+|a-a_n|+|c_n-a| \\ &= 2|c_n-a|+|a-a_n| \tag{prop.2.4 (f)}\\ &= 2|c_n-a|+|a_n-a| \tag{prop.2.4 (b)}\\ &< 2\varepsilon_1+\varepsilon_2 = 2\frac{\varepsilon}{4}+\frac{\varepsilon}{2}=\varepsilon. \end{align*}\]
Por tanto, \(\lim_{n\to\infty} b_n=a\).
Ejemplo 4.9 Veamos que la sucesión \(\left(\frac{2n}{n^2+1}\right)_{n=1}^\infty\) converge a 0. Para ello basta con ver que
\[ 0\leq \frac{2n}{n^2+1} \leq \frac{2n}{n^2}\leq \frac{2}{n}\ \forall n\in\mathbb{N} \]
y que \(\lim_{n\to\infty} \frac{2}{n}=\lim_{n\to\infty} 0 = 0\), de manera que aplicando el teorema anterior de compresión se tiene que \(\lim_{n\to\infty} \frac{2n}{n^2+1}=0\).
Veamos ahora que la sucesión \(\left(\frac{\operatorname{sen}(n)}{n}\right)_{n=1}^\infty\) también converge a 0. De nuevo basta con ver que, como \(-1\leq \operatorname {sen}(n)\leq 1\) \(\forall n\in\mathbb{N}\),
\[ \frac{-1}{n}\leq \frac{\operatorname{sen}(n)}{n} \leq \frac{1}{n}\ \forall n\in\mathbb{N} \]
y que \(\lim_{n\to\infty} \frac{-1}{n}=\lim_{n\to\infty} \frac{1}{n}= 0\), de manera que aplicando el teorema anterior de compresión se tiene que \(\lim_{n\to\infty} \frac{\operatorname{sen}(n)}{n}=0\).
Proposición 4.4 (Criterio del cociente) Si \((a_n)_{n=1}^\infty\) es una sucesión de números reales estrictamente positivos tal que la sucesión \(\left(\frac{a_{n+1}}{a_n}\right)_{n=1}^\infty\) converge a \(a<1\), entonces \((a_n)_{n=1}^\infty\) converge a 0.
Prueba. Sea \(b\) tal que \(a<b<1\) y tomemos \(\varepsilon=b-a>0\). Como \(\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=a\), existe un \(k\in\mathbb{N}\) tal que \(|\frac{a_{n+1}}{a_n}-a|\leq \varepsilon\) \(\forall n\geq k\), y por tanto, se tiene que para cualquier \(n\geq k\),
\[\begin{align*} \left|\frac{a_{n+1}}{a_n}-a\right|\leq \varepsilon &\Rightarrow -\varepsilon<\frac{a_{n+1}}{a_n}-a\leq \varepsilon\\ &\Rightarrow \frac{a_{n+1}}{a_n}\leq a+\varepsilon=a+b-a=b\\ &\Rightarrow a_{n+1}<ba_n. \end{align*}\]
Por consiguiente, si \(m\in\mathbb{N}\) se cumple que \(a_{k+m}<ba_{k+m-1}<b^2a_{k+m-2}<\cdots<b^ma_k\), de manera que \(0<a_{k+m}<b^ma_k\) \(\forall m\in\mathbb{N}\). Como \(b<1\), \(\lim_{m\to\infty}b^m=0\) y \(\lim_{m\to\infty}b^ma_k=0\), y por el teorema de compresión (Teorema 4.3) \(\lim_{m\to\infty}a_{k+m}=0\). Finalmente, como \((a_{k+m})_{m=1}^\infty\) es una cola de la sucesión \((a_n)_{n=1}^\infty\) se tiene que \(\lim_{n\to\infty}a_n=0\).
Ejemplo 4.10 Veamos que la sucesión \(\left(\frac{n}{2^n}\right)_{n=1}^\infty\) converge a 0.
\[\begin{align*} \lim_{n\to\infty}\frac{a_{n+1}}{a_n} &= \lim_{n\to\infty}\frac{\frac{n+1}{2^{n+1}}}{\frac{n}{2^n}} = \lim_{n\to\infty}\frac{1}{2}\frac{n+1}{n} \\ &= \lim_{n\to\infty} \frac{1}{2}\left(\frac{1}{n}+1\right) = \lim_{n\to\infty} \frac{1}{2}+\frac{1}{2n} \\ &= \lim_{n\to\infty} \frac{1}{2} + \lim_{n\to\infty} \frac{1}{2n} = \frac{1}{2}<1. \end{align*}\]
Así pues, por la proposición anterior, \(\lim_{n\to\infty}\frac{n}{2^n} = 0\).
4.3 Sucesiones monótonas
Veremos a continuación un tipo particular de sucesiones, cuyos términos siempre crecen o decrecen. Estas sucesiones son de especial importancia en aplicaciones del Análisis Matemático.
Definición 4.6 (Sucesión monónota) Dada una sucesión de números reales \((a_n)_{n=1}^\infty\):
- Se dice que es una sucesión creciente, si \(a_n\leq a_{n+1}\) \(\forall n\in\mathbb{N}\), y se dice que es estrictamente creciente si \(a_n< a_{n+1}\) \(\forall n\in\mathbb{N}\).
- Se dice que es una sucesión decreciente, si \(a_n\geq a_{n+1}\) \(\forall n\in\mathbb{N}\), y se dice que es estrictamente decreciente si \(a_n>a_{n+1}\) \(\forall n\in\mathbb{N}\).
- Se dice que es una sucesión monótona, si es creciente o decreciente.
Ejemplo 4.11 Las sucesiones \((2n)_{n=1}^\infty\) y \((n^2)_{n=1}^\infty\) son estrictamente crecientes y la sucesión \(\left(\frac{1}{n}\right)_{n=1}^\infty\) es estrictamente decreciente.
La sucesión \((a^n)_{n=1}^\infty\) es estrictamente creciente si \(a>1\) y estrictamente decreciente si \(0<a<1\). Si \(a=1\) la sucesión es, a la vez, creciente y decreciente, ya que en realidad es constante.
Sin embargo, la sucesión \(((-2)^n)_{n=1}^\infty\) no es monótona.
Teorema 4.4 (Convergencia de una sucesión monótona) Una sucesión de números reales monótona \((a_n)_{n=1}^\infty\) converge si y solo si está acotada. Además se cumple que:
- Si \((a_n)_{n=1}^\infty\) es una sucesión creciente y acotada, entonces \(\lim_{n\to\infty}a_n = \sup(\{a_n:n\in\mathbb{N}\})\).
- Si \((a_n)_{n=1}^\infty\) es una sucesión decreciente y acotada, entonces \(\lim_{n\to\infty}a_n = \inf(\{a_n:n\in\mathbb{N}\})\).
Prueba. Por el Teorema 4.2 ya se vio que toda sucesión convergente está acotada. Veamos ahora que si \((a_n)_{n=1}^\infty\) es una sucesión monótona acotada, entonces converge.
Sea \((a_n)_{n=1}^\infty\) una sucesión creciente y acotada, entonces el conjunto de los términos de la sucesión \(A=\{a_n:n\in\mathbb{N}\}\) no está vacío y está acotado, y por el axioma del supremo, existe \(s=\sup(A)\). Para ver que \((a_n)_{n=1}^\infty\) converge a \(s\), tomemos cualquier \(\varepsilon>0\). Como \(s\) es el supremo de \(A\), \(s-\varepsilon\) no es cota superior de \(A\) de manera que existe \(k\in\mathbb{N}\) tal que \(a_k>s-\varepsilon\). Si tomamos ahora cualquier \(n\geq k\), por ser la sucesión monótona, se tiene que \(a_k\leq a_n\), y al mismo tiempo \(a_n<s\) por ser \(s\) una cota superior de la sucesión. Por tanto, para cualquier \(n\geq k\) se cumple
\[ s-\varepsilon \leq a_k\leq a_n\leq s< s+\varepsilon \Rightarrow -\varepsilon < a_n-s <\varepsilon \Rightarrow |a_n-s|<\varepsilon, \]
lo que prueba que \(\lim_{n\to\infty}a_n = s\).
De forma similar se puede probar que si \((a_n)_{n=1}^\infty\) una sucesión decreciente y acotada, entonces \(\lim_{n\to\infty}a_n = \inf(\{a_n:n\in\mathbb{N}\})\).
Ejemplo 4.12 Veamos que la sucesión \(\left(\frac{1}{\sqrt{n}}\right)_{n=1}^\infty\) converge a 0. La sucesión es decreciente ya que para cualquier \(n\in\mathbb{N}\) se tiene que \(n<n+1 \Rightarrow \sqrt{n}< \sqrt{n+1} \Rightarrow \frac{1}{\sqrt{n}}> \frac{1}{\sqrt{n+1}}\). Como además está acotada inferiormente por el \(0\), se tiene que \(\lim_{n\to\infty}\frac{1}{\sqrt{n}} = \inf\left(\left\{\frac{1}{\sqrt{n}}: n\in\mathbb{N}\right\}\right)= 0\).
Ejemplo 4.13 Sea la sucesion definida recursivamente de la siguiente manera: \(a_1=1\) y \(a_{n+1}= \sqrt{2a_n}\). Veamos que converge a \(2\).
En primer lugar, veremos que es una sucesión creciente por inducción. Para \(n=1\) se tiene que \(a_1=1<\sqrt{2}=a_2\). Supongamos ahora que \(a_n<a_{n+1}\). Entonces, \(a_{n+2}=\sqrt{2a_{n+1}}>\sqrt{2a_n}=a_{n+1}\), de manera que la sucesión es creciente.
En segundo lugar, veremos, también por inducción, que \(a_n\leq 2\) \(\forall n\in\mathbb{N}\). Para \(n=1\) se tiene que \(a_1=1<2\). Supongamos ahora que \(a_n<2\). Entonces, \(a_{n+1}=\sqrt{2a_n}=\sqrt{2}\sqrt{a_n}<\sqrt{2}\sqrt{2}=2\). Luego, la sucesión está acotada, y por el teorema anterior, converge. Para calcular el límite, aprovechando la definición recursiva de la sucesión, se tiene
\[\begin{align*} a &=\lim_{n\to\infty}a_n = \lim_{n\to\infty} a_{n+1} = \lim_{n\to\infty} \sqrt{2a_n} = \lim_{n\to\infty}\sqrt{2}\sqrt{a_n}\\ &= \lim_{n\to\infty}\sqrt{2}\lim_{n\to\infty}\sqrt{a_n}=\sqrt{2}\sqrt{a}=\sqrt{2a}. \end{align*}\]
Así pues, se tiene que
\[ a=\sqrt{2a}\Rightarrow a^2=2a \Rightarrow a^2-2a=0 \Rightarrow a(a-2) = 0, \]
de donde se deduce, resolviendo la ecuación, que \(a=0\) o \(a=2\). Como \(a=0\) es imposible pues \(a_n\geq 1\) \(\forall n\in\mathbb{N}\), se concluye que \(a=2\), y por tanto, \(\lim_{n\to\infty}a_n = 2\).
Ejemplo 4.14 Veamos ahora que la sucesión \(\left(\left(1+\frac{1}{n}\right)^n\right)_{n=1}^\infty\) es convergente. Sea \(a_n=\left(1+\frac{1}{n}\right)^n\), entonces por el desarrollo del binomio, se tiene
\[\begin{align*} a_n &= \left(1+\frac{1}{n}\right)^n \\ &= \binom{n}{0}1^n\left(\frac{1}{n}\right)^0+\binom{n}{1}1^{n-1}\left(\frac{1}{n}\right)^1 + \binom{n}{2}1^{n-2}\left(\frac{1}{n}\right)^2 +\cdots + \binom{n}{n}1^0\left(\frac{1}{n}\right)^n \\ & = \binom{n}{0}1+\binom{n}{1}\frac{1}{n} + \binom{n}{2}\frac{1}{n^2} + \binom{n}{3}\frac{1}{n^3} +\cdots + \binom{n}{n}\frac{1}{n^n} \\ & = 1+n\frac{1}{n} + \frac{n(n-1)}{2!}\frac{1}{n^2} + \frac{n(n-1)(n-2)}{3!}\frac{1}{n^3} +\cdots + \frac{n!}{n!}\frac{1}{n^n} \\ &= 1 + 1 + \frac{1}{2!}\left(1-\frac{1}{n}\right) + \frac{1}{3!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) + \cdots + \frac{1}{n!}\left(1-\frac{1}{n}\right)\cdots \left(1-\frac{n-1}{n}\right). \end{align*}\]
y
\[\begin{align*} a_{n+1} &= \left(1+\frac{1}{n}\right)^{n+1} \\ &= 1 + 1 + \frac{1}{2!}\left(1-\frac{1}{n+1}\right) + \frac{1}{3!}\left(1-\frac{1}{n+1}\right)\left(1-\frac{2}{n+1}\right) + \cdots \\ &+ \frac{1}{n!}\left(1-\frac{1}{n+1}\right)\cdots \left(1-\frac{n-1}{n+1}\right) + \frac{1}{(n+1)!}\left(1-\frac{1}{n+1}\right)\cdots \left(1-\frac{n}{n+1}\right). \end{align*}\]
Como se puede observar, el desarrollo de \(a_n\) tiene \(n+1\) términos, mientras que el de \(a_{n+1}\) tiene \(n+2\) términos. Además, cada uno de los términos que aparece en \(a_n\) es menor o igual que el termino correspondiente de \(a_{n+1}\), de modo que se puede concluir que \(a_n<a_{n+1}\) \(\forall n\in\mathbb{N}\), y la sucesión es creciente.
Por otro lado, como se cumple que \(\left(1-\frac{k}{n}\right)<1\) \(\forall k=1,\ldots,n\), entonces
\[\begin{align*} a_n &= 1 + 1 + \frac{1}{2!}\left(1-\frac{1}{n}\right) + \frac{1}{3!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) + \cdots + \frac{1}{n!}\left(1-\frac{1}{n}\right)\cdots \left(1-\frac{n-1}{n}\right) \\ &< 1 + 1 + \frac{1}{2!} + \frac{1}{3!}+\cdots + \frac{1}{n!} \end{align*}\]
y como \(2^{n-1}\leq n!\) \(\forall n\in\mathbb{N}\), finalmente se tiene
\[ a_n<1+1+\frac{1}{2}+\frac{1}{2^2}+\cdots+\frac{1}{2^{n-1}} = 2+ \frac{\frac{1}{2^{n-1}}\frac{1}{2}-\frac{1}{2}}{\frac{1}{2}-1} = 2 +1 -\frac{1}{2^{n-1}} < 3. \]
Así pues, \((a_n)_{n=1}^\infty\) es creciente y está acotada, de manera que por el teorema anterior, es convergente, y como además \(2<a_n<3\) \(\forall n\in\mathbb{N}\), su límite es un número entre 2 y 3. A este número se le llama \(e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n\), que es un número irracional.
4.4 Subsucesiones
Definición 4.7 (Subsucesión) Se dice que una sucesión de números reales \((b_n)_{n=1}^\infty\) es una subsucesión de otra sucesión \((a_n)_{n=1}^\infty\), si existe una sucesión estrictamente creciente de números naturales \((r_n)_{n=1}^\infty\), tal que \(b_n=a_{r_n}\) \(\forall n\in\mathbb{N}\).
Ejemplo 4.15 La sucesión \((b_n)_{n=1}^\infty = \left(\frac{1}{2n}\right)_{n=1}^\infty\) es una subsucesión de la sucesión \((a_n)_{n=1}^\infty =\left(\frac{1}{n}\right)_{n=1}^\infty\), ya que tomando \((r_n)_{n=1}^\infty = 2n\), se cumple que \(b_n=a_{r_n}\) \(\forall n\in\mathbb{N}\).
Del mismo modo, las sucesiones \(\left(\frac{1}{2^n}\right)_{n=1}^\infty\) y \(\left(\frac{1}{n!}\right)_{n=1}^\infty\) también son subsucesiones de \(\left(\frac{1}{n}\right)_{n=1}^\infty\).
Teorema 4.5 (Convergencia de las subsucesiones) Si una sucesión de números reales converge a \(a\) entonces cualquier subsucesión suya converge también a \(a\).
Prueba. Sea \((a_{r_n})_{n=1}^\infty\) una subsucesión de \((a_n)_{n=1}^\infty\). Como \((a_n)_{n=1}^\infty\) converge a \(a\), dado cualquier \(\varepsilon>0\), existe \(k\in\mathbb{N}\) tal que \(|a_n-a|<\varepsilon\) \(\forall n\geq k\).
Como \((r_n)_{n=1}^\infty\) es estrictamente creciente, \(r_n\geq n\) \(\forall n\in\mathbb{N}\), de manera que si \(n\geq k\), entonces \(r_n\geq n\geq k\), y por tanto, \(|a_{r_n}-a|<\varepsilon\), por lo que \((a_{r_n})_{n=1}^\infty\) converge a \(a\).
Ejemplo 4.16 Veamos que la sucesión \((a^n)_{n=1}^\infty\) converge a \(0\) cuando \(0<a<1\).
La sucesión es decreciente ya que \(a_{n+1}=a^{n+1}=a^na<a^n=a_n\) \(\forall n\in\mathbb{N}\) al ser \(0<a<1\), y también está acotada ya que \(0<a^n<1\) \(\forall n\in\mathbb{N}\), de manera que por el teorema de la convergencia de una sucesión monótona, se tiene que \((a^n)_{n=1}^\infty\) converge a un número \(a\).
Para averiguar el límite, como cualquier subsucesión suya también converge a \(a\) por el teorema anterior, en particular \((a^{2n})_{n=1}^\infty\) converge a \(a\), por lo que se tiene
\[ a = \lim_{n\to\infty} a^n = \lim_{n\to\infty} a^{2n} = \lim_{n\to\infty} (a^n)^2 = a^2. \]
Así pues, \(a^2=a\), de manera que, resolviendo la ecuación, \(a=0\) o \(a=1\). Como \((a^n)_{n=1}^\infty\) es decreciente y \(0<a^n<1\) \(\forall n\in\mathbb{N}\), tiene que ser \(a=0\).
Del teorema anterior se deduce que si una sucesión tiene dos subsucesiones que convergen a distintos límites, o una subsucesión que diverge, entonces dicha sucesión diverge.
Ejemplo 4.17 La sucesión \(((-1)^n)_{n=1}^\infty\) diverge pues la subsucesión \(((-1)^{2n})_{n=1}^\infty\) converge a \(1\) y la subsucesión \(((-1)^{2n+1})_{n=1}^\infty\) converge a \(-1\).
Teorema 4.6 (Bolzano-Weierstrass) Toda sucesión de números reales acotada tiene al menos una subsucesión convergente.
Prueba. Sea \((a_n)_{n=1}^\infty\) una sucesión de números reales acotada. Entonces, \(A=\{a_n:n\in\mathbb{N}\}\) es un conjunto acotado.
Si \(A\) es finito, existe un \(c\in A\) y una subsucesión \((a_{r_n})_{n=1}^\infty\) tal que \(a_{r_n}=c\) \(\forall n\in\mathbb{N}\), que al ser una sucesión constante, converge a \(c\).
Si \(A\) es infinito, como está acotado, por el Teorema 3.3, existe un \(a\in\mathbb{R}\) que es punto de acumulación de \(A\). Entonces, para cada \(n\in\mathbb{N}\), el conjunto \(A_n=(a-\frac{1}{n},a+\frac{1}{n})\cap A\neq \emptyset\), y de hecho es infinito. Tomando como \(r_1\) el primer número natural tal que \(a_{r_1}\in A_n\), \(r_2\) el primer número natural tal que \(r_2>r_1\) y \(a_{r_2}\in A_2\), y así sucesivamente, se puede construir una sucesión de números naturales \((r_n)_{n=1}^\infty\) estrictamente creciente, de manera que \((a_{r_n})_{n=1}^\infty\) es una subsucesión de \((a_n)_{n=1}^\infty\). Además, como \(a_{r_n}\in A_n\), se tiene que \(|a_{r_n}-a|<\frac{1}{n}\) \(\forall n\in\mathbb{N}\), de manera que \((a_{r_n})_{n=1}^\infty\) converge a \(a\).
Teorema 4.7 Cualquier conjunto de número reales \(A\subseteq\mathbb{R}\) es cerrado si y solo si toda sucesión de números reales en \(A\) que converge, lo hace a un número de \(A\).
Prueba. Supongamos que \(A\) es un conjunto cerrado y sea \((a_n)_{n=1}^\infty\) una sucesión de números reales en \(A\) tal que \(\lim_{n\to\infty} a_n=a\). Veremos que \(a\in A\) por reducción al absurdo. Para ello, supongamos que \(a\not\in A\). Entonces \(a\in \overline{A}\). Como \(A\) es cerrado, \(\overline{A}\) es abierto, y entonces, existe \(\varepsilon>0\) tal que \((a-\varepsilon,a+\varepsilon)\subset \overline{A}\). Por otro lado, como \(\lim_{n\to\infty}a_n=a\), existe \(k\in\mathbb{N}\) tal que \(\forall n\geq k\) se tiene \(|a_n-a|<\varepsilon \Rightarrow a_n\in (a-\varepsilon,a+\varepsilon)\subset \overline{A}\), de manera que \(a_n\not\in A\) \(\forall n\geq k\), lo que contradice que \((a_n)_{n=1}^\infty\) sea una sucesión de números en \(A\). Por tanto, debe ser \(a\in A\).
Veamos ahora el otro sentido de la implicación. Supongamos que cualquier sucesión de números en \(A\) que converge, lo hace a un número de \(A\). Si \(A\) no es cerrado, entonces \(\overline{A}\) no es abierto, de manera que existe \(a\in\overline{A}\) tal que \((a-\varepsilon,a+\varepsilon)\cap A\neq\emptyset\) \(\forall \varepsilon>0\). En particular, para cada \(n\in\mathbb{N}\) se tiene que \((a-\frac{1}{n},a+\frac{1}{n})\cap A\neq \emptyset\), por lo que podemos tomar \(a_n\in (a-\frac{1}{n},a+\frac{1}{n})\cap A\) de manera que la sucesión \((a_n)_{n=1}^\infty\) es una sucesión en \(A\) y además \(|a_n-a|<\frac{1}{n}\) \(\forall n\in\mathbb{N}\), así que, \(\lim_{n\to\infty}a_n=a\not\in A\), lo que contradice la hipótesis de partida, por lo que \(A\) debe ser cerrado.
Corolario 4.1 Cualquier sucesión de números reales en un conjunto cerrado y acotado tiene una subsucesión convergente a un número del conjunto.
Prueba. Sea \(A\subset \mathbb{R}\) un conjunto cerrado y acotado, y sea \((a_n)_{n=1}^\infty\) una sucesión en \(A\). Como \(A\) está acotado, \((a_n)_{n=1}^\infty\) también lo está, y por el Teorema 4.6 tiene una subsucesión \((a_{r_n})_{n=1}^\infty\) convergente. Ahora bien, como \((a_{r_n})_{n=1}^\infty\) converge y está definida en \(A\) que es cerrado, por el teorema anterior, se concluye que \(\lim_{n\to\infty}a_{r_n}\in A\).
4.5 Sucesiones propiamente divergentes
Ya hemos visto que una sucesión que no converge es divergente, pero existen distintos motivos por los que una sucesión puede no converger. En esta sección estudiamos un tipo particular de sucesiones que divergen porque no paran de crecer o decrecer.
Definición 4.8 (Sucesiones propiamente divergentes) Se dice que una sucesión de números reales \((a_n)_{n=1}^\infty\) tiene a \(\infty\), y se denota \(\lim_{n\to\infty}a_n=\infty\), si para cualquier \(\varepsilon\in\mathbb{R}\) existe un \(k\in\mathbb{N}\) tal que \(a_n\geq\varepsilon\) \(\forall n\geq k\).
Del mismo modo, se dice que \((a_n)_{n=1}^\infty\) tiene a \(-\infty\), y se denota \(\lim_{n\to\infty}a_n=-\infty\), si para cualquier \(\varepsilon\in\mathbb{R}\) existe un \(k\in\mathbb{N}\) tal que \(a_n\leq \varepsilon\) \(\forall n\geq k\).
Y se dice que \((a_n)_{n=1}^\infty\) es propiamente divergente cuando \(\lim_{n\to\infty}a_n=\pm\infty\).
Ejemplo 4.18 La sucesión \((-n)_{n=1}^\infty\) tiende a \(-\infty\), ya que dado \(\varepsilon<0\), por la propiedad arquimediana, existe \(k\in\mathbb{N}\) tal que \(-\varepsilon<k\), de manera \(\varepsilon>-k\), y por tanto, \(\forall n\geq k\), \(-n\leq -k < \varepsilon\).
La sucesión \((n^2)_{n=1}^\infty\) tiende a \(\infty\), ya que dado \(\varepsilon>0\), por la propiedad arquimediana, existe \(k\in\mathbb{N}\) tal que \(\sqrt{\varepsilon}<k\), de manera que \(\forall n\geq k\), \(n^2\geq k^2>\varepsilon\).
Proposición 4.5 Una sucesión monótona de números reales es propiamente divergente si y solo si no está acotada. Además, si la sucesión es creciente entonces tiende a \(\infty\), y si es decreciente tiende a \(-\infty\).
Prueba. Sea \((a_n)_{n=1}^\infty\) una sucesión creciente y no acotada. Entonces dado \(\varepsilon>0\), como \(\varepsilon\) no es cota de la sucesión, existe \(k\in\mathbb{N}\) tal que \(a_k>\varepsilon\). Por tanto, \(\forall n\geq k\), como la sucesión es creciente, se tiene que \(a_n\geq a_k>\varepsilon\). Luego \(\lim_{n\to\infty}a_n=\infty\).
De forma análoga se prueba que si \((a_n)_{n=1}^\infty\) es decreciente y no acotada, entonces \(\lim_{n\to\infty}a_n=-\infty\).
Proposición 4.6 Sean \((a_n)_{n=1}^\infty\) y \((b_n)_{n=1}^\infty\) dos sucesiones de números reales tales que \(a_n\leq b_n\) \(\forall n\in\mathbb{N}\). Entonces, si \((a_n)_{n=1}^\infty\) tiende a \(\infty\), \((b_n)_{n=1}^\infty\) también tiende a \(\infty\), y si \((b_n)_{n=1}^\infty\) tiende a \(-\infty\), \((a_n)_{n=1}^\infty\) también tiende a \(-\infty\).
Prueba. Supongamos que \(\lim_{n\to\infty}a_n=\infty\). Dado \(\varepsilon>0\), como \((a_n)_{n=1}^\infty\) tiende a \(\infty\), existe un \(k\in\mathbb{N}\) tal que \(a_n>\varepsilon\) \(\forall n\geq k\), y por tanto también se cumple que \(b_n\geq a_n>\varepsilon\) \(\forall n\geq k\), de manera que \(\lim_{n\to\infty}b_n=\infty\).
De forma análoga se prueba que si \(\lim_{n\to\infty}b_n=-\infty\), entonces \(\lim_{n\to\infty}a_n=-\infty\).
Proposición 4.7 Sean \((a_n)_{n=1}^\infty\), \((b_n)_{n=1}^\infty\) y \((c_n)_{n=1}^\infty\) sucesiones de números reales tales que \(\lim_{n\to\infty}a_n=\infty\), \(\lim_{n\to\infty}b_n=\infty\) y \(\lim_{n\to\infty}c_n=-\infty\), entonces
- \(\lim_{n\to\infty}(a_n+b_n)=\infty\).
- \(\lim_{n\to\infty}(a_nb_n)=\infty\).
- \(\lim_{n\to\infty}(a_nc_n)=-\infty\).
- \(\lim_{n\to\infty}ka_n=\infty\) \(\forall k>0\) y \(\lim_{n\to\infty}ka_n=-\infty\) \(\forall k<0\).
- \(\lim_{n\to\infty}\frac{1}{a_n}=0\).
Prueba. Se deja como ejercicio.
Proposición 4.8 Sean \((a_n)_{n=1}^\infty\) y \((b_n)_{n=1}^\infty\) dos sucesiones de números reales estrictamente positivos tales que la sucesión \(\left(\frac{a_n}{b_n}\right)_{n=1}^\infty\) converge a \(l\neq 0\). Entonces, \((a_n)_{n=1}^\infty\) tiende a \(\infty\) si y solo si \((b_n)_{n=1}^\infty\) tiende a \(\infty\).
Prueba. Sea \(\varepsilon=\frac{l}{2}>0\) ya que \(l>0\) al ser las sucesiones estrictamente positivas. Como \(\lim_{n\to\infty} \frac{a_n}{b_n}=l\), existe \(k\in\mathbb{N}\) tal que \(\forall n\geq k\) se tiene
\[\begin{align*} |a_n-l|<\varepsilon=\frac{l}{2} &\Rightarrow \frac{-l}{2}<\frac{a_n}{b_n}-l<\frac{l}{2}\\ &\Rightarrow \frac{l}{2}<\frac{a_n}{b_n}< \frac{3l}{2}\\ &\Rightarrow \frac{l}{2}b_n<a_n<\frac{3l}{2}b_n. \end{align*}\]
Ahora, si \(\lim_{n\to\infty}a_n=\infty\), por el teorema anterior, se tiene que \(\lim_{n\to\infty}\frac{3l}{2}b_n=\infty\), y como \(\frac{3l}{2}>0\) se concluye que \(\lim_{n\to\infty}b_n=\infty\).
Del mismo modo, si \(\lim_{n\to\infty}b_n=\infty\) entonces \(\lim_{n\to\infty}\frac{l}{2}b_n=\infty\), y por el teorema anterior, se tiene que \(\lim_{n\to\infty}a_n=\infty\).
4.6 Sucesiones de Cauchy
En la última sección de este capítulo, se introducen un tipo particular de sucesiones convergente que son de especial importancia para la definición de los números reales.
Definición 4.9 (Sucesión de Cauchy) Se dice que una sucesión \((a_n)_{n=1}^\infty\) es una sucesión de Cauchy si para cualquier \(\varepsilon>0\) existe un \(k\in\mathbb{N}\) tal que \(|a_n-a_m|<\varepsilon\) \(\forall n,m\geq k\).
Teorema 4.8 (Criterio de convergencia de Cauchy) Una sucesión de números reales es convergente si y solo si es una sucesión de Cauchy.
Prueba. Sea \((a_n)_{n=1}^\infty\) una sucesión convergente a \(a\). Entonces, dado \(\varepsilon>0\), tomando \(\varepsilon'=\frac{\varepsilon}{2}>0\) existe \(k\in\mathbb{N}\) tal que \(|a_n-a|<\varepsilon'\) \(\forall n\geq k\).
Ahora, si se toma \(n,m\geq k\), se tiene, aplicando la desigualdad triangular,
\[ |a_n-a_m|=|(a_n-a)+(a-a_m)| \leq |a_n-a| + |a-a_m| < \varepsilon' +\varepsilon' = \varepsilon, \]
por lo que \((a_n)_{n=1}^\infty\) es una sucesión de Cauchy.
Veamos ahora al implicación en el otro sentido. Sea \((a_n)_{n=1}^\infty\) una sucesión de Cauchy. Entonces, dado \(\varepsilon=1\), existe \(k\in\mathbb{N}\) tal que \(|a_n-a_m|<1\) \(\forall n,m\geq k\). Así pues, si \(n\geq k\), se tiene, aplicando de nuevo la desigualdad triangular,
\[ |a_n| = |a_n-a_k+a_k| \leq |a_n-a_k|+|a_k|<1+|a_k|. \]
Si se toma \(c=\max(\{|a_1|, \ldots, |a_{k-1}|,1+|a_k|\})\) entonces \(c\) es una cota de \((a_n)_{n=1}^\infty\). Aplicando ahora el Teorema 4.6 existe una subsucesión convergente \((a_{r_n})_{n=1}^\infty\) de \((a_n)_{n=1}^\infty\).
Sea \(\lim_{n\to\infty}a_{r_n}=a\). Veamos que \((a_n)_{n=1}^\infty\) converge a \(a\). Dado \(\varepsilon>0\), sea \(\varepsilon'=\frac{\varepsilon}{2}>0\). Como \((a_n)_{n=1}^\infty\) es una sucesión de Cauchy, existe \(k_1\in\mathbb{N}\) tal que \(|a_n-a_m|<\varepsilon'\) \(\forall n,m\geq k_1\). Por otro lado, como \((a_{r_n})_{n=1}^\infty\) converge a \(a\), existe \(k_2\in\mathbb{N}\) tal que \(|a_{r_n}-a|<\varepsilon'\) \(\forall n\geq k_2\). Tomando \(k=\max(\{k_1,k_2\})\), para cualquier \(n\geq k\) se tiene, de nuevo por la desigualdad triangular,
\[ |a_n-a| = |a_n-a_{r_k}+a_{r_k}-a|\leq |a_n-a_{r_k}|+|a_{r_k}-a| < \varepsilon'+\varepsilon'=\varepsilon, \] pues \(r_k\geq k\geq k_1\). Por consiguiente, \((a_n)_{n=1}^\infty\) converge a \(a\).
Ejemplo 4.19 Veamos que la sucesión \(\left(\frac{1}{n}\right)_{n=1}^\infty\) es de Cauchy. Dado \(\varepsilon>0\), tomando \(\frac{2}{\varepsilon}>0\), por la propiedad arquimediana, existe \(k\in\mathbb{N}\) tal que \(\frac{2}{\varepsilon}<k\) y, por tanto, \(\frac{2}{k}<\varepsilon\). Ahora, para cualquier \(n,m\geq k\) se tiene
\[ \left|\frac{1}{n}-\frac{1}{m}\right| \leq \left|\frac{1}{n}\right| +\left|\frac{1}{m}\right| =\frac{1}{n}+\frac{1}{m} \leq \frac{1}{k}+\frac{1}{k}=\frac{2}{k}<\varepsilon. \]
Sin embargo, la sucesión \((n)_{n=1}^\infty\) no es de Cauchy, ya que, dado \(\varepsilon=1\), para cualquier \(k\in\mathbb{N}\), si tomamos \(n=k\geq k\) y \(m=k+2\geq k\), se tiene que \(|a_n-a_m|>|k-(k+2)|=2>1=\varepsilon\).
Las sucesiones de Cauchy juegan un papel clave en la construcción de cuerpos completos, en particular el cuerpo de los números Reales, ya que el hecho de que sus términos estén cada vez más cerca los unos de los otros, hace que aquellos cuerpos en los que cualquier sucesión de Cauchy converge a un elemento del cuerpo sean cuerpos sin huecos o completos.
Ejemplo 4.20 El cuerpo de los números racionales \(\mathbb{Q}\) no es completo ya que existen sucesiones de Cauchy de números racionales, como \(\left((1+\frac{1}{n})^n\right)_{n=1}^\infty\), que converge al número \(e\) que no es racional.
El conjunto de los números irracionales \(\mathbb{R}\setminus\mathbb{Q}\) tampoco es completo, pues existen sucesiones de Cauchy de números irracionales, como \((2^{1/(n+1)})_{n=1}^\infty\), que converge a \(1\) que no es irracional.
4.7 Sucesiones de funciones
De igual modo que hemos estudiado las sucesiones de números reales, en Análisis también se estudian sucesiones de funciones. Como se verá más adelante, en el capítulo de series, estas sucesiones juegan un papel fundamental en el estudio de funciones complicadas mediante aproximaciones de funciones simples.
Definición 4.10 Una sucesión de funciones reales o sucesion funcional es una aplicación \(f:\mathbb{N}\to \mathbb{R}^{\mathbb{R}}\) que asigna a cada número natural \(n\) una función \(f_n:\mathbb{R}\to\mathbb{R}\).
Utilizaremos la notación \(\left(f_n\right)_{n=1}^\infty\) para referirnos a la sucesión funcional definida por \(f\).
Ejemplo 4.21 Los primeros términos de la sucesión funcional \(\left(\frac{x^n}{1+x^n}\right)_{n=1}^\infty\) son las funciones \(\frac{x}{1+x}\), \(\frac{x^2}{1+x^2}\), \(\frac{x^3}{1+x^3}\), …
Definición 4.11 (Convergencia puntual) Dada una sucesión de funciones \(\left(f_n\right)_{n=1}^\infty\) y un número \(x\in\operatorname{Dom}(f_n)\) \(\forall n\in\mathbb{N}\), se dice que la sucesión converge puntualmente en \(x\), si la sucesión de números reales \((f_n(x))_{n=1}^\infty\) converge.
El conjunto \(\mathcal{C}\) de todos los puntos en los que la sucesión \(\left(f_n\right)_{n=1}^\infty\) converge puntualmente se llama dominio de convergencia puntual, y la función \(f:\mathcal{C}\to\mathbb{R}\) definida por
\[ f(x) = \lim_{n\to\infty}f_n(x) \]
se llama función límite puntual de la sucesión.
Es importante no confundir la sucesión de funciones \(\left(f_n\right)_{n=1}^\infty\) con la sucesión de números reales \(\left(f_n(x)\right)_{n=1}^\infty\) que se obtiene al evaluar cada función de la sucesión funcional en \(x\).
Definición 4.12 (Convergencia uniforme) Dada una sucesión funcional \(\left(f_n\right)_{n=1}^\infty\) con dominio de convergencia puntual \(\mathcal{C}\) y la función límite puntual \(f\), y un intervalo no vacío \(I\subseteq \mathcal{C}\), se dice que la sucesión converge uniformemente a \(f\) en \(I\), si para cualquier \(\varepsilon>0\) existe \(k\in\mathbb{N}\) tal que \(\sup\{|f_n(x)-f(x)|: x\in I\}\leq \varepsilon\) \(\forall n\geq k\).
