7  Derivadas de funciones

En la mayoría de los problemas reales, las magnitudes que intervienen están relacionadas mediante ecuaciones o funciones. Para construir estos modelos matemáticos resulta imprescindible entender cómo varían unas magnitudes con respecto a las otras. En este capítulo abordamos el concepto de derivada, que surge de estudiar cómo varía una función cuando cambia la variable de la que depende. El concepto de derivada, junto al de integral, son los dos pilares fundamentales del Análisis Matemático, sobre los que se sostienen la mayor parte de las aplicaciones en Ciencia e Ingeniería.

7.1 El concepto de derivada

7.1.1 Tasa de variación media

Definición 7.1 (Incremento) Dada una función \(y=f(x)\), se llama incremento de \(f\) en un intervalo \([a,b]\) a la diferencia entre el valor de \(f\) en cada uno de los extremos del intervalo, y se nota

\[\Delta y= f(b)-f(a).\]

Cuando \(f\) es la función identidad \(y=x\), se cumple que

\[\Delta x=\Delta y= f(b)-f(a)=b-a,\]

y por tanto, el incremento de \(x\) en un intervalo es la amplitud del intervalo. Esto nos permite escribir el intervalo \([a,b]\) como \([a,a+\Delta x]\).

Definición 7.2 (Tasa de variación media) Dada una función \(y=f(x)\), se llama tasa de variación media de \(f\) en el intervalo \([a,a+\Delta x]\), al cociente entre el incremento de \(y\) y el incremento de \(x\) en dicho intervalo, y se escribe

\[ \operatorname{TVM}(f,[a,a+\Delta x])=\frac{\Delta y}{\Delta x}=\frac{f(a+\Delta x)-f(a)}{\Delta x}. \]

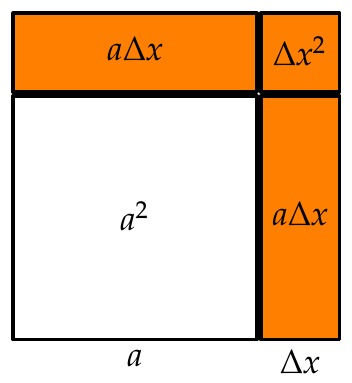
Ejemplo 7.1 Consideremos la función \(y=x^2\) que mide el área de un cuadrado de chapa metálica de lado \(x\).

Si en un determinado instante el lado del cuadrado es \(a\), y sometemos la chapa a un proceso de calentamiento que aumenta el lado del cuadrado una cantidad \(\Delta x\), ¿en cuánto se incrementará el área del cuadrado?

\[\begin{align*} \Delta y &= f(a+\Delta x)-f(a)=(a+\Delta x)^2-a^2=\\ &= a^2+2a\Delta x+\Delta x^2-a^2=2a\Delta x+\Delta x^2. \end{align*}\]

¿Cuál será la tasa de variación media del área en el intervalo \([a,a+\Delta x]\)?

\[\operatorname{TVM}f[a,a+\Delta x]=\frac{\Delta y}{\Delta x}=\frac{2a\Delta x+\Delta x^2}{\Delta x}=2a+\Delta x.\]

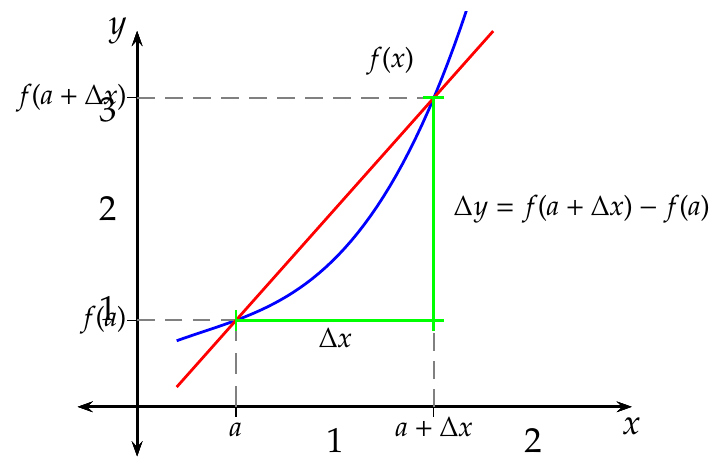
Variación que experimenta el area de un cuadrado al variar el lado

7.1.2 Interpretación geométrica de la tasa de variación media

La tasa de variación media de \(f\) en el intervalo \([a,a+\Delta x]\) es la pendiente de la recta secante a \(f\) en los puntos \((a,f(a))\) y \((a+\Delta x,f(a+\Delta x))\).

Gráfica de la recta secante a una función en dos puntos.

7.1.3 Tasa de variación instantánea

En muchas ocasiones, es interesante estudiar la tasa de variación que experimenta una función, no en intervalo, sino en un punto.

Conocer la tendencia de variación de una función en un instante puede ayudarnos a predecir valores en instantes próximos.

Definición 7.3 (Tasa de variación instantánea y derivada) Dada una función \(y=f(x)\), se llama tasa de variación instantánea de \(f\) en un punto \(a\), al límite de la tasa de variación media de \(f\) en el intervalo \([a,a+\Delta x]\), cuando \(\Delta x\) tiende a 0, y se denota

\[\begin{align*} \operatorname{TVI}(f,a) &= \lim_{\Delta x\rightarrow 0} \operatorname{TVM}(f,[a,a+\Delta x])=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x} = \\ &= \lim_{\Delta x\rightarrow 0}\frac{f(a+\Delta x)-f(a)}{\Delta x} \end{align*}\]

Cuando este límite existe, se dice que la función \(f\) es derivable en el punto \(a\), y al valor del mismo se le llama derivada de \(f\) en \(a\), y se nota como

\[ f'(a) \mbox{ o bien } \frac{df}{dx}(a) \]

Ejemplo 7.2 Consideremos de nuevo la función \(y=x^2\) que mide el área de un cuadrado de chapa metálica de lado \(x\).

Si en un determinado instante el lado del cuadrado es \(a\), y sometemos la chapa a un proceso de calentamiento que aumenta el lado del cuadrado, ¿cuál es la tasa de variación instantánea del área del cuadrado en dicho instante?

\[\begin{align*} \operatorname{TVI}(f(a)) &=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{f(a+\Delta x)-f(a)}{\Delta x} =\\ &=\lim_{\Delta x\rightarrow 0}\frac{2a\Delta x+\Delta x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0} 2a+\Delta x= 2a. \end{align*}\]

Así pues, \(f'(a)=2a\), lo que indica que la tendencia de crecimiento el área es del doble del valor del lado.

El signo de \(f'(a)\) indica la tendencia de crecimiento de \(f\) en el punto \(a\):

  • \(f'(a)>0\) indica que la tendencia es creciente.
  • \(f'(a)<0\) indica que la tendencia es decreciente.

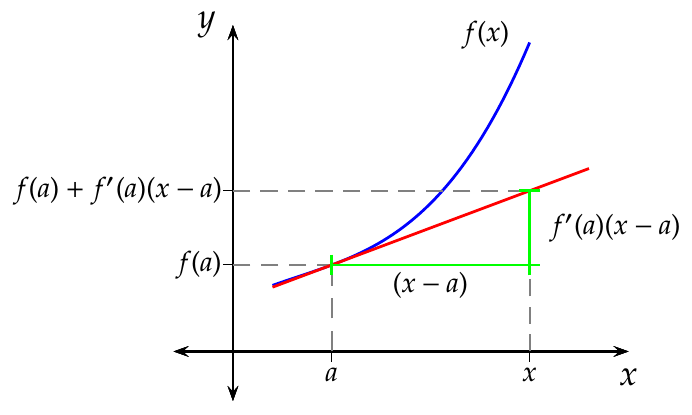
7.1.4 Interpretación geométrica de la tasa de variación instantánea

La tasa de variación instantánea de \(f\) en el punto \(a\) es la pendiente de la recta tangente a \(f\) en el punto \((a,f(a))\).

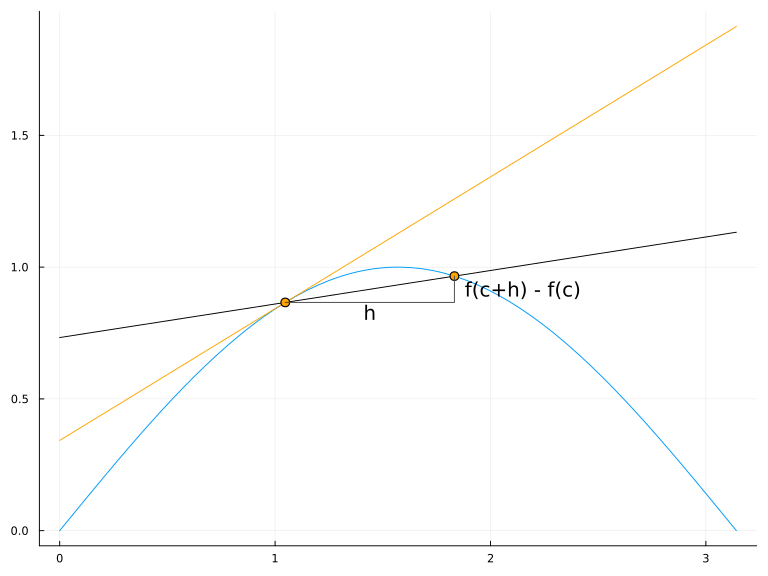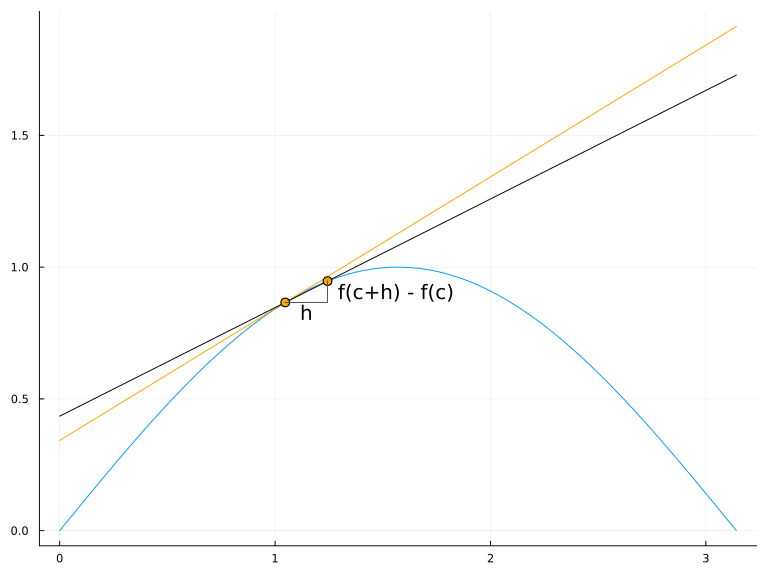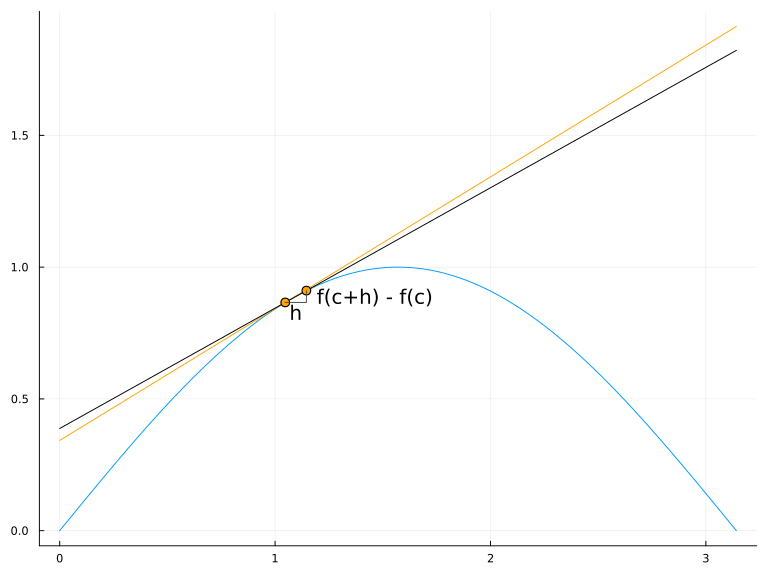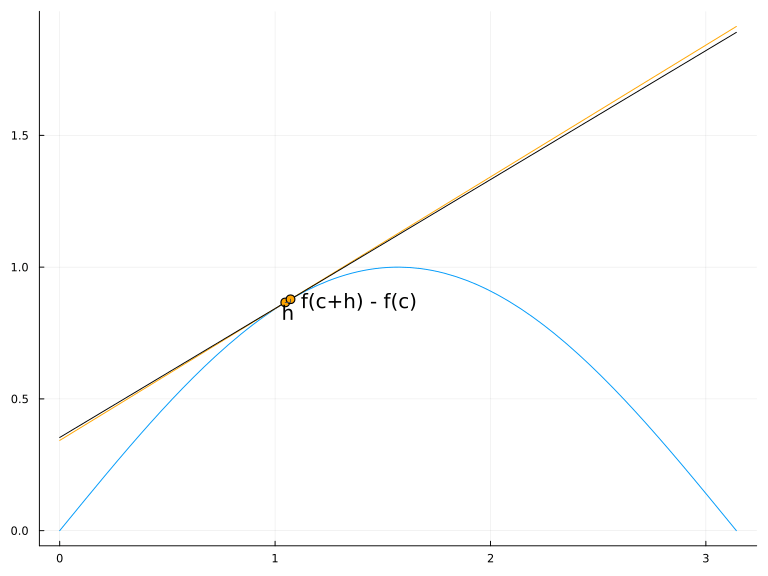
Gráfica de la recta tangente a una función en un punto.

Aproximación de la recta secante a la recta tangente en un punto.

7.2 Diferenciabilidad

Definición 7.4 (Función derivable) Dado un intervalo \(I\subseteq\mathbb{R}\), una función \(f:I\to\mathbb{R}\) y un punto \(a\in I\), se dice que \(f\) es diferenciable o derivable en \(a\), si existe el límite

\[ \lim_{x\to a}\frac{f(x)-f(a)}{x-a} \]

En tal caso, al valor del límite se le llama derivada de \(f\) en \(a\) y se denota \(f'(a)\).

Se dice que \(f\) es diferenciable en el intervalo \(I\), si \(f\) es diferenciable en todos los puntos de \(I\).

Nota

Si en la definición anterior llamamos \(h=x-a\), resulta

\[ f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}, \] que es otra definición equivalente de la derivada de \(f\) en \(a\).

Definición 7.5 (Función derivada) Dado un intervalo \(I\subseteq\mathbb{R}\) y una función \(f:I\to\mathbb{R}\), se define la función derivada de \(f\), y se denota \(f'\), a la función cuyo dominio es el conjunto de los puntos de \(I\) donde \(f\) es diferenciable y el valor de \(f'\) es el valor de la derivada en cada uno de esos puntos.

Nota

La notación \(f'(a)\) para la derivada de \(f\) se debe a Lagrange, pero también es común en Ciencias e Ingenierías utilizar la notación de \(\frac{df}{dx}\) debida a Leibniz. En esta última notación \(df\) y \(dx\) se conocen como diferenciales de \(f\) y \(x\), y representan variaciones infinitesimales de \(f\) y \(x\) respectivamente.

Ejemplo 7.3 Sea \(f(x)=Id(x)=x\) la función identidad. Entonces, para cualquier \(a\in\mathbb{R}\), se tiene que

\[ \lim_{x\to a}\frac{f(x)-f(a)}{x-a} = \lim_{x\to a}\frac{x-a}{x-a} = \lim_{x\to a}1 = 1. \]

Por tanto, \(Id(x)\) es diferenciable en todo \(\mathbb{R}\) y \(Id'(a)=a\).

Con la notación de Leibniz, el cálculo de la derivada es, si cabe, más sencillo, pues se puede obtener algebraicamente,

\[ \frac{df}{dx} = \frac{dx}{dx} = 1. \]

Sea ahora \(f(x)=x^2\). Entonces, para cualquier \(a\in\mathbb{R}\), se tiene que

\[ \lim_{x\to a}\frac{f(x)-f(a)}{x-a} = \lim_{x\to a}\frac{x^2-a^2}{x-a} = \lim_{x\to a}\frac{(x-a)(x+a)}{x-a} = \lim_{x\to a}x+a = 2a. \]

Por tanto, \(f(x)\) es diferenciable en todo \(\mathbb{R}\) y \(f'(a)=2a\).

Ejemplo 7.4 Sea la función \(f(x)=|x|\). Veamos si \(f\) es diferenciable en \(0\). Para ello calculamos los límites laterales.

\[\begin{align*} \lim_{x\to 0^-}\frac{f(x)-f(0)}{x-0} &= \lim_{x\to 0^-} \frac{|x|}{x} = \lim_{x\to 0^-} \frac{-x}{x} = -1,\\ \lim_{x\to 0^+}\frac{f(x)-f(0)}{x-0} &= \lim_{x\to 0^+} \frac{|x|}{x} = \lim_{x\to 0^+} \frac{x}{x} = 1, \end{align*}\]

Por tanto, como los límites laterales no coinciden, \(f\) no es diferenciable en \(0\).

Definición 7.6 (Recta tangente a la gráfica de una función) Dado un intervalo \(I\subseteq\mathbb{R}\), una función \(f:I\to\mathbb{R}\) y un punto \(a\in I\), si \(f\) es diferenciable en \(a\), se define la recta tangente a la gráfica de \(f\) en \(a\) como la recta que pasa por el punto \((a,f(a))\) con pendiente \(f'(a)\), es decir, la recta con ecuación

\[ y=f(a)+f'(a)(x-a) \]

Definición 7.7 (Recta normal a la gráfica de una función) Dado un intervalo \(I\subseteq\mathbb{R}\), una función \(f:I\to\mathbb{R}\) y un punto \(a\in I\), si \(f\) es diferenciable en \(a\), se define la recta normal a la gráfica de \(f\) en \(a\) como la recta que pasa por el punto \((a,f(a))\) y es perpendicular a la recta tangente a la gráfica de \(f\) en \(a\), es decir, la recta con ecuación

\[ y=f(a)-\frac{1}{f'(a)}(x-a) \]

Ejemplo 7.5 Dada la función \(y=f(x)=x^2\), la recta tangente a \(f\) en \(1\) es

\[ y = f(1)+f'(1)(x-1) = 1+2(x-1) = 2x-1, \]

y la recta normal es

\[ y = f(1)-\frac{1}{f'(1)}(x-1) = 1-\frac{1}{2}(x-1) = \frac{-x}{2}+\frac{3}{2}. \]

Teorema 7.1 Dado un intervalo \(I\subseteq\mathbb{R}\), una función \(f:I\to\mathbb{R}\) y un punto \(a\in I\), si \(f\) es diferenciable en \(a\) entonces \(f\) es continua en \(a\).

Prueba. Sea \(x\in I\) y \(x\neq a\). Entonces

\[ \lim_{x\to a}f(x)-f(a) = \lim_{x\to a}\frac{f(x)-f(a)}{x-a}(x-a) = \lim_{x\to a}\frac{f(x)-f(a)}{x-a}\lim_{x\to a}x-a = f'(a)\cdot 0 = 0. \]

Así pues,

\[ \lim_{x\to a}f(x)-f(a) = 0 \Rightarrow \lim_{x\to a}f(x)-\lim_{x\to a}f(a) = 0 \Rightarrow \lim_{x\to a}f(x)=\lim_{x\to a}f(a) =f(a), \] y, por tanto, \(f\) es continua en \(a\).

Precaución

El recíproco de este teorema no es cierto, es decir, pueden existir funciones continuas en un punto que no sean derivables en ese punto, como por ejemplo la función \(f(x)=|x|\) que es continua en \(0\) pero, como se ha visto, no es derivable en \(0\).

7.3 Álgebra de derivadas

Proposición 7.1 Dado un intervalo \(I\subseteq \mathbb{R}\) y dos funciones \(f,g:I\to \mathbb{R}\), si \(f\) y \(g\) son diferenciables en \(a\in I\), entonces

  1. \(f+g\) es diferenciable en \(a\) y \((f+g)'(a)=f'(a)+g'(a)\).

  2. \(f-g\) es diferenciable en \(a\) y \((f-g)'(a)=f'(a)-g'(a)\).

  3. \(c\cdot f\) es diferenciable en \(a\) y \((c\cdot f)'(a) = c\cdot f'(a)\) \(\forall c \in \mathbb{R}\).

  4. \(f\cdot g\) es diferenciable en \(a\) y \((f\cdot g)'(a) = f'(a)g(a)+f(a)g'(a)\).

  5. Si \(g(c)\neq 0\), \(\frac{f}{g}\) es diferenciable en \(a\) y \(\left(\dfrac{f}{g}\right)'(a)=\dfrac{f'(a)g(a)-f(a)g'(a)}{g(a)^2}\).

Prueba. Veamos la demostración de cada caso usando la definición de derivada.

  1. Derivada de la suma de funciones. \[\begin{align*} (f+g)'(a) &=\lim_{x\to a}\frac{(f+g)(x)-(f+g)(a)}{x-a} = \lim_{x\to a}\frac{f(x)+g(x)-f(a)-g(a)}{x-a} \\ &= \lim_{x\to a}\frac{f(x)-f(a)}{x-a}+\frac{g(x)-g(a)}{x-a} = \lim_{x\to a}\frac{f(x)-f(a)}{x-a}+\lim_{x\to a}\frac{g(x)-g(a)}{x-a}\\ &= f'(a)+g'(a). \end{align*}\]

  2. Derivada de la resta de funciones. Se prueba del mismo modo que la suma.

  3. Derivada del producto de una función por un escalar. \[\begin{align*} (c\cdot f)'(a) &=\lim_{x\to a}\frac{(c\cdot f)(x)-(c\cdot f)(a)}{x-a} = \lim_{x\to a}\frac{c\cdot f(a)-c\cdot f(a)}{x-a} \\ &= \lim_{x\to a}\frac{c(f(x)-f(a))}{x-a} = c\lim_{x\to a}\frac{f(x)-f(a)}{x-a}= c\cdot f'(a). \end{align*}\]

  4. Derivada del producto de funciones. \[\begin{align*} (f\cdot g)'(a) &=\lim_{x\to a}\frac{(f\cdot g)(x)-(f\cdot g)(a)}{x-a} = \lim_{x\to a}\frac{f(x)\cdot g(x)-f(a)\cdot g(a)}{x-a} \\ &= \lim_{x\to a}\frac{f(x)\cdot g(x)-f(a)\cdot g(x)+f(a)\cdot g(x)-f(a)\cdot g(a)}{x-a} \\ &= \lim_{x\to a}\frac{(f(x)-f(a))\cdot g(x)+f(a)(g(x)-g(a))}{x-a} \\ &= \lim_{x\to a}\frac{f(x)-f(a)}{x-a}\lim_{x\to a} g(x)+\lim_{x\to a}f(a)\lim_{x\to a}\frac{g(x)-g(a)}{x-a} = f'(a)g(a)+f(a)g'(a). \end{align*}\]

  5. Derivada del cociente de funciones. \[\begin{align*} (f\cdot g)'(a) &=\lim_{x\to a}\frac{(f/g)(x)-(f/g)(a)}{x-a} = \lim_{x\to a}\frac{f(x)/g(x)-f(a)/g(a)}{x-a} \\ &= \lim_{x\to a}\frac{\frac{f(x)g(a)-f(a)g(x)}{g(x)g(a)}}{x-a} \\ &= \lim_{x\to a}\frac{f(x)g(a)-f(a)g(x)}{(x-a)g(x)g(a)}\\ &= \lim_{x\to a} \frac{f(x)g(a)-f(a)g(a)+f(a)g(a)-f(a)g(x)}{(x-a)g(x)g(a)} \\ &= \lim_{x\to a} \frac{1}{g(x)g(a)}\left(\frac{f(x)-f(a)}{x-a}g(a) - f(a)\frac{g(x)-g(a)}{x-a}\right) \\ &= \lim_{x\to a}\frac{1}{g(x)g(a)}\left(\lim_{x\to a}g(a)\lim_{x\to a}\frac{f(x)-f(a)}{x-a}-\lim_{x\to a}f(a)\lim_{x\to a}\frac{g(x)-g(a)}{x-a}\right) \\ &= \frac{f'(a)g(a)-f(a)g'(a)}{g(a)^2}, \end{align*}\] ya que \(g(a)\neq 0\) y como \(g\) es continua en \(a\) al ser derivable en \(a\), también se puede afirmar que existe un \(\delta>0\) tal que \(g(x)\neq 0\) \(\forall x \in (a-\delta, a+\delta)\cap I\), por lo que \[ \lim_{x\to a}\frac{1}{g(x)g(a)}=\frac{1}{g(a)^2}. \]

Ejemplo 7.6 Veamos cuál es la función derivada de la función racional \(f(x)=\dfrac{x^2-2x+1}{x}\).

\[\begin{align*} f'(x) &= \frac{(x^2-2x+1)'x-(x^2-2x+1)x'}{x^2} = \frac{((x^2)'-(2x)'+1')x-(x^2-2x+1)}{x^2} = \\ &= \frac{(2x-2)x-(x^2-2x+1)}{x^2} = \frac{2x^2-2x-x^2+2x-1}{x^2} = \frac{x^2-1}{x^2} \forall x\neq 0. \end{align*}\]

7.4 Regla de la cadena

El resultado anterior permite calcular la derivada de cualquier función algebraica. A continuación se presenta otro importante resultado que nos permitirá calcular la derivada de una composición de funciones.

Teorema 7.2 (Regla de la cadena) Dados dos intervalos \(I,J\subseteq \mathbb{R}\) y dos funciones \(f:I\to \mathbb{R}\) y \(g:J\to\mathbb{R}\) tales que \(f(I)\subseteq J\), si \(f\) es diferenciable en en \(a\) y \(g\) es diferenciable en \(f(a)\), entonces \(g\circ f\) es diferenciable en \(a\) y \[ (g\circ f)'(a) = g'(f(a))f'(a). \]

Prueba. Sea

\[ h(y)= \begin{cases} \frac{g(y)-g(f(a))}{y-f(a)} & \mbox{si } y\in J \mbox{ y } y\neq f(a)\\ g'(f(a)) & \mbox{si } y=f(a) \end{cases} \]

Veamos que \(h\) es continua en \(f(a)\). Como \(g\) es diferenciable en \(f(a)\), se tiene que \(\lim_{x\to f(a)} \frac{g(x)-g(f(a))}{x-f(a)}=g'(f(a))\), de modo que para cualquier \(\varepsilon>0\) existe \(\delta>0\) tal que si \(x\in J\setminus \{f(a)\}\) y \(|x-f(a)|<\delta\), entonces \(\left|\frac{g(x)-g(f(a))}{x-f(a)}-g'(f(a))\right|<\varepsilon\). Así pues, si \(y\in J\), \(y\neq f(a)\) y \(|y-f(a)|<\delta\) entonces \(|h(y)-g'(f(a))|<\varepsilon\), y si \(y=f(a)\), entonces \(|y-f(a)|=0<\delta\) y \(|h(y)-g'(f(a))|=|g'(f(a))-g'(f(a))|=0<\varepsilon\). Por consiguiente, \(h\) es continua en \(f(a)\) y \(\lim_{y\to f(a)}h(y)=h(f(a))=g'(f(a))\).

Por otro lado, de la definición de \(h\) se tiene que \(g(y)-g(f(a))=h(y)(y-f(a))\) \(\forall y\in J\), de manera que si \(x\in I\setminus\{a\}\) y \(y=f(x)\in J\) entonces

\[\begin{align*} (g\circ f)'(a) &= \lim_{x\to a}\frac{g\circ f(x)-g\circ f(a)}{x-a} = \lim_{x\to a}\frac{g(f(x))-g(f(a))}{x-a} \\ & = \lim_{x\to a}\frac{h(f(x))(f(x)-f(a))}{x-a} = \lim_{x\to a}h(f(x))\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\\ &= h(f(a))f'(a) = g'(f(a))f'(a). \end{align*}\]

Nota

La demostración es mucho sencilla usando la notación diferencial de Leibniz para la derivada. Si \(y=g(z)\) y \(z=f(x)\), entonces

\[ \frac{dy}{dx}=\frac{dy}{dz}\frac{dz}{dx}=g'(z)f'(x)=g'(f(x))f'(x). \]

Ejemplo 7.7 Si \(g(x)=\operatorname{sen}(x)\) y \(f(x)=x^2\), entonces \(g\circ f(x)=\operatorname{sen}(x^2)\) y, aplicando la regla de la cadena, su derivada vale

\[ (g\circ f)'(x)=g'(f(x))f'(x) = \cos(g(x)) 2x = \cos(x^2)2x. \]

Por otro lado, \(f\circ g(x)= (\sin(x))^2\) y, de nuevo aplicando la regla de la cadena, su derivada vale

\[ (f\circ g)'(x)=f'(g(z))g'(z) = 2g(x)\cos(x) = 2\operatorname{sen}(x)\cos(x). \]

7.4.1 Derivada de la función inversa

La regla de la cadena nos permite calcular la derivada de la función inversa de una función.

Teorema 7.3 (Derivada de la función inversa) Dado un intervalo \(I\subseteq \mathbb{R}\) y una función \(f:I\to \mathbb{R}\) continua e inyectiva en \(I\), y sea \(J=f(I)\) y \(f^{-1}:J\to\mathbb{R}\) la función inversa de \(f\). Si \(f\) es diferenciable en \(a\in I\) y \(f'(a)\neq 0\), entonces \(f^{-1}\) es diferenciable en \(f(a)\) y

\[ (f^{-1})'(f(a)) = \frac{1}{f'(a)}. \]

Prueba. Como \(f\) es continua en \(I\), \(J=f(I)\) es un intervalo. Como además \(f\) es inyectiva, necesariamente \(f\) es monótona. Sea la función \(g(y)=\frac{y-f(a)}{f^{-1}(y)-a}\) \(\forall y\in J\setminus \{f(a)\}\). \(g\) está bien definida pues \(f^{-1}\) es inyectiva, y además, si \(y\neq f(a)\) entonces \(f^{-1}(y) \neq f^{-1}(f(a))=a\), por lo que el denominador no se anula. Veamos que \(\lim_{y\to f(a)}g(y)=f'(a)\).

Como \(f\) es diferenciable en \(a\), es decir, \(f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\), para cualquier \(\varepsilon>0\) existe \(\delta'>0\) tal que si \(|x-a|<\delta'\) entonces \(\left|\frac{f(x)-f(a)}{x-a}-f'(a)\right|<\varepsilon\).

Por otro lado, como \(f\) es continua en \(I\), \(f^{-1}\) es continua en \(J\), y en particular en \(f(a)\), es decir, \(\lim_{y\to f(a)}f^{-1}(y)=f^{-1}(f(a))=a\), de manera que para cualquier \(\delta'>0\) existe \(\delta>0\) tal que si \(y\in J\setminus\{f(a)\}\) y \(|y-f(a)|<\delta\) entonces \(|f^{-1}(y)-a|<\delta'\), y por tanto,

\[ \begin{gathered} \left|\frac{f(f^-1(y))-f(a)}{f^{-1}(y)-a}-f'(a)\right|<\varepsilon \Leftrightarrow \left|\frac{y-f(a)}{f^{-1}(y)-a}-f'(a)\right|<\varepsilon \\ \Leftrightarrow |g(y)-f'(a)|<\varepsilon \Rightarrow \lim_{y\to f(a)}g(y)=f'(a). \end{gathered} \]

Como además

\[\begin{align*} \frac{f^{-1}(y)-f^{-1}(f(a))}{y-f(a)} &= \frac{f^{-1}(y)-a}{y-f(a)} \\ &= \frac{1}{\frac{y-f(a)}{f^{-1}(y)-a}} = \frac{1}{g(y)} \label{si $y\neq f(a)$}, \end{align*}\]

y como \(\lim_{y\to f(a)}\frac{1}{g(y)} = \frac{1}{f'(a)}\), finalmente se tiene que

\[ (f^{-1})'(f(a)) = \lim_{y\to f(a)} \frac{f^{-1}(y)-f^{-1}(f(a))}{y-f(a)} = \lim_{y\to f(a)}\frac{1}{g(y)} = \frac{1}{f'(a)}. \]

Nota

De nuevo, podemos realizar la demostración del teorema de manera más sencilla utilizando la notación de diferencial de Leibniz.

\[ \frac{dx}{dy} = \frac{1}{dy/dx} = \frac{1}{f'(x)} \]

Precaución

Si en las condiciones del teorema anterior quitamos la condición \(f'(a)\neq 0\), el resultado no es cierto y \(f^{-1}\) no es diferenciable en \(f(a)\). Vamos a probarlo por reducción al absurdo. Supongamos que \(f'(a)=0\), entonces, aplicando la regla de la cadena, se tiene

\[ (f^{-1}\circ f)'(a) = (f^{-1})'(f(a))f'(a) = (f^{-1})'(f(a))0 = 0. \]

Pero, por otro lado, \((f^{-1}\circ f)'(a) = \operatorname{Id}'(a) = 1\), lo que supone una contradicción, por lo que \(f^{-1}\) no puede ser derivable en \(f(a)\).

Corolario 7.1 Dado un intervalo \(I\subseteq\mathbb{R}\) y una función \(f:I\to\mathbb{R}\) inyectiva en \(I\), y sea \(J=f(I)\) y \(f^{-1}:J\to\mathbb{R}\) la función inversa de \(f\). Si \(f\) es derivable en \(I\) y \(f'(x)\neq 0\) \(\forall x\in I\), entonces \(f^{-1}\) es derivable en \(I\) y \(\forall y\in J\),

\[ (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))} \]

Prueba. Si \(f\) es diferenciable en \(I\) entonces es continua en \(I\) y se puede aplicar el teorema anterior.

Ejemplo 7.8 La inversa de la función exponencial \(y=f(x)=e^x\) es el logaritmo neperiano \(x=f^{-1}(y)=\ln y\), de modo que, aplicando el teorema anterior, la función derivada del logaritmo es \[ \left(f^{-1}\right)'(y)=\frac{1}{f'(x)}=\frac{1}{e^x}=\frac{1}{e^{\ln y}}=\frac{1}{y}. \]

Ejemplo 7.9 Si \(n\in\mathbb{N}\) es par, la función \(f(x)=x^n\) \(\forall x\in \mathbb{R}^+\) es inyectiva y derivable, con \(f'(x)=nx^{n-1}>0\) \(\forall x\in\mathbb{R}^+\). Por tanto, la función \(f^{-1}(y)=\sqrt[n]{y}\) es derivable en \(\mathbb{R}^+\) y \(\forall y\in \mathbb{R}^+\),

\[\begin{align*} (f^{-1})'(y) &= \frac{1}{f'(f^{-1}(y))} = \frac{1}{f'(\sqrt[n]{y})} = \frac{1}{n(\sqrt[n]{y})^{n-1}} \\ &= \frac{1}{n (y^{1/n})^{n-1}} = \frac{1}{ny^{1-\frac{1}{n}}} = \frac{1}{n}y^{\frac{1}{n}-1}. \end{align*}\]

Por otro lado, si \(n\in\mathbb{N}\) es impar, la función \(f(x)=x^n\) \(\forall x\in\mathbb{R}\) es inyectiva y derivable, con \(f'(x)=nx^{n-1}\neq 0\) \(\forall x\neq 0\). Por tanto, la función \(f^{-1}(y)=\sqrt[n]{y}\) es derivable en \(\mathbb{R}\setminus\{0\}\) y, al igual que antes, \(\forall y\in \mathbb{R}^+\),

\[ (f^{-1})'(y) = \frac{1}{n}y^{\frac{1}{n}-1}. \]

7.5 Derivadas implícitas

Hasta hora siempre hemos trabajado con funciones de la forma \(y=f(x)\) donde la variable \(y\) depende de la variable \(x\) según la función \(f(x)\). Esta representación se conoce como explícita, por que la variable dependiente \(y\) aparece despejada en el lado izquierdo de la igualdad. Sin embargo, como ya se vió en la Definición 1.27, una una función real de variable real es una relación formada por pares \((x,y)\in \mathbb{R}\times\mathbb{R}\), de modo que también se puede representar de manera intensiva mediante una ecuación \(F(x,y)=0\), que cumplen los puntos de la función y solo ellos.

Ejemplo 7.10 La función \(y=x^2\) también se puede expresar implícitamente mediante la ecuación \(y-x^2=0\).

Precaución

El problema de la representación implícita es que no toda ecuación en \(x\) e \(y\) define una función. Por ejemplo, la ecuación \(y^2-x=0\) no define una función, ya que si se despeja \(y\) de la ecuación se obtiene \(y=\pm\sqrt{x}\), que no es una función ya que para cualquier valor de \(x>0\), \(y\) puede tomar dos valores, lo cual no está permitido en una función.

Dada una ecuación \(F(x,y)=0\), que define implícitamente \(y\) como función de \(x\), si \(y\) es derivable en un punto \((x_0, y_0)\), se puede calcular la derivada mediante el siguiente procedimiento:

  1. Calcular la derivada de las expresiones de ambos lados de la ecuación. \(F'(x,y)=0\). En el cálculo de estas derivadas hay que tener en cuenta que \(y\) es una función que depende de \(x\) y aplicar la regla de la cadena para derivarla.

  2. Reescribir la ecuación de manera que los términos donde aparezca \(y'\) queden a un lado de la ecuación y el resto al otro.

  3. Sacar \(y'\) factor común en el lado de la ecuación donde aparezca.

  4. Resolver la ecuación para \(y'\).

  5. Sustituir \(x=x_0\), \(y=y_0\).

Ejemplo 7.11 Dada la ecuación \(e^y-x^2=0\) que define a \(y\) como función implícita de \(x\), veamos cómo calcular su derivada en el punto \((1,0)\) implícitamente

\[\begin{align*} (e^y-x^2)' = 0' &\Rightarrow e^yy'-2x = 0 \Rightarrow e^yy' = 2x \Rightarrow y' = \frac{2x}{e^y}. \end{align*}\]

Sustituyendo \(x=1\) e \(y=0\), se tiene \(y'(1) = \frac{2\cdot 1}{e^0} = 2\).

En este caso, es posible obtener la representación explícita de la función, ya que \(e^y-x^2=0 \Rightarrow e^y=x^2 \Rightarrow y=\ln(x^2) = 2\ln(x)\). Si calculamos su derivada explícitamente, se tiene \(y'=\frac{2}{x}\), y para \(x=1\) se tiene \(y'(1) = \frac{2}{1}=2\), que coincide con el resultado anterior.

Aún cuando la ecuación \(F(x,y)=0\) no defina implícitamente a \(y\) como función de \(x\), es posible utiliza el procedimiento anterior para estudiar la tasa de variación instantánea de \(y\) con respecto a \(x\) en un punto \((x_0, y_0)\) que cumpla la ecuación.

Ejemplo 7.12 La ecuación \(x^2-xy+y^2=1\) no define a \(y\) como función explícita de \(x\), ya que para \(x=0\) se obtienen dos posibles valores de \(y\), \(0^2-0\cdot y+y^2=1 \Rightarrow y^2=1 \Rightarrow y=\pm 1\). No obstante, en el punto \((0,1)\), se puede calcular la tasa de variación instantánea de \(y\) con respecto a \(x\),

\[ \begin{gathered} (x^2-xy+y^2)' = 1' \Rightarrow (x^2)'-(xy)'+(y^2)' = 0 \\ \Rightarrow 2x -(1\cdot y+xy')+2yy' = 0 \Rightarrow 2x-y-xy'+2yy'=0 \\ \Rightarrow y'(-x+2y)=-2x+y \Rightarrow y'=\frac{-2x+y}{-x+2y}, \end{gathered} \]

y sustituyendo \(x=0\), \(y=1\) se tiene \(y'(0)=\frac{-2\cdot 0+1}{-0+2\cdot 1} = \frac{1}{2}\).

Si dibujamos la gráfica de los puntos que cumplen la ecuación, se puede comprobar que la recta tangente a la gráfica en el punto \((0,1)\) tiene pendiente \(1/2\).

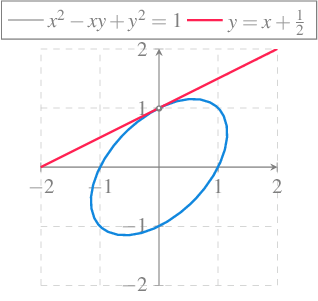
Recta tangente a la curva implícita \(x^2-xy+y^2=1\) en el punto \((0,1)\).

7.6 Teorema del valor medio y aplicaciones

Teorema 7.4 (Extremo interior) Dado un intervalo \(I\subseteq \mathbb{R}\) y una función \(f:I\to\mathbb{R}\) con un extremo relativo en un punto interior \(a\in I\), si \(f\) es diferenciable en \(a\), entonces \(f'(a)=0\).

Prueba. Supongamos que \(f\) tiene un máximo relativo en \(a\in I\). Por ser \(a\) un punto interior de \(I\), existe un \(\delta>0\) tal que el entorno \((a-\delta, a+\delta)\subset I\) y \(f(x)<f(a)\) \(\forall x\in (a-\delta,a+\delta)\).

Supongamos ahora que \(f'(a)>0\). Como \(f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\), existe un \(0<\delta'<\delta\) tal que \(\frac{f(x)-f(a)}{x-a}>0\) \(\forall x\in (a-\delta',a+\delta')\setminus\{a\}\). Por tanto, si \(x\in (a,a+\delta')\), \(f(x)-f(a)>0\) de donde se deduce que \(f(x)>f(a)\) lo que contradice que \(f\) tenga un máximo relativo en \(a\). Así que no puede ser \(f'(c)>0\).

Del mismo modo se puede probar que no puede ser \(f'(a)<0\). Por lo que necesariamente tiene que ser \(f'(a)=0\).

Si \(f\) tiene un mínimo relativo en \(a\), la demostración es análoga.

Precaución

El resultado anterior no es cierto si el punto \(a\) no es interior de \(I\). Para verlo, basta considerar \(f(x)=x\) \(\forall x\in[0,1]\). Se observa que \(f\) tiene un máximo relativo en \(1\), pero \(f'(1)\neq 0\).

Corolario 7.2 Dado un intervalo \(I\subseteq \mathbb{R}\) y una función \(f:I\to\mathbb{R}\) con un extremo relativo en un punto \(a\in I\), entonces \(f'(a)\) no existe o \(f'(a)=0\).

Ejemplo 7.13 La función \(f(x)=|x|\) tiene un mínimo relativo en \(0\) que es un punto interior de \(\mathbb{R}\). Sin embargo, \(f'(0)\) no existe.

Definición 7.8 (Punto crítico) Dado un intervalo \(I\subseteq\mathbb{R}\) y una función \(f:I\to\mathbb{R}\), se dice que \(a\) es un punto crítico o punto singular de \(f\), si \(f'(a)=0\).

Gráficamente, los puntos críticos son puntos donde la tangente a la gráfica de la función es horizontal.

Como veremos más adelante, los puntos críticos juegan un papel clave en la determinación de los extremos relativos de una función.

Teorema 7.5 (Rolle) Dada una función \(f:[a,b]\to\mathbb{R}\) continua en \([a,b]\) y diferenciable en \((a,b)\), si \(f(a)=f(b)\), entonces \(f\) tiene al menos un punto crítico en \((a,b)\), es decir, existe \(c\in(a,b)\) tal que \(f'(c)=0\).

Prueba. Como \(f\) es continua en \([a,b]\), por el Teorema 6.10 \(f\) alcanza el máximo y el mínimo en \([a,b]\). Si existe \(c\in (a,b)\) tal que \(f\) alcanza el máximo o el mínimo en \(c\), por el teorema anterior se tiene \(f'(c)=0\). En caso contrario, si no existe \(c\in(a,b)\) tal que \(f\) alcanza el máximo o el mínimo en \(c\), entonces \(f\) alcanza el máximo o el mínimo en los extremos del intervalo, pero como \(f(a)=f(b)\), se deduce que que \(f\) es constante en \([a,b]\) y, por tanto, \(f'(x)=0\) \(\forall x\in (a,b)\).

Teorema 7.6 (Valor medio) Dada una función \(f:[a,b]\to\mathbb{R}\) continua en \([a,b]\) y diferenciable en \((a,b)\), entonces existe \(c\in (a,b)\) tal que

\[ f'(c) = \frac{f(b)-f(a)}{b-a}. \]

Prueba. Sea \(g(x)\) la recta secante a \(f\) en los puntos \((a,f(a))\) y \((b,f(b))\). Entonces \(g(x)=f(a)+\operatorname{TVM}(f,[a,b])(x-a) = f(a)+\frac{f(b)-f(a)}{b-a}(x-a)\). Si tomamos la función que mide la distancia entre \(f\) y \(g\), es decir, \(\forall x\in[a,b]\)

\[ h(x)=f(x)-g(x)= f(x)-f(a)+\frac{f(b)-f(a)}{b-a}(x-a), \]

\(h\) es continua en \([a,b]\) por ser la diferencia de dos funciones continuas en ese intervalo, también es derivable en \((a,b)\) al ser \(f\) y \(g\) derivables en el intervalo. Además

\[\begin{align*} h(a) &= f(a) - f(a)+\frac{f(b)-f(a)}{b-a}(a-a) = 0,\\ h(b) &= f(a) - f(b)+\frac{f(b)-f(a)}{b-a}(b-a) = 0.\\ \end{align*}\]

Por tanto, aplicando el teorema de Rolle, existe \(c\in(a,b)\) tal que \(f'(c)=0\). Como

\[ h'(x) = f'(x) - \frac{f(b)-f(a)}{b-a} \ \forall x\in (a,b), \]

en particular se tiene

\[ h'(c) = f'(c) - \frac{f(b)-f(a)}{b-a} = 0 \Rightarrow f'(c) = \frac{f(b)-f(a)}{b-a}. \]

7.6.1 Estudio del crecimiento de una función

La principal aplicación de la derivada es el estudio del crecimiento de una función mediante el signo de la derivada.

Teorema 7.7 (Signo de la derivada) Dado un intervalo \(I\subseteq\mathbb{R}\) y una función \(f:I\to\mathbb{R}\) diferenciable en \(I\), entonces:

  1. \(f\) es creciente en \(I\) si y sólo si \(f'(x)\geq 0\) \(\forall x\in I\).
  2. \(f\) es decreciente en \(I\) si y sólo si \(f'(x)\leq 0\) \(\forall x\in I\).

Prueba. Probaremos solo el primer apartado, ya que el segundo se prueba de forma análoga.

Supongamos que \(f\) es creciente en \(I\) y sea \(a\in I\). Si \(x\in I\) y \(x>a\), por ser \(f\) creciente, \(f(x)>f(a)\), por lo que \(\frac{f(x)-f(a)}{x-a}\geq 0\). Y si \(x<a\), \(f(x)<f(a)\), por lo que también se tiene \(\frac{f(x)-f(a)}{x-a}\geq 0\). Así pues, \(f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\geq 0\).

Para ver el otro sentido de la implicación, supongamos que \(f'(x)\geq 0\) \(\forall x\in I\), y sean \(a,b\in I\) con \(a<b\). Aplicando el teorema del valor medio a \(f\) en el intervalo \([a,b]\), se tiene que existe \(c\in(a,b)\) tal que \(f'(c)= \frac{f(b)-f(a)}{b-a}\geq 0\), y como \(b-a>0\), se tiene que \(f(b)-f(a)>0\) por lo que \(f(b)>f(a)\) y, por tanto, \(f\) es creciente en \(I\).

Ejemplo 7.14 La función \(f(x)=x^3\) es creciente en todo \(\mathbb{R}\) ya que \(\forall x\in \mathbb{R}\ f'(x)\geq 0\).

Advertencia

Una función puede ser creciente o decreciente en un intervalo y no tener derivada.

Ejemplo 7.15 Consideremos la función \(f(x)=x^4-2x^2+1\). Su derivada \(f'(x)=4x^3-4x\) está definida en todo \(\mathbb{R}\) y es continua.

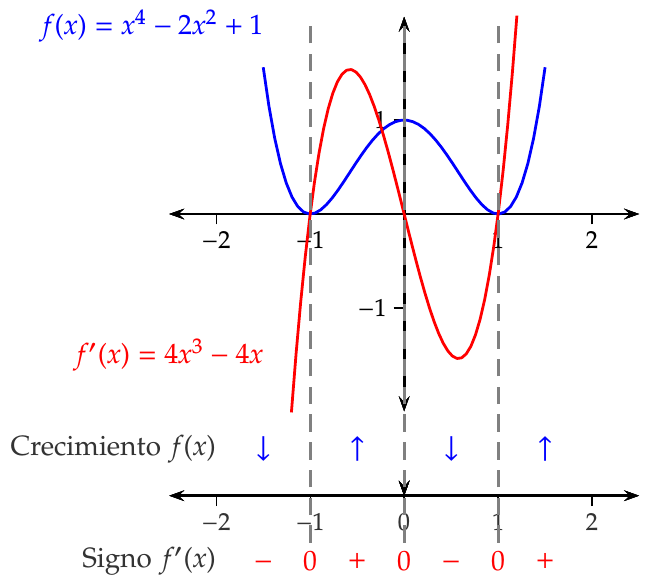
Estudio del crecimiento de una función.

7.6.2 Determinación de los extremos relativos de una función

Como consecuencia del resultado anterior, la derivada también sirve para determinar los extremos relativos de una función.

Teorema 7.8 (Criterio de la primera derivada) Sea una función \(f:[a,b]\to\mathbb{R}\) continua en \([a,b]\) y derivable en \((a,c)\cup (c,b)\) para un punto \(c\in(a,b)\).

  1. Si existe un \(\delta>0\) tal que \((c-\delta, c+\delta)\subseteq[a,b]\) y \(f'(x)\geq 0\) y \(\forall x\in(c-\delta,c)\) y \(f'(x)\leq 0\) \(\forall x\in(c,c+\delta)\), entonces \(f\) tiene un máximo relativo en \(c\).
  2. Si existe un \(\delta>0\) tal que \((c-\delta, c+\delta)\subseteq[a,b]\) y \(f'(x)\leq 0\) y \(\forall x\in(c-\delta,c)\) y \(f'(x)\geq 0\) \(\forall x\in(c,c+\delta)\), entonces \(f\) tiene un mínimo relativo en \(c\).

Prueba. Demostraremos solo el caso de un máximo, ya que el otro caso es análogo. Para ver que \(f\) tiene un máximo local en \(c\) basta con probar que si \(x\in(c-\delta,c+\delta)\) entonces \(f(x)\leq f(c)\).

Si \(x\in(c-\delta,c)\) entonces \(f'(x)\geq 0\). Aplicando el teorema del valor medio a \(f\) en el intervalo \([x,c]\) se tiene que existe \(u\in(x,c)\) tal que \(f'(u)=\frac{f(c)-f(x)}{c-x}\geq 0\), y como \(c-x>0\) se concluye que \(f(c)-f(x)\geq 0\), y por tanto, \(f(x)\leq f(c)\).

Y si Si \(x\in(c, c+\delta)\) entonces \(f'(x)\leq 0\). Aplicando de nuevo el teorema del valor medio a \(f\) en el intervalo \([c,x]\) se tiene que existe \(v\in(c,x)\) tal que \(f'(v)=\frac{f(x)-f(c)}{x-c}\leq 0\), y como \(x-c>0\) se concluye que \(f(x)-f(c)\leq 0\), y por tanto, \(f(x)\leq f(c)\).

Ejemplo 7.16 Consideremos de nuevo la función \(f(x)=x^4-2x^2+1\). Su derivada \(f'(x)=4x^3-4x\) está definida en todo \(\mathbb{R}\) y es continua.

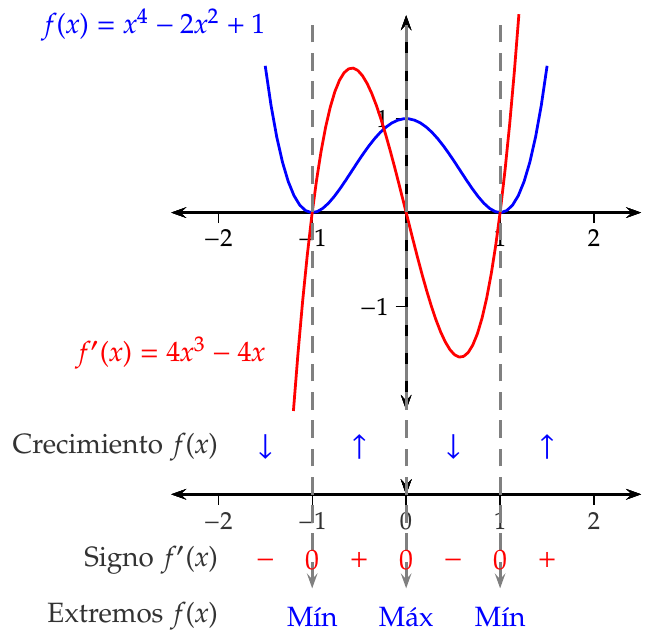
Estudio de los extremos de una función
Precaución

El recíproco de las implicaciones del teorema anterior no tiene por qué ser cierto. Por ejemplo, la función

\[ f(x)= \begin{cases} 2x^4+x^4\operatorname{sen}\left(\frac{1}{x}\right) & \mbox{si } x\neq 0,\\ 0 & \mbox{si } x=0. \end{cases} \]

tiene un mínimo relativo y absoluto en \(x=0\), pero su derivada toma valores positivos y negativos en cualquier entorno de \(0\).

Teorema 7.9 (Darboux) Dada una función \(f:[a,b]\to\mathbb{R}\), si \(f\) es diferenciable en \([a,b]\) y \(f'(a)<k<f'(b)\), entonces existe \(c\in(a,b)\) tal que \(f'(c)=k\).

Prueba. Definimos \(g(x)=k(x-a)-f(x)\) \(\forall x\in[a,b]\). \(g\) es diferenciable en \([a,b]\) al serlo \(f\) y \(g'(x)=k-f'(x)\) \(\forall x\in[a,b]\). Por tanto, \(g\) es continua en \([a,b]\), y entonces tiene un máximo y un mínimo relativos en \([a,b]\).

Por otro lado, \(g'(a)=k-f'(a)>0\), de manera que \(g\) no tiene un máximo relativo en \(a\), y \(g'(b)=k-f'(b)<0\), de manera que \(g\) tampoco tiene un máximo relativo en \(b\). Por tanto, \(g\) alcanza el máximo relativo en un punto \(c\in (a,b)\), y por el teorema del extremo interior, \(g'(c)=0\), de donde se deduce que \(k-f(c)=0\), y \(f'(c)=k\).

7.6.3 Determinación de los extremos absolutos de una función

Ya se vió, por el Teorema 6.10, que una función continua en un intervalo cerrado \([a,b]\) alcanza el máximo y el mínimo absolutos en ese intervalo. Así pues, para encontrar los extremos absolutos de una función \(f\) derivable en \([a,b]\), basta con seguir el siguiente procedimiento:

  1. Calcular los puntos críticos de \(f\).
  2. Calcular los valores de \(f\) en los puntos críticos.
  3. Calcular el valor de \(f\) en los extremos del intervalo, \(a\) y \(b\).
  4. El máximo absoluto será el mayor de los valores obtenidos en los pasos 2 y 3, y el mínimo absoluto será el menor de los valores obtenidos en esos mismos pasos.

Ejemplo 7.17 Veamos cuáles son los extremos absolutos de la función \(f(x)=x^4-2x^2+1\) en el intervalo \([0,2]\). Seguiremos el procedimiento anterior para la determinación de los extremos absolutos.

  1. En el Ejemplo 12.22 se vió que \(f\) tenía tres puntos críticos en \(-1\), \(0\) y \(1\). El punto crítico en \(-1\) se puede descartar al no pertenecer al intervalo \([0,2]\).

  2. El valor de la función en los puntos críticos del intervalo \([0,2]\) son \(f(0)=1\) y \(f(1)=0\).

  3. El valor de la función en los extremos del intervalo \([0,2]\) es \(f(0)=1\) y \(f(2)=9\).

  4. El máximo absoluto de \(f\) en \([a,b]\) es \(\max\{f(0),f(1),f(2)\}=\max\{1,0,9\}=9\) y el mínimo absoluto es \(\min\{f(0),f(1),f(2)\}=\max\{1,0,9\}=0\).

7.6.4 Otras aplicaciones del teorema del valor medio

Además del estudio del crecimiento de una función y de la determinación de sus extremos relativos, el teorema del valor medio tiene otras muchas aplicaciones como las que se enumeran a continuación.

7.6.4.1 Localización de raíces

Si una función \(g\) es la derivada de otra función \(f\), el teorema de Rolle nos asegura que entre dos raíces cualesquiera de \(f\) existe al menos una raíz de \(g\).

Ejemplo 7.18 La función \(g(x)=\cos(x)\) es la derivada de la función \(f(x)=\operatorname{sen}(x)\), de manera que, entre dos raíces cualesquiera de \(\operatorname{sen}(x)\) existe al menos una raíz de \(\cos(x)\).

7.6.4.2 Desigualdades

El teorema del valor medio se puede usar en la obtención de desigualdades tales como \(-x\leq \operatorname{sen}(x)\leq x\), donde la igualdad se da para \(x=0\) y la desigualdad se cumple para \(x>0\).

Ejemplo 7.19 Sea \(f(x)=\operatorname{sen}(x)\) cuya derivada es \(f'(x)=\cos(x)\) \(\forall x\in\mathbb{R}\). Aplicando el teorema del valor medio a \(f\) en el intervalo \([0,x]\) para \(x>0\), se tiene que \(\frac{\operatorname{sen}(x)-\operatorname{sen}(0)}{x-0} = \cos(c)\) para algún \(c\in(0,x)\). Como \(\operatorname{sen(0)}=0\) y \(-1\leq \cos(x)\leq 1\) \(\forall x\in \mathbb{R}\), se tiene \(\operatorname{sen}(x)=\cos(c)x\) para algún \(c\in(0,x)\), de lo que se deduce que \(-x\leq \operatorname{sen}(x)\leq x\).

7.6.4.3 Estimación de errores

Otra interesante aplicación es el cálculo aproximado del valor de una función en un punto \(c\in (a,b)\), si se conoce el valor de la función en \(a\) y \(b\).

Ejemplo 7.20 Veamos cómo calcular \(\sqrt{105}\) de manera aproximada. Para ello tomamos la función \(f(x)=\sqrt{x}\) que es derivable en todo \(\mathbb{R}\) con derivada \(f'(x)=\frac{1}{2\sqrt{x}}\). Aplicando el teorema del valor medio en el intervalo \([100, 105]\) se tiene que \(\frac{\sqrt{105}-\sqrt{100}}{105-100}=\frac{1}{2\sqrt{c}}\) para algún \(c\in(100,105)\).

Por otro lado, como \(f\) es creciente, se tiene que \(10=\sqrt{100}<\sqrt{c}<\sqrt{121}=11\). Así pues, se tiene

\[\begin{align*} \frac{\sqrt{105}-\sqrt{100}}{105-100}=\frac{1}{2\sqrt{c}} & \Rightarrow \sqrt{105}-10 = \frac{5}{2\sqrt{c}} \\ & \Rightarrow \frac{5}{2\cdot 11}< \sqrt{105}-10 < \frac{5}{2\cdot 10} \\ &\Rightarrow 10.22<\sqrt{105}<10.25. \end{align*}\]

7.7 Estudio de la concavidad de una función

Como se ha visto, la derivada de una función puede utilizarse para estudiar el crecimiento de la función en un intervalo, de manera que si la función es dos veces derivable en el intervalo, es decir, si existe la derivada de la derivada de la función, la segunda derivada puede utilizarse para estudiar el crecimiento de la primera, y esto permite estudiar la concavidad de la función.

Teorema 7.10 (Criterio de la segunda derivada) Dado un intervalo \(I\subseteq\mathbb{R}\) abierto y una función \(f:I\to\mathbb{R}\) dos veces diferenciable en \(I\). Entonces,

  1. \(f\) es cóncava hacia arriba en \(I\), si y sólo si, \(f''(x)\geq 0\) \(\forall x\in I\).
  2. \(f\) es cóncava hacia abajo en \(I\), si y sólo si, \(f''(x)\leq 0\) \(\forall x\in I\).

Prueba. Daremos un prueba informal del primer apartado, ya que el segundo se prueba de manera análoga por simetría, ya que si \(f\) es cóncava hacia abajo, \(-f\) es cóncava hacia arriba.

Si \(f\) es cóncava hacia arriba en \(I\), para cualquier \(a,b\in I\) con \(a<b\), la pendiente de la recta tangente en \((a,f(a))\) es menor que la pendiente de la recta tangente en \((b,f(b))\), por lo que las pendientes crecen. Como la pendiente de la recta tangente es la derivada, se concluye que \(f'\) es creciente en \(I\) y, por tanto, \(f''(x)\geq 0\) \(\forall x\in I\).

Ejemplo 7.21 La función \(f(x)=x^2\) tiene segunda derivada \(f''(x)=2>0\) y por tanto es cóncava en todo \(\mathbb{R}\).

Advertencia

Una función puede ser cóncava hacia arriba o hacia abajo en un intervalo y no tener derivada.

Ejemplo 7.22 Consideremos de nuevo la función \(f(x)=x^4-2x^2+1\). Su segunda derivada \(f''(x)=12x^2-4\) está definida en todo \(\mathbb{R}\) y es continua.

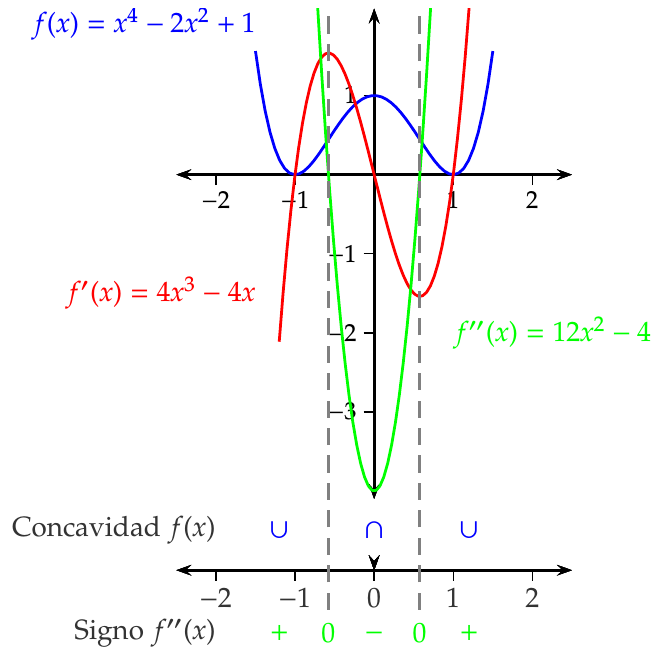
Estudio de la concavidad de una función.

7.8 Interpretación cinemática de la derivada

7.8.1 Movimiento rectilíneo

Cuando una función \(f(t)\) describe la posición de un objeto móvil sobre la recta real en el instante \(t\), tomando como referencia el origen de coordenadas \(O\) y el vector unitario \(\mathbf{i}=(1)\), se puede representar la posición \(P\) del móvil en cada instante \(t\) mediante un vector \(\vec{OP}=x\mathbf{i}\) donde \(x=f(t)\).

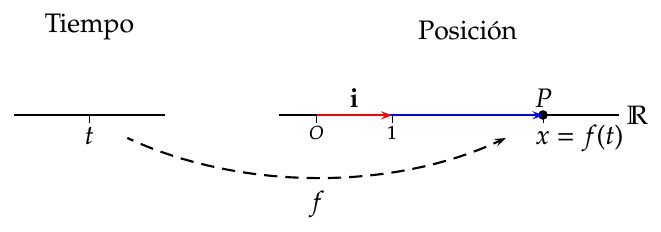
Interpretación cinemática del movimiento rectilíneo.

En este contexto, si se toman los instantes \(t=t_0\) y \(t=t_0+\Delta t\), ambos del dominio \(I\) de \(f\), el vector

\[\mathbf{v}_m=\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}\]

que se conoce como velocidad media del espacio recorrido por \(f\) entre los instantes \(t_0\) y \(t_0+\Delta t\).

Ejemplo 7.23 Un vehículo realiza un viaje de Madrid a Barcelona. Sea \(f(t)\) la función que da la posición el vehículo en cada instante \(t\). Si el vehículo parte de Madrid (km 0) a las 8 y llega a Barcelona (km 600) a las 14 horas, entonces la velocidad media del vehículo en el trayecto es

\[ \mathbf{v}_m=\frac{f(14)-f(8)}{14-8}=\frac{600-0}{6} = 100 \mbox{ km/h}. \]

Siguiendo en este mismo contexto del movimiento rectilíneo, la derivada de \(f\) en el instante \(t=t_0\) es el vector

\[ \mathbf{v}=f'(t_0)=\lim_{\Delta x\rightarrow 0}\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}, \]

que se conoce, siempre que exista el límite, como velocidad instantánea o simplemente la velocidad del espacio recorrido por \(f\) en el instante \(t_0\).

Es decir, la derivada de la posición respecto del tiempo, es un campo de vectores que recibe el nombre de velocidad a lo largo de la trayectoria \(f\).

Siguiendo con el ejemplo anterior, lo que marca el velocímetro en un determinado instante sería el módulo del vector velocidad en ese instante.

Nota

También tiene sentido pensar en \(f(t)\) como una función que mide otras magnitudes como por ejemplo la temperatura de un cuerpo, la concentración de un gas, la cantidad de un compuesto en una reacción química o el precio de las acciones de una compañía en cada instante \(t\).

7.8.2 Generalización al movimiento curvilíneo

La derivada como velocidad a lo largo de una trayectoria en la recta real puede generalizarse a trayectorias en cualquier espacio euclídeo \(\mathbb{R}^n\).

Para el caso del plano real \(\mathbb{R}^2\), si \(f(t)\) describe la posición de un objeto móvil en el plano en el instante \(t\), tomando como referencia el origen de coordenadas \(O\) y los vectores coordenados \(\{\mathbf{i}=(1,0),\mathbf{j}=(0,1)\}\), se puede representar la posición \(P\) del móvil en cada instante \(t\) mediante un vector \(\vec{OP}=x(t)\mathbf{i}+y(t)\mathbf{j}\) cuyas coordenadas

\[ \begin{cases} x=x(t)\\ y=y(t) \end{cases} \quad t\in I\subseteq \mathbb{R} \]

se conocen como funciones coordenadas de \(f\) y se escribe \(f(t)=(x(t),y(t))\).

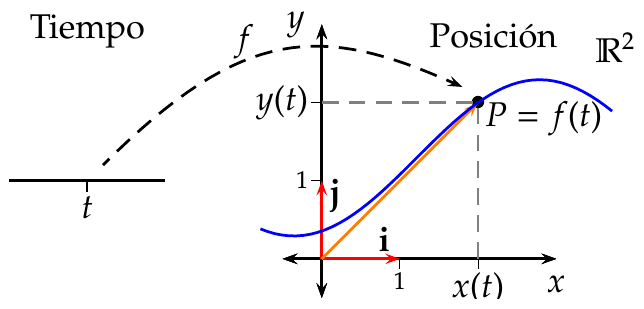
Interpretación cinemática del movimiento curvilineo.

7.8.2.1 Velocidad en una trayectoria curvilínea en el plano

En este contexto de una trayectoria \(f(t)=(x(t),y(t))\) en el plano real \(\mathbb{R}^2\), para un instante \(t=t_0\), si existe el vector

\[ \mathbf{v} = \lim_{\Delta t\rightarrow 0} \frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}, \]

entonces \(f\) es derivable en el instante \(t=t_0\) y el vector \(\mathbf{v}=f'(t_0)\) se conoce como velocidad de \(f\) en ese instante.

Como \(f(t)=(x(t),y(t))\),

\[\begin{align*} f'(t)&=\lim_{\Delta t\rightarrow 0} \frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}\\ &= \lim_{\Delta t\rightarrow 0} \frac{(x(t_0+\Delta t),y(t_0+\Delta t))-(x(t_0),y(t_0))}{\Delta t} \\ &= \lim_{\Delta t\rightarrow 0} \left(\frac{x(t_0+\Delta t)-x(t_0)}{\Delta t},\frac{y(t_0+\Delta t)-y(t_0)}{\Delta t}\right) =\\ &= \left(\lim_{\Delta t\rightarrow 0}\frac{x(t_0+\Delta t)-x(t_0)}{\Delta t},\lim_{\Delta t\rightarrow 0}\frac{y(t_0+\Delta t)-y(t_0)}{\Delta t}\right) \\ &= (x'(t_0),y'(t_0)). \end{align*}\]

luego

\[ \mathbf{v} = x'(t_0)\mathbf{i}+y'(t_0)\mathbf{j}. \]

Ejemplo 7.24 Dada la trayectoria \(f(t) = (\cos(t),\operatorname{sen}(t))\), \(t\in \mathbb{R}\), cuya imagen es la circunferencia de centro el origen de coordenadas y radio 1, sus funciones coordenadas son \(x(t) = \cos(t)\), \(y(t) = \operatorname{sen}(t)\), \(t\in \mathbb{R}\), y su velocidad es

\[ \mathbf{v}=f'(t)=(x'(t),y'(t))=(-\operatorname{sen}(t), \cos(t). \]

En el instante \(t=\pi/4\), el móvil estará en la posición \(f(\pi/4) = (\cos(\pi/4),\operatorname{sen}(\pi/4)) =(\sqrt{2}/2,\sqrt{2}/2)\) y se moverá con una velocidad \(\mathbf{v}=f'(\pi/4)=(-\operatorname{sen}(\pi/4),\cos(\pi/4))=(-\sqrt{2}/2,\sqrt{2}/2)\).

Trayectoria de la circunferencia.

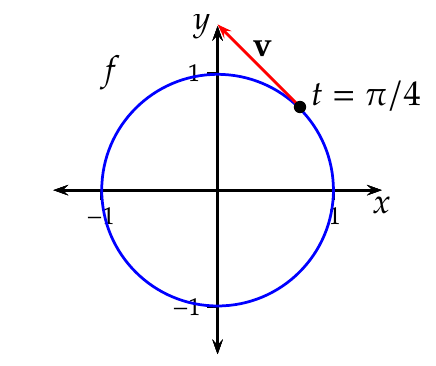
Obsérvese que el módulo del vector velocidad siempre será 1 ya que \(\lvert \mathbf{v}\rvert = \sqrt{(-\operatorname{sen}(t))^2+(\cos(t))^2}=1\).

7.9 Recta tangente a una trayectoria

7.9.1 Recta tangente a una trayectoria en el plano

Los vectores paralelos a la velocidad \(\mathbf{v}\) se denominan vectores tangentes a la trayectoria \(f\) en el instante \(t=t_0\), y la recta que pasa por \(P=f(t_0)\) dirigida por \(\mathbf{v}\) es la recta tangente a \(f\) cuando \(t=t_0\).

Definición 7.9 (Recta tangente a una trayectoria) Dada una trayectoria \(f\) sobre el plano real \(\mathbb{R}^2\), se llama recta tangente a \(f\) en \(t=t_0\) a la recta de ecuación

\[\begin{align*} l: (x,y)&= f(t_0)+tf'(t_0) = (x(t_0),y(t_0))+t(x'(t_0),y'(t_0))\\ &= (x(t_0)+tx'(t_0),y(t_0)+ty'(t_0)). \end{align*}\]

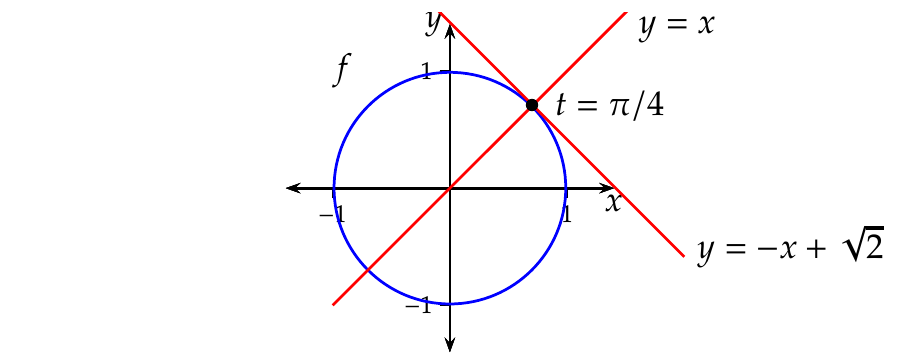
Ejemplo 7.25 Se ha visto que para la trayectoria \(f(t) = (\cos(t),\operatorname{sen}(t))\), \(t\in \mathbb{R}\), cuya imagen es la circunferencia de centro el origen de coordenadas y radio 1, en el instante \(t=\pi/4\) la posición del móvil era \(f(\pi/4)=(\sqrt{2}/2,\sqrt{2}/2)\) y su velocidad \(\mathbf{v}=(-\sqrt{2}/2,\sqrt{2}/2)\), de modo que la recta tangente a \(f\) en ese instante es

\[\begin{align*} l &: X=f(\pi/2)+t\mathbf{v} = \left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)+t\left(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right) \\ &= \left(\frac{\sqrt{2}}{2}-t\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2}\right). \end{align*}\]

De la ecuación vectorial de la recta tangente a \(f\) para \(t=t_0\), se obtiene que sus funciones cartesianas son

\[ s\begin{cases} x=x(t_0)+tx'(t_0)\\ y=y(t_0)+ty'(t_0) \end{cases} \quad t\in \mathbb{R}, \]

y despejando \(t\) en ambas ecuaciones e igualando se llega a la ecuación cartesiana de la recta tangente

\[ \frac{x-x(t_0)}{x'(t_0)}=\frac{y-y(t_0)}{y'(t_0)}, \]

si \(x'(t_0)\neq 0\) e \(y'(t_0)\neq 0\), y de ahí a la ecuación en la forma punto-pendiente

\[ y-y(t_0)=\frac{y'(t_0)}{x'(t_0)}(x-x(t_0)). \]

Partiendo de la ecuación vectorial de la tangente del ejemplo anterior \(l=\left(\frac{\sqrt{2}}{2}-t\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2}\right)\), su ecuación cartesiana es

\[ \begin{gathered} \frac{x-\sqrt{2}/2}{-\sqrt{2}/2} = \frac{y-\sqrt{2}/2}{\sqrt{2}/2}\Rightarrow\\ y-\sqrt{2}/2 = \frac{-\sqrt{2}/2}{\sqrt{2}/2}(x-\sqrt{2}/2) \Rightarrow \\ y=-x+\sqrt{2}. \end{gathered} \]

7.9.2 Recta normal a una trayectoria en el plano

Se ha visto que la recta tangente a una trayectoria \(f\) cuando \(t=t_0\) es la recta que pasa por el punto el punto \(P=f(t_0)\) dirigida por el vector velocidad \(\mathbf{v}=f'(t_0)=(x'(t_0),y'(t_0))\). Si en lugar de tomar ese vector se toma como vector director el vector \(\mathbf{w}=(y'(t_0),-x'(t_0))\), que es ortogonal a \(\mathbf{v}\), se obtiene otra recta que se conoce como recta normal a la trayectoria \(f\) cuanto \(t=t_0\).

Definición 7.10 (Recta normal a una trayectoria) Dada una trayectoria \(f\) sobre el plano real \(\mathbb{R}^2\), se llama recta normal a \(f\) en \(t=t_0\) a la recta de ecuación

\[\begin{align*} l: (x,y) &= (x(t_0),y(t_0))+t(y'(t_0),-x'(t_0)) =\\ &= (x(t_0)+ty'(t_0),y(t_0)-tx'(t_0)). \end{align*}\]

Su ecuación cartesiana es

\[ \frac{x-x(t_0)}{y'(t_0)} = \frac{y-y(t_0)}{-x'(t_0)}, \]

y su ecuación en la forma punto pendiente

\[ y-y(t_0) = \frac{-x'(t_0)}{y'(t_0)}(x-x(t_0)). \]

Importante

La recta normal es perpendicular a la recta tangente ya que sus vectores directores son ortogonales.

Ejemplo 7.26 Siguiendo con el ejemplo de la trayectoria \(f(t) = (\cos(t),\operatorname{sen}(t))\), \(t\in \mathbb{R}\), la recta normal en el instante \(t=\pi/4\) es

\[\begin{align*} l&: (x,y)=(\cos(\pi/2),\operatorname{sen}(\pi/2))+t(\cos(\pi/2),\operatorname{sen}(\pi/2)) =\\ & \left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)+t\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right) =\left(\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2}\right), \end{align*}\]

y su ecuación cartesiana es

\[ \frac{x-\sqrt{2}/2}{\sqrt{2}/2} = \frac{y-\sqrt{2}/2}{\sqrt{2}/2}\Rightarrow y-\sqrt{2}/2 = \frac{\sqrt{2}/2}{\sqrt{2}/2}(x-\sqrt{2}/2) \Rightarrow y=x. \]

Tangente y normal a la trayectoria de una circunferencia.

7.9.3 Rectas tangente y normal a una función

Un caso particular de las recta tangente y normal a una trayectoria son la recta tangente y normal a una función de una variable real. Si se tiene la función \(y=f(x)\), \(x\in I\subseteq \mathbb{R}\), una trayectoria que traza la gráfica de \(f\) es \(g(t) = (t,f(t)) \quad t\in I,\) y su velocidad es \(g'(t) = (1,f'(t)),\) de modo que la recta tangente para \(t=a\) es

\[ \frac{x-a}{1} = \frac{y-f(a)}{f'(a)} \Rightarrow y-f(a) = f'(a)(x-a), \]

y la recta normal es

\[ \frac{x-a}{f'(a)} = \frac{y-f(a)}{-1} \Rightarrow y-f(a) = \frac{-1}{f'(a)}(x-a), \]

Ejemplo 7.27 Dada la función \(y=f(x)=x^2\), la trayectoria que dibuja la gráfica de esta función es \(g(t)=(t,t^2)\) y su velocidad es \(g'(t)=(1,2t)\), de modo que en el punto \((1,1)\), que se alcanza en el instante \(t=1\), la recta tangente es

\[ \frac{x-1}{1} = \frac{y-1}{2} \Rightarrow y-1 = 2(x-1) \Rightarrow y = 2x-1, \]

y la recta normal es

\[ \frac{x-1}{2} = \frac{y-1}{-1} \Rightarrow y-1 = \frac{-1}{2}(x-1) \Rightarrow y = \frac{-x}{2}+\frac{3}{2}. \]

7.9.4 Recta tangente a una trayectoria en el espacio

El concepto de recta tangente a una trayectoria en el plano real puede extenderse fácilmente a trayectorias en el espacio real \(\mathbb{R}^3\).

Si \(f(t)=(x(t),y(t),z(t))\), \(t\in I\subseteq \mathbb{R}\), es una trayectoria en el espacio real \(\mathbb{R}^3\), entonces el móvil que recorre esta trayectoria en el instante \(t=t_0\), ocupará la posición \(P=(x(t_0),y(t_0),z(t_0))\) y tendrá una velocidad \(\mathbf{v}=f'(t)=(x'(t),y'(t),z'(t))\), de manera que la recta tangente a \(f\) en ese instante será

\[\begin{align*} l&: (x,y,z)=(x(t_0),y(t_0),z(t_0))+t(x'(t_0),y'(t_0),z'(t_0)) =\\ &= (x(t_0)+tx'(t_0),y(t_0)+ty'(t_0),z(t_0)+tz'(t_0)), \end{align*}\]

cuyas ecuaciones cartesianas son

\[ \frac{x-x(t_0)}{x'(t_0)}=\frac{y-y(t_0)}{y'(t_0)}=\frac{z-z(t_0)}{z'(t_0)}, \]

siempre que \(x'(t_0)\neq 0\), \(y'(t_0)\neq 0\) y \(z'(t_0)\neq 0\).

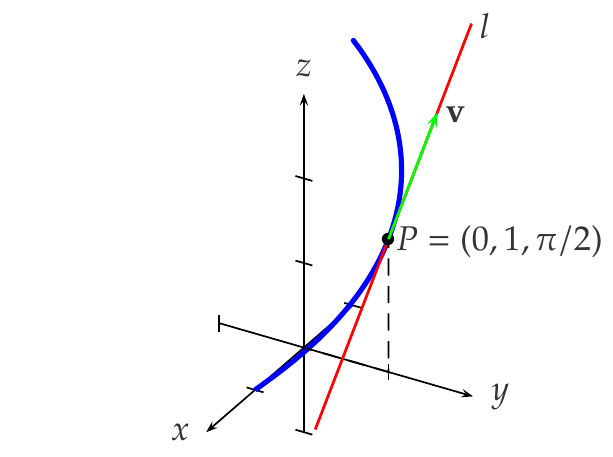
Ejemplo 7.28 Dada la trayectoria del espacio \(f(t)=(\cos(t), \operatorname{sen}(t), t)\), \(t\in \mathbb{R}\), en el instante \(t=\pi/2\), la trayectoria pasará por el punto

\[ f(\pi/2)=(\cos(\pi/2),\operatorname{sen}(\pi/2),\pi/2)=(0,1,\pi/2), \]

con una velocidad

\[ \mathbf{v}=f'(\pi/2)=(-\operatorname{sen}(\pi/2),\cos(\pi/2), 1)=(-1,0,1), \]

y la tangente en ese punto es

\[ l:(x,y,z)=(0,1,\pi/2)+t(-1,0,1) = (-t,1,t+\pi/2). \]

Gráfica de la tangente a una trayectoria en el espacio.

Ejemplo interactivo

7.10 Polinomios de Taylor

7.10.1 Aproximación de una función mediante un polinomio

Una aplicación muy útil de la derivada es la aproximación de funciones mediante polinomios.

Los polinomios son funciones sencillas de calcular (mediante sumas y productos), que tienen muy buenas propiedades:

  • Están definidos en todos los números reales.
  • Son funciones continuas.
  • Son derivables hasta cualquier orden y sus derivadas son continuas.

En esta sección veremos cómo aproximar una función \(f(x)\) mediante un polinomio \(p(x)\) cerca de un valor \(x=a\).

7.10.1.1 Aproximación mediante un polinomio de grado 0

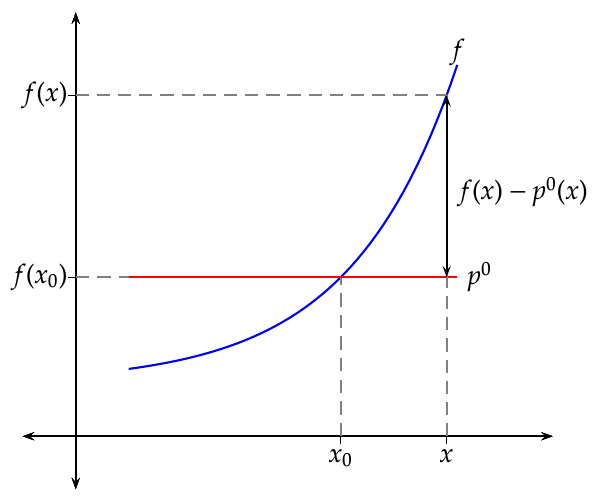
Un polinomio de grado 0 tiene ecuación \[p(x) = c_0,\] donde \(c_0\) es una constante.

Como el polinomio debe valer lo que la función en el punto \(a\), debe cumplir

\[ p(a) = c_0 = f(a). \]

En consecuencia, el polinomio de grado 0 que mejor aproxima a \(f\) en un entorno de \(a\) es

\[ p(x) = f(a). \]

Gráfica del polinomio de Taylor de grado 0

7.10.1.2 Aproximación mediante un polinomio de grado 1

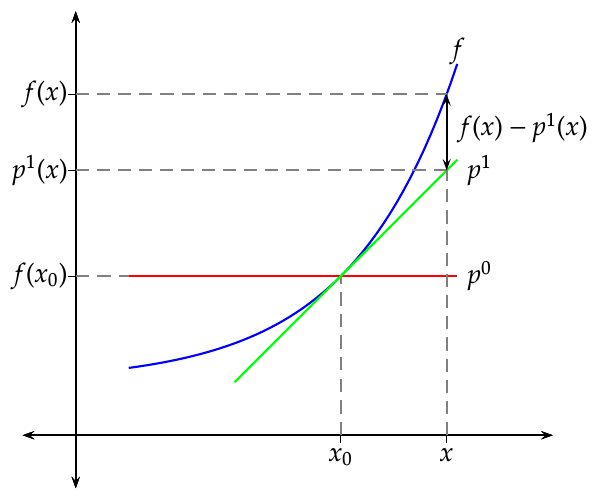
Un polinomio de grado 1 es una recta y tiene ecuación

\[ p(x) = c_0+c_1x, \]

aunque también puede escribirse

\[ p(x) = c_0+c_1(x-a). \]

De entre todos los polinomios de grado 1, el que mejor aproxima a \(f\) en entorno de \(a\) será el que cumpla las dos condiciones siguientes:

  • \(p\) y \(f\) valen lo mismo en \(a\): \(p(a) = f(a)\),
  • \(p\) y \(f\) tienen la misma tasa de crecimiento en \(a\): \(p'(a) = f'(a)\).

Esta última condición nos asegura que en un entorno de \(a\), \(p\) y \(f\) tienen aproximadamente la misma tendencia de crecimiento, pero requiere que la función \(f\) sea derivable en \(a\).

Imponiendo las condiciones anteriores tenemos

  • \(p(x)=c_0+c_1(x-a) \Rightarrow p(a)=c_0+c_1(a-a)=c_0=f(a)\),
  • \(p'(x)=c_1 \Rightarrow p'(a)=c_1=f'(a)\).

Así pues, el polinomio de grado 1 que mejor aproxima a \(f\) en un entorno de \(a\) es

\[ p(x) = f(a)+f '(a)(x-a), \]

que resulta ser la recta tangente a \(f\) en el punto \((a,f(a))\).

Gráfica del polinomio de Taylor de grado 1

7.10.1.3 Aproximación mediante un polinomio de grado 2

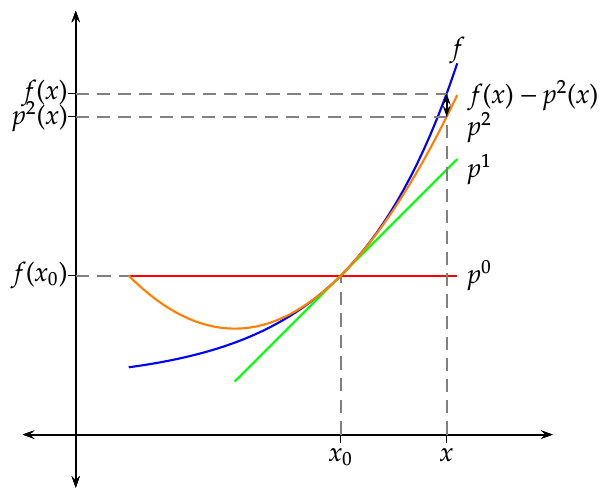
Un polinomio de grado 2 es una parábola y tiene ecuación

\[ p(x) = c_0+c_1x+c_2x^2, \]

aunque también puede escribirse

\[ p(x) = c_0+c_1(x-a)+c_2(x-a)^2. \]

De entre todos los polinomio de grado 2, el que mejor aproxima a \(f\) en entorno de \(a\) será el que cumpla las tres condiciones siguientes:

  • \(p\) y \(f\) valen lo mismo en \(a\): \(p(a) = f(a)\),
  • \(p\) y \(f\) tienen la misma tasa de crecimiento en \(a\): \(p'(a) = f'(a)\).
  • \(p\) y \(f\) tienen la misma curvatura en \(a\): \(p''(a)=f''(a)\).

Esta última condición requiere que la función \(f\) sea dos veces derivable en \(a\).

Imponiendo las condiciones anteriores tenemos

  • \(p(x)=c_0+c_1(x-a)+c_2(x-a)^2 \Rightarrow p(a)=c_0=f(a)\),
  • \(p'(x)=c_1+2c_2(x-a) \Rightarrow p'(a)=c_1+2c_2(a-a)=c_1=f'(a)\),
  • \(p''(x)=2c_2 \Rightarrow p''(a)=2c_2=f''(a) \Rightarrow c_2=\frac{f''(a)}{2}\).

Así pues, el polinomio de grado 2 que mejor aproxima a \(f\) en un entorno de \(a\) es

\[ p(x) = f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2. \]

Gráfica del polinomio de Taylor de grado 2

7.10.1.4 Aproximación mediante un polinomio de grado \(n\)

Un polinomio de grado \(n\) tiene ecuación

\[ p(x) = c_0+c_1x+c_2x^2+\cdots +c_nx^n, \]

aunque también puede escribirse

\[ p(x) = c_0+c_1(x-a)+c_2(x-a)^2+\cdots +c_n(x-a)^n. \]

De entre todos los polinomio de grado \(n\), el que mejor aproxima a \(f\) en entorno de \(a\) será el que cumpla las \(n+1\) condiciones siguientes:

  • \(p(a) = f(a)\),
  • \(p'(a) = f'(a)\),
  • \(p''(a)=f''(a)\),
  • \(\cdots\)
  • \(p^{(n}(a)=f^{(n}(a)\).

Las sucesivas derivadas de \(p\) valen

\[\begin{align*} p(x) &= c_0+c_1(x-a)+c_2(x-a)^2+\cdots +c_n(x-a)^n,\\ p'(x) &= c_1+2c_2(x-a)+\cdots +nc_n(x-a)^{n-1},\\ p''(x) &= 2c_2+\cdots +n(n-1)c_n(x-a)^{n-2},\\ \vdots\\ p^{(n}(x) &= n(n-1)(n-2)\cdots 1c_n = n!c_n. \end{align*}\]

Imponiendo las condiciones anteriores se tiene

  • \(p(a) = c_0+c_1(a-a)+c_2(a-a)^2+\cdots +c_n(a-a)^n=c_0=f(a),\)
  • \(p'(a) = c_1+2c_2(a-a)+\cdots +nc_n(a-a)^{n-1}=c_1=f'(a),\)
  • \(p''(a) = 2c_2+\cdots +n(n-1)c_n(a-a)^{n-2}=2c_2=f''(a)\Rightarrow c_2=\frac{f''(a)}{2},\)
  • \(\cdots\)
  • \(p^{(n}(a)=n!c_n=f^{(n}(a)=c_n=\frac{f^{(n}(a)}{n!}\).

Definición 7.11 (Polinomio de Taylor de orden \(n\) para \(f\) en el punto \(a\)) Dada una función \(f\), \(n\) veces derivable en \(x=a\), se define el polinomio de Taylor de orden \(n\) para \(f\) en \(a\) como

\[\begin{align*} p_{f,a}^n(x)&=f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\cdots +\frac{f^{(n}(a)}{n!}(x-a)^n = \\ &=\sum_{i=0}^{n}\frac{f^{(i}(a)}{i!}(x-a)^i, \end{align*}\]

o bien, escribiendo \(x=a+h\)

\[\begin{align*} p_f^n(a+h) &= f(a)+f'(a)h+\frac{f''(a)}{2}h^2+\cdots +\frac{f^{(n}(a)}{n!}h^n =\\ &= \sum_{i=0}^{n}\frac{f^{(i}(a)}{i!}h^i. \end{align*}\]

Importante

El polinomio de Taylor de orden \(n\) para \(f\) en \(a\) es el polinomio de orden \(n\) que mejor aproxima a \(f\) alrededor de \(a\), ya que es el único que cumple las \(n+1\) condiciones anteriores.

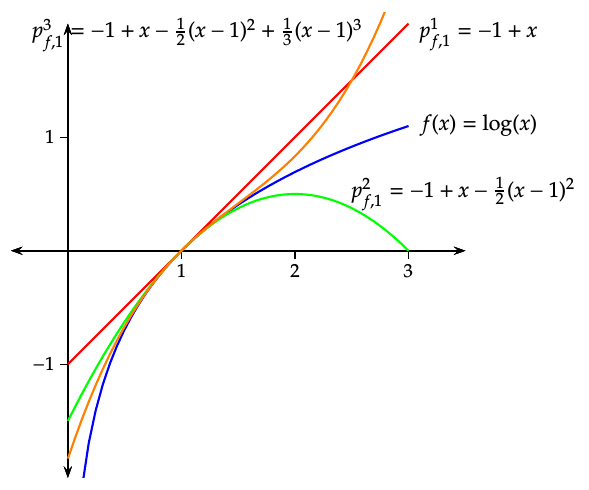
Ejemplo 7.29 Vamos a aproximar la función \(f(x)=\log x\) en un entorno del punto \(1\) mediante un polinomio de grado \(3\).

La ecuación del polinomio de Taylor de orden \(3\) para \(f\) en el punto \(1\) es

\[ p_{f,1}^3(x)=f(1)+f'(1)(x-1)+\frac{f''(1)}{2}(x-1)^2+\frac{f'''(1)}{3!}(x-1)^3. \]

Calculamos las tres primeras derivadas de \(f\) en \(1\):

\[ \begin{array}{lll} f(x)=\log x & \quad & f(1)=\log 1 =0,\\ f'(x)=1/x & & f'(1)=1/1=1,\\ f''(x)=-1/x^2 & & f''(1)=-1/1^2=-1,\\ f'''(x)=2/x^3 & & f'''(1)=2/1^3=2. \end{array} \]

Sustituyendo en la ecuación del polinomio se tiene

\[ p_{f,1}^3(x)=0+1(x-1)+\frac{-1}{2}(x-1)^2+\frac{2}{3!}(x-1)^3= \frac{2}{3}x^3-\frac{3}{2}x^2+3x-\frac{11}{6}. \]

Gráfica del polinomio de Taylor del logaritmo

7.10.2 Polinomio de Maclaurin de orden \(n\)

La ecuación del polinomio de Taylor se simplifica cuando el punto en torno al cual queremos aproximar es el \(0\).

Definición 7.12 (Polinomio de Maclaurin de orden \(n\) para \(f\)) Dada una función \(f\), \(n\) veces derivable en \(0\), se define el polinomio de Maclaurin de orden \(n\) para \(f\) como

\[\begin{align*} p_{f,0}^n(x) &= f(0)+f'(0)x+\frac{f''(0)}{2}x^2+\cdots +\frac{f^{(n}(0)}{n!}x^n =\\ &= \sum_{i=0}^{n}\frac{f^{(i}(0)}{i!}x^i. \end{align*}\]

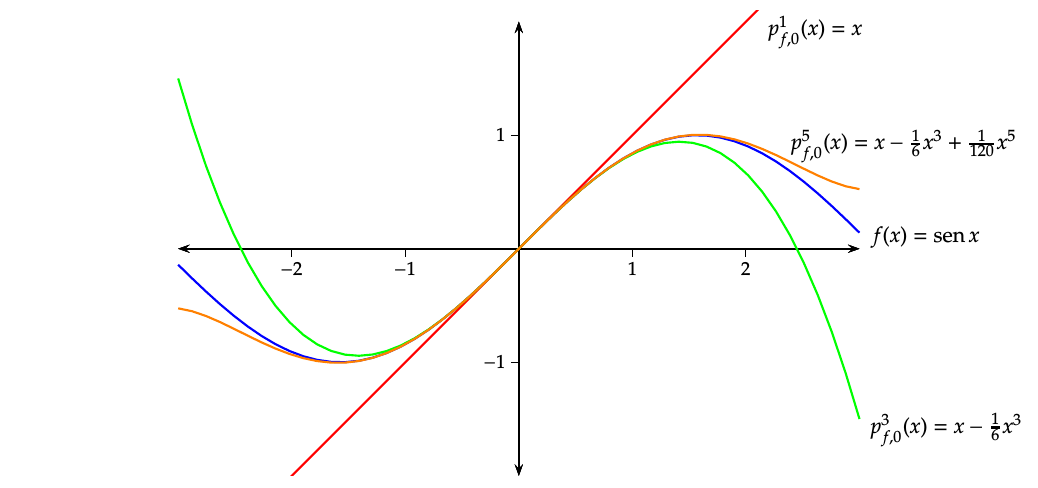
Ejemplo 7.30 Vamos a aproximar la función \(f(x)=\operatorname{sen} x\) en un entorno del punto \(0\) mediante un polinomio de grado \(3\).

La ecuación del polinomio de Maclaurin de orden \(3\) para \(f\) es

\[ p_{f,0}^3(x)=f(0)+f'(0)x+\frac{f''(0)}{2}x^2+\frac{f'''(0)}{3!}x^3. \]

Calculamos las tres primeras derivadas de \(f\) en \(0\):

\[ \begin{array}{lll} f(x)=\operatorname{sen} x & \quad & f(0)=\operatorname{sen} 0 =0,\\ f'(x)=\cos x & & f'(0)=\cos 0=1,\\ f''(x)=-\operatorname{sen} x & & f''(0)=-\operatorname{sen} 0=0,\\ f'''(x)=-\cos x & & f'''(0)=-\cos 0=-1. \end{array} \]

Sustituyendo en la ecuación del polinomio obtenemos

\[ p_{f,0}^3(x)=0+1\cdot x+\frac{0}{2}x^2+\frac{-1}{3!}x^3= x-\frac{x^3}{6}. \]

Gráfica del polinomio de Maclaurin del seno

7.10.3 Polinomios de Maclaurin de funciones elementales

La siguiente tabla recoge los polinomios de Taylor de orden \(n\) de algunas funciones elementales habituales.

\(f(x)\) \(p_{f,0}^n(x)\)
\(e^x\) \(\displaystyle 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!} = \sum_{i=0}^n \frac{x^i}{i!}\)
\(\log(1+x)\) \(\displaystyle x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots +(-1)^{n-1}\frac{x^n}{n} = \sum_{i=0}^n (-1)^{i-1}\frac{x^i}{i}\)
\(\operatorname{sen}(x)\) \(\displaystyle x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots +(-1)^k\frac{x^{2k-1}}{(2k-1)!} = \sum_{i=0}^k (-1)^i\frac{x^{2i-1}}{(2i-1)!}\) si \(n=2k\) o \(n=2k-1\)
\(\cos(x)\) \(\displaystyle 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots +(-1)^k\frac{x^{2k}}{(2k)!} = \sum_{i=0}^k (-1)^i\frac{x^{2i}}{(2i)!}\) si \(n=2k\) o \(n=2k+1\)
\(\operatorname{arctg}(x)\) \(\displaystyle x-\frac{x^3}{3}+\frac{x^5}{5}-\cdots +(-1)^k\frac{x^{2k-1}}{(2k-1)} = \sum_{i=0}^k (-1)^i\frac{x^{2i-1}}{(2i-1)}\) si \(n=2k\) o \(n=2k-1\)

7.10.4 Resto de Taylor

Los polinomios de Taylor permiten calcular el valor aproximado de una función cerca de un valor \(a\), pero siempre se comete un error en dicha aproximación.

Definición 7.13 (Resto de Taylor) Si \(f\) es una función para la que existe el su polinomio de Taylor de orden \(n\) en \(a\), \(p_{f,a}^n\), entonces se define el resto de Taylor de orden \(n\) para \(f\) en \(a\) como

\[ r_{f,a}^n(x)=f(x)-p_{f,a}^n(x). \]

El resto mide el error cometido al aproximar \(f(x)\) mediante \(p_{f,a}^n(x)\) y permite expresar la función \(f\) como la suma de un polinomio de Taylor más su resto correspondiente:

\[ f(x)=p_{f,a}^n(x) + r_{f,a}^n(x). \]

Esta expresión se conoce como fórmula de Taylor de orden \(n\) para \(f\) en \(a\). Se pude demostrar, además, que

\[ \lim_{h\rightarrow 0}\frac{r_{f,a}^n(a+h)}{h^n}=0, \]

lo cual indica que el resto \(r_{f,a}^n(a+h)\) es mucho menor que \(h^n\).

Teorema 7.11 (Forma de Lagrange del resto de Taylor) Si \(f\) es una función tal que \(f^{(n+1}(t)\) es continua en un intervalo que incluye a \(a\) y \(x\), entonces

\[ R^n_{f,a}(x)=\frac{f^{(n+1}(c)}{(n+1)!}(x-a)^{n+1} \]

para algún \(c\) entre \(a\) y \(x\).

La forma de Lagrange del resto de Taylor permite, en muchas ocasiones, dar una cota de las aproximaciones realizadas mediante un polinomio de Taylor.

Ejemplo 7.31 Dada la función \(f(x)=\cos(x)\) el polinomio de MacLaurin de cuarto grado de \(f\) es

\[ P^4_{f,0}(x)=1-\frac{x^2}{2}+\frac{x^4}{4!}. \]

Sustituyendo en \(x=0.1\) se tiene que \(\cos(0.1)\approx P^2_{f,0}(0.1) = 1-\frac{0.1^2}{2}+\frac{0.1^4}{4!}= 0.9950041667\).

Para obtener una cota del error cometido, aplicando el teorema anterior se tiene que

\[ R^4_{f,0}(0.1)=\frac{f^{5}(c)}{5!}0.1^5 = \frac{-\operatorname{sen}(c)}{5!}0.1^5 \mbox{ con }c\in [0,0.1]. \]

Como \(|\operatorname{sen}(x)|\leq 1\) \(\forall x\in\mathbb{R}\), se tiene que

\[ |R^4_{f,0}(0.1)|\leq \frac{0.1^5}{5!} = 8.3\cdot 10^{-8}, \]

que es una cota del error cometido en la aproximación.