5  Derivadas de funciones reales

5.1 Ejercicios Resueltos

Para la realización de esta práctica se requieren los siguientes paquetes:

using SymPy  # Para el cálculo simbólico de límites.
using Plots  # Para el dibujo de gráficas.
#plotlyjs() # Para obtener gráficos interactivos.
using ImplicitPlots # Para dibujar curvas implícitas.
using MTH229 # Para restringir la gráfica de una función a su dominio.
using LaTeXStrings  # Para usar código LaTeX en los gráficos.
using Latexify  # Para convertir expresiones a código LaTeX.

Ejercicio 5.1 Galileo Galilei trató de estudiar el movimiento de un cuerpo en caída libre con un experimento en el que midió la distancia recorrida cada segundo por una bola que caía por un plano inclinado.

Plano inclinado de Galileo.

La siguiente tabla recoge sus mediciones.

Tiempo (s)	Distancia (cm)
0	0
1	1
2	4
3	9
4	16
5	25

1. Dibujar la gráfica que resulta de unir los puntos correspondientes a los pares de la tabla con segmentos. ¿Qué forma tiene la gráfica?

   Ayuda

   Definir dos arrays con los valores del tiempo y la distancia y usar la función scatter del paquete Plots, o bien la función scatter del paquete Makie, para dibujar el array de términos.

   Solución

   Plots

   using Plots
   t = [0, 1, 2, 3, 4, 5, 6]
   d = [0, 1, 4, 9, 16, 25, 36]
   Plots.scatter(t, d, legend=false)
   plt = Plots.plot!(t, d, linecolor="blue", xlab="Tiempo (s)", ylab="Distancia recorrida (cm)")

   Makie

   using GLMakie
   t = [0, 1, 2, 3, 4, 5, 6]
   d = [0, 1, 4, 9, 16, 25, 36]
   fig = Figure()
   ax = Axis(fig[1,1], xlabel="Tiempo (s)", ylabel="Distancia recorrida (cm)")
   Makie.scatter!(ax, t, d)
   f(x) = x^2
   Makie.lines!(ax, 0..6, f)
   fig

   

   Se aprecia que una forma parabólica.

2. Calcular la velocidad media (tasa de variación media) desde los instantes $t=0,1,2$ hasta el instante $t=3$ y dibujar la rectas secantes a la gráfica anterior en esos instantes. ¿Cómo es la tendencia de las velocidades medias?

   Ayuda

   La tasa de variación media de una función $f$ en un intervalo $[a,b]$ viene dada por la fórmula

   $$TVM(f,[a,b])=\frac{f(b)-f(a)}{b-a},$$

   y la recta secante a la función $f$ en el intervalo $[a,b]$ tiene ecuación

   $$y=f(a)+TVM(f,[a,b])(x-a).$$

   Solución

   # Función para el cálculo de la velocidad media en del instante i al instante j.
   tvm(i, j) = (d[j]-d[i])/(t[j]-t[i])
   j = 4
   # Cálculo de las velocidades medias.
   for i in 1:3
       println("Velocidad media desde el instante $(t[i]) al instante $(t[j]): $(tvm(i, j)) cm/s")
   end
   # Función para calcular la ecuación de la recta secante en los instantes i y j.
   secante(x, i, j) = d[i] + tvm(i, j) * (x - t[i])
   # Dibujo de las rectas secantes
   for i in 1:3
       plt = Plots.plot!(x -> secante(x,i,j))
   end
   plt

   Velocidad media desde el instante 0 al instante 3: 3.0 cm/s
   Velocidad media desde el instante 1 al instante 3: 4.0 cm/s
   Velocidad media desde el instante 2 al instante 3: 5.0 cm/s

   Las velocidades medias crecen a medida que pasa el tiempo.

3. Calcular la velocidad media desde el instante $t=3$ hasta los instantes $t=6,5,4$ y dibujar la rectas secantes a la gráfica anterior en esos instantes. ¿Cómo es la tendencia de las velocidades medias? ¿Hacia dónde tiende la velocidad media cuando los aproximamos al instante $t=3$ con instantes menores y mayores?

   Solución

   i = 4
   # Cálculo de las velocidades medias.
   for j in 7:-1:5
       println("Velocidad media desde el instante $(t[i]) al instante $(t[j]): $(tvm(i, j)) cm/s")
   end
   # Dibujo de las rectas secantes.
   for j in 7:-1:5
       plt = Plots.plot!(x -> secante(x,i,j))
   end
   plt

   Velocidad media desde el instante 3 al instante 6: 9.0 cm/s
   Velocidad media desde el instante 3 al instante 5: 8.0 cm/s
   Velocidad media desde el instante 3 al instante 4: 7.0 cm/s

   Las velocidades medias decrecen a medida que el tiempo decrece.

   Se puede deducir que las velocidades medias tienden a $6$ cm/s cuando los instantes se aproximan a $3$ s.

4. Calcular la variación en la distancia recorrida cada segundo que pasa. ¿Cómo evoluciona la velocidad de la bola?

   Solución

   v = []
   for i in 2:length(d)
       push!(v, d[i]-d[i-1])
       println("Velocidad media desde el instante $(t[i-1]) al instante $(t[i]): $(v[i-1]) cm/s")
   end

   Velocidad media desde el instante 0 al instante 1: 1 cm/s
   Velocidad media desde el instante 1 al instante 2: 3 cm/s
   Velocidad media desde el instante 2 al instante 3: 5 cm/s
   Velocidad media desde el instante 3 al instante 4: 7 cm/s
   Velocidad media desde el instante 4 al instante 5: 9 cm/s
   Velocidad media desde el instante 5 al instante 6: 11 cm/s

5. Calcular la variación en la velocidad cada segundo que pasa. ¿Cómo evoluciona la aceleración de la bola? ¿Qué conclusiones sacó Galileo sobre la aceleración de la bola?

   Solución

   for i in 2:length(v)
       println("Aceleración media desde el instante $(t[i-1]) al instante $(t[i]): $(v[i]-v[i-1]) cm/s")
   end

   Aceleración media desde el instante 0 al instante 1: 2 cm/s
   Aceleración media desde el instante 1 al instante 2: 2 cm/s
   Aceleración media desde el instante 2 al instante 3: 2 cm/s
   Aceleración media desde el instante 3 al instante 4: 2 cm/s
   Aceleración media desde el instante 4 al instante 5: 2 cm/s

   Se observa que la aceleración es la misma. Galileo concluyó que la aceleración de un cuerpo en caída libre era uniforme.

Ejercicio 5.2 Representar gráficamente la función $f(x)=|x-1|$ y estudiar su derivabilidad en el punto $x=1$ haciendo uso de la definición de derivada.

Solución

using Plots, SymPy, LaTeXStrings
@syms x::real
f(x) = abs(x-1)
display(Plots.plot(f(x), label=L"f(x)=|x-1|"))
println("Derivada por la izquierda: ", limit((f(x)-f(1))/(x-1), x=>1, dir="-"))
println("Derivada por la derecha: ", limit((f(x)-f(1))/(x-1), x=>1, dir="+"))

Derivada por la izquierda: -1
Derivada por la derecha: 1

Como la derivada por la izquierda y por la derecha no son iguales, la función no es derivable en $x=1$.

Ejercicio 5.3 Calcular las derivadas de las siguientes funciones hasta el orden 4 y deducir la expresión de la derivada de orden $n$.

1. $f(x)=\ln (x+1)$

   Ayuda

   Usar la función diff(f,n) del paquete SymPy para calcular simbólicamente la derivada de grado n de la función f.

   Solución

   using SymPy
   @syms x::real
   f(x) = log(x+1)
   println("Primera derivada: ", diff(f(x)))
   println("Segunda derivada: ", diff(f(x), x, 2))
   println("Tercera derivada: ", diff(f(x), x, 3))
   println("Cuarta derivada: ", diff(f(x), x, 4))

   Primera derivada: 1/(x + 1)
   Segunda derivada: -1/(x + 1)^2
   Tercera derivada: 2/(x + 1)^3
   Cuarta derivada: -6/(x + 1)^4

   La derivada de orden $n$ es $f^{(n}=\frac{(-1{)}^{n-1}(n-1)!}{(x+1{)}^n}$.

2. $f(x)=a^x$

   Solución

   using SymPy
   @syms x::real a::real
   g(x) = a^x
   println("Primera derivada: ", diff(g(x), x))
   println("Segunda derivada: ", diff(g(x), x, 2))
   println("Tercera derivada: ", diff(g(x), x, 3))
   println("Cuarta derivada: ", diff(g(x), x, 4))

   Primera derivada: a^x*log(a)
   Segunda derivada: a^x*log(a)^2
   Tercera derivada: a^x*log(a)^3
   Cuarta derivada: a^x*log(a)^4

   La derivada de orden $n$ es $g^{(n}=a^x\ln (a{)}^n$.

3. $h(x)=\mathrm{sen}(x)+\cos (x)$

   Solución

   using SymPy
   @syms x::real
   h(x) = sin(x)+cos(x)
   println("Primera derivada: ", diff(h(x)))
   println("Segunda derivada: ", diff(h(x), x, 2))
   println("Tercera derivada: ", diff(h(x), x, 3))
   println("Cuarta derivada: ", diff(h(x), x, 4))

   Primera derivada: -sin(x) + cos(x)
   Segunda derivada: -(sin(x) + cos(x))
   Tercera derivada: sin(x) - cos(x)
   Cuarta derivada: sin(x) + cos(x)

   La derivada de orden $n$ es

   $$h^{(n}=\{\begin{array}{ll}\mathrm{sen}(x)+\cos (x)& \text{si }n=4k\\ \cos (x)-\mathrm{sen}(x)& \text{si }n=4k+1\\ -\mathrm{sen}(x)-\cos (x)& \text{si }n=4k+2\\ -\cos (x)+\mathrm{sen}(x)& \text{si }n=4k+3\end{array}k\in \mathbb{N}$$

Ejercicio 5.4 Sea $f(x)=\sqrt{x}$.

1. Dibujar la gráfica de $f$ y dibujar las rectas secantes a $f$ en los intervalos $[\frac{i}{10},1]$ para $i=0,\dots ,9$. ¿Hacia dónde tienden las pendientes de las rectas secantes?

   Solución

   using Plots, SymPy, LaTeXStrings, Latexify
   @syms x::real
   f(x) = sqrt(x)
   plt = Plots.plot(f, 0, 2, ylims=(0,2.5), linewidth = 3, label=L"f(x)=\sqrt{x}", legend=:topleft)
   secante(x, i, j) = f(i) + (f(j)-f(i))/(j-i) * (x - i)
   for i in 0:9
       sec = secante(x, i/10, 1)
       plt = Plots.plot!(sec, label =L"y=" * latexify(sec))
   end
   plt

   Se deduce que las pendientes de las rectas secantes tienen a $0.5$.

2. Dibujar la recta tangente a la gráfica de $f$ en $x=1$.

   Ayuda

   La ecuación de la recta tangente a la función $f(x)$ en el punto $a$ es $y=f(a)+f^{\prime }(a)(x-a)$.

   Usar la función diff(f) del paquete SymPy para calcular simbólicamente la derivada de la función f.

   Solución

   tg = f(1) + diff(f(x))(1) * (x-1)
   Plots.plot!(tg, linewidth = 2, color = "red", label="Tangente " * L"y=" * latexify(tg))

Ejercicio 5.5 Calcular y dibujar las rectas tangente y normal a la gráfica de la función $f(x)=\ln (\sqrt{x+1})$ en $x=1$.

Ayuda

La ecuación de la recta tangente a una función $f$ en el punto $a$ es

$$y=f(a)+f^{\prime }(a)(x-a),$$

y la de la recta normal

$$y=f(a)-\frac{1}{f^{\prime }(a)}(x-a).$$

Solución

using Plots, SymPy, LaTeXStrings, Latexify
@syms x::real
f(x) = log(sqrt(x+1))
Plots.plot(f, -1, 3, xlims=(-1,3), ylims=(-1,2), aspect_ratio=1, label=L"f(x)=\ln(\sqrt{x+1})", legend=:topright)
tg = f(1) + diff(f(x))(1) * (x-1)
Plots.plot!(tg, label="Tangente "*L"y="*latexify(tg))
nm = f(1) - 1/diff(f(x))(1) * (x-1)
Plots.plot!(nm, label="Normal "*L"y="*latexify(nm))

Ejercicio 5.6 Sea la función $g(x)={\displaystyle \frac{2x^3-3x}{x^2+1}}$.

1. Dibujar la gráfica de $g$.

   Solución

   using Plots, SymPy, LaTeXStrings, Latexify
   @syms x::real
   g(x) = (2x^3-3x) / (x^2+1)
   Plots.plot(g, -2, 2, label=L"g(x)=\frac{2x^3-3x}{x^2+1}", legend=:topleft)

2. Calcular la derivada de $g$ y dibujar su gráfica en la misma gráfica que la de $g$.

   Solución

   Plots.plot!(diff(g(x)), label=L"g'(x)="*latexify(simplify(diff(g(x)))))

3. Calcular los puntos críticos de $g$.

   Ayuda

   Los puntos críticos de una función son los puntos donde se anula la derivada.

   Solución

   N.(solve(diff(g(x))))

   2-element Vector{Float64}:
    -0.5583347485961263
     0.5583347485961263

   Existen dos puntos críticos en $x=-0.55$ y $x=0.55$ aproximadamente.

4. A la vista de los puntos críticos y de la gráfica de la función derivada, determinar los intervalos de crecimiento y los extremos relativos de la función.

   Ayuda

   Una función $f$ derivable en el punto $a$ es creciente si y solo si $f^{\prime }(a)>0$ y decrecientes si y solo si $f^{\prime }(a)<0$.

   Solución

   La derivada es positiva en los intervalos $(-\mathrm{\infty },-0.55)$ y $(0.55,\mathrm{\infty })$, por lo que la función $g$ es creciente en estos intervalos, y la derivada es negativa en el intervalo $(-0.55,0.55)$, por lo que la función $g$ es decreciente en este intervalo.

   En el punto crítico $x=-0.55$ la derivada es positiva a la izquierda y negativa a la derecha, por lo que, según el criterio de la primera derivada, la función $g$ tiene un máximo relativo.

   En el punto crítico $x=0.55$ la derivada es negativa a la izquierda y positiva a la derecha, por lo que, según el criterio de la primera derivada, la función $g$ tiene un mínimo relativo.

5. Calcular segunda la derivada de $g$ y dibujar su gráfica en la misma gráfica que la de $g$.

   Solución

   Plots.plot!(diff(g(x), x, 2), label=L"g''(x)="*latexify(simplify(diff(g(x), x, 2))))

6. Calcular los puntos que anulan la segunda derivada de $g$.

   Solución

   N.(solve(diff(g(x), x, 2)))

   3-element Vector{Real}:
     0
    -1.7320508075688772
     1.7320508075688772

   Existen tres puntos donde se anula $g^{″}(x)$, en $x=-1.73$, $x=0$ y $x=1.73$ aproximadamente.

7. A la vista de las raíces de la gráfica de la segunda derivada, determinar los intervalos de concavidad y los puntos de inflexión de la función $g$.

   Ayuda

   Una función $f$ dos veces derivable en el punto $a$ es cóncava hacia arriba si y solo si $f^{″}(a)>0$ y cóncava hacia abajo si y solo si $f^{″}(a)<0$. Los puntos de inflexión de una función son los puntos donde cambia la concavidad.

   Solución

   La segunda derivada es positiva en los intervalos $(-\mathrm{\infty },-1,73)$ y $(0,1.73)$, por lo que la función $g$ es cóncava hacia arriba en esos intervalos, y la segunda derivada es negativa en los intervalos $(-1.73,0)$ y $(1.73,\mathrm{\infty })$, por lo que la función $g$ es cóncava hacia abajo en esos intervalos.

   $g$ tiene tres puntos de inflexión en $x=1.73$, $x=0$ y $x=1.73$, donde cambia la concavidad de la función.

Ejercicio 5.7 Considérese la curva con ecuación $x^4-3x^2+2y^2=0$.

1. Dibujar la gráfica de la curva.

   Ayuda

   Para dibujar curvas implícitas utilizar la función implicit_plot del paquete ImplicitPlots.

   Solución

   using ImplicitPlots, Plots, SymPy, LaTeXStrings, Latexify
   @syms x::real y::real
   f(x,y) = x^4 - 3x^2 + 2y^2
   ImplicitPlots.implicit_plot(f; xlims=(-3,3), ylims=(-1.5,1.5), label=L"x^4-3x^2+2y^2=0", legend=:topleft)

2. Calcular la tasa de variación de $y$ con respecto a $x$ en el punto $(1,1)$.

   Ayuda

   Para realizar derivadas implícitas simbólicamente hay que definir una función simbólica con el comando @syms u() del paquete SymPy y reemplazar y por u(x) en la ecuación de la curva implícita.

   Después hay que hacer la derivada de ambos lados de la ecuación y finalmente hay que resolver la ecuación despejando la derivada de u(x).

   Solución

   # Declaramos una función simbólica.
   @syms u()
   # Reemplazamos y por una función implícita u(x) y calculamos la derivada implícitamente.
   df = diff(f(x, u(x)))
   # Resolvemos la ecuación para la derivada de u(x).
   du = solve(df, diff(u(x)))[1]
   # Deshacemos el cambio y = u(x).
   dy = du(u(x) => y)

   $\frac{x(3-2x^2)}{2y}$

3. Dibujar la recta tangente a la curva anterior en el punto $(1,1)$.

   Solución

   using Latexify
   # Definimos la función de la recta tangente
   tg = 1 + dy(1,1) * (x-1)
   Plots.plot!(tg, label="Tangente "*L"y="*latexify(tg))
   # Dibujamos el punto (1,1)
   Plots.scatter!([1],[1], label="")

Ejercicio 5.8 Crear una función para calcular el polinomio de Taylor de grado $n$ una función $f$ en un punto $a$ y utilizarla para dibujar los polinomios de Taylor de la función $f(x)=\mathrm{sen}(x)$ en $a=0$ hasta el grado $5$. Calcular y dibujar el error cometido al aproximar $\mathrm{sen}(\pi /6)$ mediante los polinomios de Taylor hasta el grado $1$ a $9$.

Ayuda

La fórmula del polinomio de Taylor de grado $n$ de la función $f$ en el punto $a$ es

$$P_{f,a}^n(x)=f(a)+f^{\prime }(a)(x-a)+\frac{f^{″}(a)}{2!}(x-a{)}^2+\cdots +\frac{f^{(n}(a)}{n!}(x-a{)}^n.$$

Solución

using Plots, SymPy, LaTeXStrings, Latexify
@syms x::real

function taylor(f, a=0, n=2)
    sum(diff(f, x, i)(a) / factorial(i) * (x-a)^i for i=0:n)
end

f(x) = sin(x)
plt = Plots.plot(f, ylims=(-2,2), linewidth=3, label=L"f(x)=\operatorname{sen}(x)")

for i in 1:5
    pol = taylor(f(x), 0, i)
    plt = Plots.plot!(pol, label=latexstring("P^{$(i)}(x)=$(pol)"))
end 
plt

Calculamos ahora los errores cometidos al aproximar $\mathrm{sen}(\pi /6)$ mediante los polinomios de Taylor hasta el grado $1$ a $9$.

errores = []
for i in 1:9
    pol = taylor(f(x), 0, i)
    push!(errores, abs(sin(pi/6)-pol(pi/6)))
end
errores

9-element Vector{Any}:
   0.0235987755982989
   0.0235987755982989
 0.000325820605636185
 0.000325820605636185
  2.13258879250278e-6
  2.13258879250278e-6
  8.13097672525132e-9
  8.13097672525132e-9
 2.02799443904667e-11

Finalmente, dibujamos los errores cometidos.

Plots.scatter(1:9, errores, xlab="Grado", ylab="Error", legend=false)

Ejercicio 5.9 Calcular los polinomios de Taylor hasta grado 10 de las siguientes funciones en los puntos indicados.

1. $f(x)=\cos (x)$ en $x=\pi /2$.

   Ayuda

   Para calcular polinomios de Taylor utilizar la función series del paquete SymPy.

   Advertencia

   La función series da el polinomio de grado $n-1$ junto con el error de orden $n$, por lo que si se quiere un polinomio de orden $n$ hay que llamar a la función con un orden $n+1$.

   Solución

   using SymPy
   @syms x::real
   f(x) = cos(x)
   SymPy.series(f(x), x, PI/2, 11)

   $\frac{\pi }{2}+\frac{{(x-\frac{\pi }{2})}^3}{6}-\frac{{(x-\frac{\pi }{2})}^5}{120}+\frac{{(x-\frac{\pi }{2})}^7}{5040}-\frac{{(x-\frac{\pi }{2})}^9}{362880}-x+O({(x-\frac{\pi }{2})}^{11};x\to \frac{\pi }{2})$

2. $g(x)=\ln (x)$ en $x=1$

   Solución

   g(x) = log(x)
   SymPy.series(g(x), x, 1, 11)

   $-1-\frac{{(x-1)}^2}{2}+\frac{{(x-1)}^3}{3}-\frac{{(x-1)}^4}{4}+\frac{{(x-1)}^5}{5}-\frac{{(x-1)}^6}{6}+\frac{{(x-1)}^7}{7}-\frac{{(x-1)}^8}{8}+\frac{{(x-1)}^9}{9}-\frac{{(x-1)}^{10}}{10}+x+O({(x-1)}^{11};x\to 1)$

   1. $h(x)=e^{\mathrm{sen}(x)}$ en $x=0$
   Solución

   h(x) = exp(sin(x))
   SymPy.series(h(x), x, 0, 11)

   $1+x+\frac{x^2}{2}-\frac{x^4}{8}-\frac{x^5}{15}-\frac{x^6}{240}+\frac{x^7}{90}+\frac{31x^8}{5760}+\frac{x^9}{5670}-\frac{2951x^{10}}{3628800}+O\left(x^{11}\right)$

Ejercicio 5.10 Aproximar el número $\ln (1.2)$ mediante un polinomio de Taylor de grado 8 y dar una cota del error cometido. ¿Hasta qué grado habría que llegar para obtener un error menor de ${10}^{-10}$?

Ayuda

El error en la aproximación de una función $f(b)$ mediante un polinomio de Taylor de grado $n$ en el punto $a$ viene dado por el resto de Taylor, que en la forma de Lagrange es

$$R_{f,a}^n(x)=\frac{f^{(n+1}(x)}{(n+1)!}(x-a{)}^{n+1}\text{ con }x\in [a,b].$$

Solución

Utilizaremos un polinomio de MacLaurin de grado 5 para la función $f(x)=\ln (1+x)$.

using SymPy
@syms x::real
f(x) = log(1+x)
pol = SymPy.series(f(x), x, 0, 6).removeO()
println("Aproximación de ln(1.2): ", N(pol(0.2)))

Aproximación de ln(1.2): 0.18233066666666667

Para dar una cota del error cometido calculamos el resto de Taylor en la forma de Lagrange.

resto = diff(f(x), x, 6) / factorial(6) * 0.2^6
println("Resto de Taylor de orden 6: ", resto)
println("Derivada del resto : ", diff(resto))

Resto de Taylor de orden 6: -1.06666666666667e-5/(x + 1)^6
Derivada del resto : 6.4e-5/(x + 1)^7

Como la derivada no se anula en el intervalo $[1,2]$, no hay extremos relativos, y al ser una función continua en un intervalo cerrado, alcanza el máximo y mínimos absolutos en los extremos.

println("Cota del error: " , maximum(N(abs.([resto(0), resto(0.2)])))) 
println("Error: ", abs(log(1.2)-pol(0.2)))

Cota del error: 1.06666666666667e-5
Error: 9.10987271207642e-6

Así pues, el error en la aproximación de $\ln (1.2)$ es menor que $1.06\cdot {10}^{-5}$.

Para ver la fórmula general del resto de Taylor en la forma de Lagrange para un polinomio de Taylor de orden $n$, calculamos las primeras derivadas sucesivas.

println("Primera derivada: ", diff(f(x)))
println("Segunda derivada: ", diff(f(x), x, 2))
println("Tercera derivada: ", diff(f(x), x, 3))
println("Cuarta derivada: ", diff(f(x), x, 4))

Primera derivada: 1/(x + 1)
Segunda derivada: -1/(x + 1)^2
Tercera derivada: 2/(x + 1)^3
Cuarta derivada: -6/(x + 1)^4

Así pues, se deduce que la derivada de orden $n$ es $f^{(n}(x)=(-1{)}^{n-1}\frac{(n-1)!}{(x+1{)}^n}$, de manera que el resto de Taylor de orden $n$ es

$$|R_{f,0}^n(x)|=|(-1{)}^{n-1}\frac{(n-1)!}{(n+1)!(x+1{)}^n}{0.2}^{n+1}|=\left|\frac{{0.2}^{n+1}}{(n+1)n(x+1{)}^n}\right|x\in [0,0.2].$$

Como se trata de una función positiva y decreciente en el intervalo $[0,0.2]$, alcanza el máximo absoluto en el extremo inferior del intervalo, es decir, en $x=0$, y por tanto se tiene,

$$|R_{f,1}^n(x)|\le \left|\frac{{0.2}^{n+1}}{(n+1)n}\right|.$$

Finalmente calculamos el primer número natural $n$ tal que $|R_{f,1}^n(x)|<{10}^{-10}$.

n=6
while 0.2^(n+1) / (n*(n+1)) > 10^-10
    n += 1
end
print(n)

11

Así pues, habría que llegar al grado 11.

5.2 Ejercicios propuestos

Ejercicio 5.11 Dada la función

$$f(x)=\{\begin{array}{ll}\mathrm{sen}(x{)}^2& \text{si }x\le 0,\\ a{x}^2+b& \text{si }0<x\le c,\\ \ln (x)& \text{si }c<x,\end{array}$$

¿Para qué valores de $a$, $b$ y $c$ la función es derivable en todo $\mathbb{R}$?

Select an item

$a=1,b=0,c=e.$

$a=1,b=1,c=1.$

$a=\sqrt{e},b=0,c=\frac{1}{e}.$

Para ningún valor.

$a=\frac{1}{2e},b=0,c=e^{1/2}.$

Ejercicio 5.12 ¿Cuál es la derivada de orden $n$ de la función $f(x)={\displaystyle \frac{1}{\sqrt{x+1}}}$?

Select an item

$\frac{(-1{)}^n\prod _{i=1}^{n}2i+1}{2^n}(x+1{)}^{-(2n+1)/2}.$

$\frac{(-1{)}^{n}n!}{2^n}(x+1{)}^{-n/2}.$

$\frac{(-1{)}^n(2n-1)!}{2^n}(x+1{)}^{-(2n-1)/2}.$

$\frac{(-1{)}^n\prod _{i=1}^{n}2i}{2^n}(x+1{)}^{-(2n+1)/2}.$

$\frac{(-1{)}^n\prod _{i=1}^{n}2i-1}{2^n}(x+1{)}^{-(2n+1)/2}.$

Ejercicio 5.13 Dadas las funciones $f(x)=\ln \left(\sqrt{{\displaystyle \frac{x^2}{2}}}\right)$ y $g(x)=x^3+1$, ¿en qué puntos la recta normal a $f$ y la recta tangente a $g$ con paralelas?

Ejercicio 5.14 Calcular el máximo y el mínimo absoluto de la función $g(x)=\sqrt{x^4-3x^3+\frac{5}{2}{x}^2}$ en el intervalo $[-0.5,1.5]$.

1. Mínimo absoluto

   
   

2. Máximo absoluto

   
   

Ejercicio 5.15 ¿Cuáles de las siguientes afirmaciones son ciertas sobre la función $h(x)={\displaystyle \frac{x^2+1}{e^x}}$?

Es cóncava hacia abajo en $(1,3)$.

Tiene un punto de inflexión en $x=3$.

Tiene un máximo en $x=1$.

Es decreciente en todo $\mathbb{R}$.

Tiene un mínimo en $x=1$.

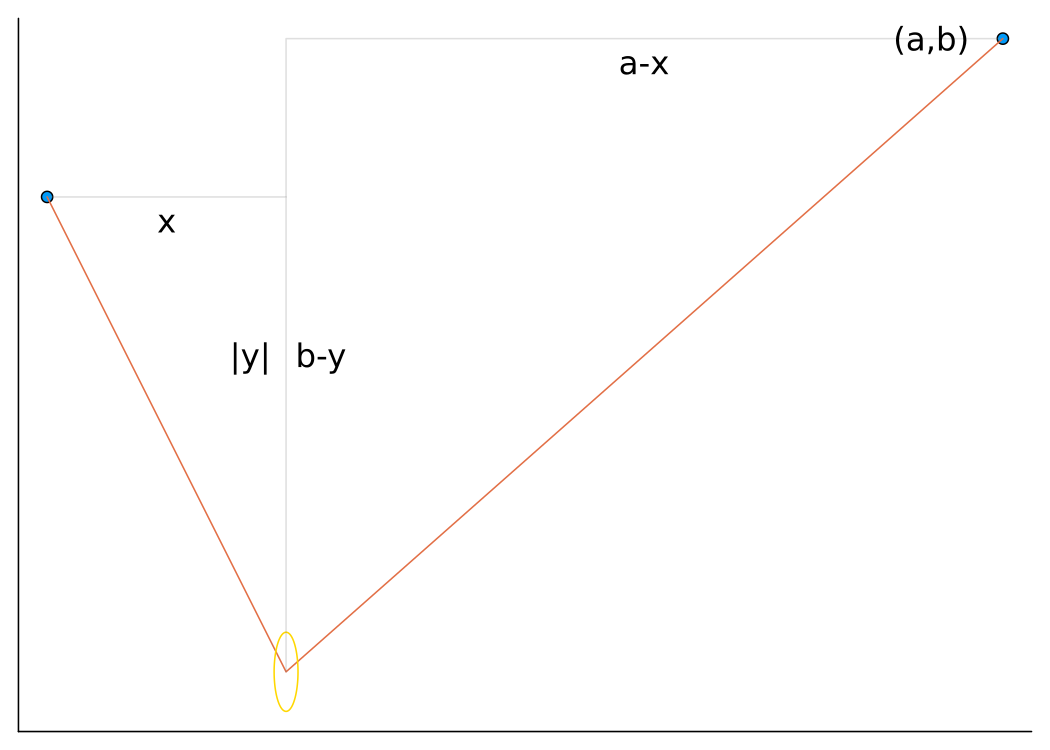
Ejercicio 5.16 Una cuerda de longitud $l$ está sujeta en sus extremos en los puntos $(0,0)$ y $(a,b)$. De la cuerda cuelga un anillo. ¿En qué posición estará el anillo debido a la fuerza de gravedad suponiendo que $l=10$, $a=3$ y $b=2$?

Ayuda

Puesto que la longitud de la cuerda es fija, del siguiente diagrama se deduce que las las posiciones $(x,y)$ que puede ocupar el anillo vienen dadas por la ecuación

$$l=\sqrt{x^2+y^2}+\sqrt{(a-x{)}^2+(b-y{)}^2}$$

Descomposición en triángulos rectángulos de la posición que ocupa un anillo suspendido de una cuerda de tamaño $l$ sujeta en sus extremos en los puntos $(0,0)$ y $(a,b)$.

Coordenada x

Coordenada y

Ejercicio 5.17 Calcular de manera aproximada el valor de $\mathrm{sen}(1/2)$ usando los siguientes polinomios de Taylor de la función $f(x)=\mathrm{sen}(x)$.

1. Polinomio de Taylor de grado 20 en el punto $\pi /6$.

   
   

2. Polinomio de MacLaurin de grado 100.

   
   

1. ¿Qué polinomio da una mejor aproximación?

   Select an item

   El polinomio de Taylor de grado 20 en $\pi /6$.

   El polinomio de MacLaurin de grado 100.