2  Sucesiones de números reales

2.1 Ejercicios Resueltos

Para la realización de esta práctica se requieren los siguientes paquetes:

using SymPy  # Para el cálculo simbólico de límites.
using Plots  # Para el dibujo de gráficas.
using Makie # Para obtener gráficos interactivos.
using LaTeXStrings  # Para usar código LaTeX en los gráficos.

Ejercicio 2.1 Dar los 10 primeros términos de las siguientes sucesiones:

  1. \((2n+1)_{n=1}^\infty\)

    Definir una función para el término general y aplicar la función a los naturales de 1 a 10 usando compresiones de arrays.

    a(n) = 2n + 1
println([a(n) for n = 1:10])
    [3, 5, 7, 9, 11, 13, 15, 17, 19, 21]

  2. \(\left(\frac{1}{n}\right)_{n=1}^\infty\)

    # Como reales
a(n) = 1 / n
println([a(n) for n = 1:10])
# Como racionales
a(n) = 1//n
println([a(n) for n = 1:10])
    [1.0, 0.5, 0.3333333333333333, 0.25, 0.2, 0.16666666666666666, 0.14285714285714285, 0.125, 0.1111111111111111, 0.1]
Rational{Int64}[1, 1//2, 1//3, 1//4, 1//5, 1//6, 1//7, 1//8, 1//9, 1//10]

  3. \(\left((-1)^n\right)_{n=1}^\infty\)

    a(n) = (-1)^n
println([a(n) for n = 1:10])
    [-1, 1, -1, 1, -1, 1, -1, 1, -1, 1]

  4. \(\left(\left(1+\frac{1}{n}\right)^n\right)_{n=1}^\infty\)

    a(n) = (1 + 1 / n)^n
println([a(n) for n = 1:10])
    [2.0, 2.25, 2.3703703703703702, 2.44140625, 2.4883199999999994, 2.5216263717421135, 2.546499697040712, 2.565784513950348, 2.5811747917131984, 2.5937424601000023]

  5. \(a_1=1\) y \(a_{n+1}=\sqrt{1+a_n}\) \(\forall n\in\mathbb{N}\)

    a(n) = n == 1 ? 1 : sqrt(1+a(n-1))
println([a(n) for n = 1:10])
    Real[1, 1.4142135623730951, 1.5537739740300374, 1.5980531824786175, 1.6118477541252516, 1.616121206508117, 1.6174427985273905, 1.617851290609675, 1.6179775309347393, 1.6180165422314876]

Ejercicio 2.2 Dibujar en una gráfica los 50 primeros términos de las siguientes sucesiones y deducir si son convergentes o no. En el caso de que sean convergentes, dar un valor aproximado de su límite.

Definir una función para el término general y aplicar la función a los naturales de 1 a 50 usando compresiones de arrays como en el ejercicio anterior. Después usar la función scatter del paquete Plots, o bien la función scatter del paquete Makie, para dibujar el array de términos.

  1. \(\left(\frac{n}{4n+2}\right)_{n=1}^\infty\)

    using Plots
a(n) = n / (4n + 2)
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = n / (4n + 2)
Makie.scatter([a(n) for n = 1:50])

    La sucesión converge al número \(0.25\).

  2. \(\left(\frac{2^n}{n^2}\right)_{n=1}^\infty\)

    using Plots
a(n) = 2^n / (4n + 2)
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = 2^n / (4n + 2)
Makie.scatter([a(n) for n = 1:50])

    La sucesión diverge.

  3. \(\left(\frac{(-1)^n}{n}\right)_{n=1}^\infty\)

    using Plots
a(n) = (-1)^n / n
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = (-1)^n / n
Makie.scatter([a(n) for n = 1:50])

    La sucesión converge al \(0\).

  4. \(\left(\left(1+\frac{1}{n}\right)^n\right)_{n=1}^\infty\)

    using Plots
a(n) = (1 + 1 / n)^n
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = (1 + 1 / n)^n
Makie.scatter([a(n) for n = 1:50])

    La sucesión converge aproximadamente a \(2.7\).

  5. \(a_1 = 0.5\) y \(a_{n+1}=\frac{3}{2+a_n}\) \(\forall n\in\mathbb{N}\)

    using Plots
a(n) =  n == 1 ? 0.5 : 3/(2+a(n-1))
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = n == 1 ? 0.5 : 3/(2+a(n-1))
Makie.scatter([a(n) for n = 1:50])

    La sucesión converge aproximadamente a \(1\).

Ejercicio 2.3 Calcular el límite, si existe, de las siguiente sucesiones.

  1. \(\left(\frac{1}{n}\right)_{n=1}^\infty\)

    Definir una función para el término general y usar la función limit del paquete SymPy para calcular el límite de la sucesión.

    using SymPy
@syms n  # Declaración de la variable simbólica n.
a(n) = 1/n
limit(a(n), n=>oo)

    \(0\)

  2. \(\left((-1)^n\right)_{n=1}^\infty\)

    @syms n
a(n) = (-1)^n
limit(a(n), n=>oo)

    \(\text{NaN}\)

  3. \(\left(\left(1+\frac{1}{n}\right)^n\right)_{n=1}^\infty\)

    @syms n
a(n) = (1 + 1 / n)^n
limit(a(n), n=>oo)

    \(e\)

Ejercicio 2.4 En el siglo III A.C Arquímedes usó el método por agotamiento para calcular el área encerrada por una circunferencia (y de paso el valor de \(\pi\)). La idea consiste en inscribir la circunferencia en polígonos regulares con un número de lados cada vez mayor.

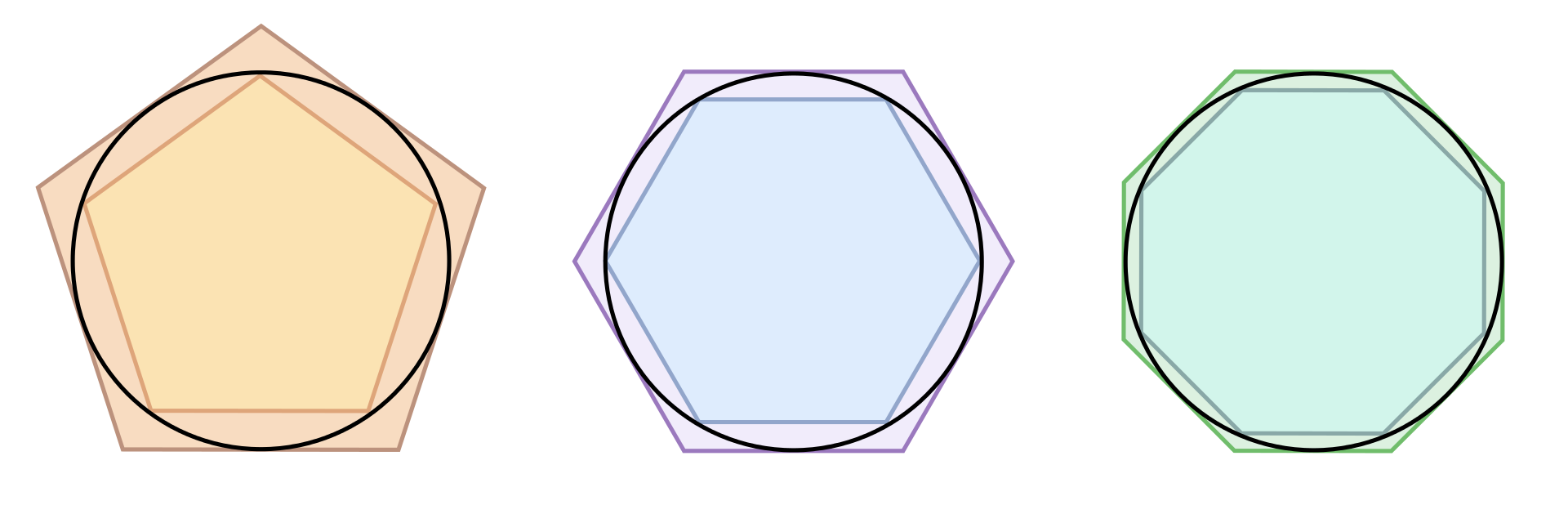
Aproximación del área de una circunferencia mediante polígonos regulares

El área de estos polígonos puede calcularse fácilmente descomponiendo los polígonos regulares en triángulos como en el siguiente ejemplo.

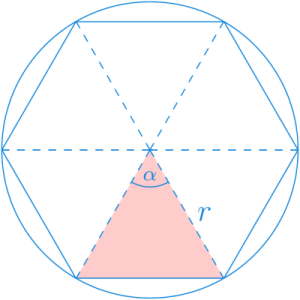
Descomposición de un hexágono en triángulos

En el caso de los polígonos inscritos dentro de la circunferencia, como dos de los lados siempre coinciden con el radio de la circunferencia \(r\), el perímetro del polígon de \(n\) lados puede calcularse con la fórmula

\[ p_n = 2nr\operatorname{sen}\left(\frac{\pi}{n}\right) \]

y el área puede calcularse con la fórmula

\[ a_n = \frac{1}{2}nr^2\operatorname{sen}\left(\frac{2\pi}{n}\right). \]

  1. Calcular el perímetro de los polígonos de \(10^i\) lados, para \(i=1,\ldots, 6\) tomando \(r=1\).

    p(n) = 2n*sin(pi/n)
println([p(10^i) for i = 1:6])
    [6.180339887498948, 6.282151815625658, 6.283174971759127, 6.28318520382533, 6.283185306146043, 6.283185307169251]

  2. Calcular el área de los polígonos de \(10^i\) lados, para \(i=1,\ldots, 6\) tomando \(r=1\).

    a(n) = n*sin(2*pi/n)/2
println([a(10^i) for i = 1:6])
    [2.938926261462366, 3.1395259764656687, 3.1415719827794755, 3.141592446881286, 3.141592651522708, 3.1415926535691225]

  3. Dibujar con los primeros 50 términos de la sucesión de los perímetros de los polígonos tomando \(r=1\).

    using Plots
a(n) = 2n*sin(pi/n)
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = 2n*sin(pi/n)
Makie.scatter([a(n) for n = 1:50])

  4. Dibujar con los primeros 50 términos de la sucesión de las areas de los polígonos tomando \(r=1\).

    using Plots
a(n) = n*sin(2*pi/n)/2
scatter([a(n) for n = 1:50], legend=false)
    using GLMakie
a(n) = n*sin(2*pi/n)/2
Makie.scatter([a(n) for n = 1:50])

  5. Calcular el límite de la sucesión de los perímetros de los polígonos tomando \(r=1\).

    using SymPy
@syms n
a(n) = 2n*sin(PI/n)  # Para cálculo simbólico es mejor utilizar la constante simbólica PI en lugar de pi.
limit(a(n), n=>oo)

    \(2 \pi\)

  6. Usando el resultado anterior, calcular el perímetro del círculo de radio \(r\).

    using SymPy
@syms n, r
a(n) = 2n*r*sin(PI/n)
limit(a(n), n=>oo)

    \(2 \pi r\)

  7. Calcular el límite de la sucesión de las areas de los polígonos tomando \(r=1\).

    using SymPy
@syms n
a(n) = n*sin(2*PI/n)/2
limit(a(n), n=>oo)

    \(\pi\)

  8. Usando el resultado anterior, calcular el area del círculo de radio \(r\).

    using SymPy
@syms n, r
a(n) = n*r^2*sin(2*PI/n)/2
limit(a(n), n=>oo)

    \(\pi r^{2}\)

Ejercicio 2.5 Dada la sucesión \(a_1=1\) y \(a_{n+1}=1+\frac{1}{a_n}\) \(\forall n\in\mathbb{N}\), se pide:

  1. Dibujar la gráfica de los 10 primeros términos de la sucesión. ¿Es una sucesión monótona?

    using Plots
a(n) =  n == 1 ? 1 : 1 + 1 / a(n-1)
scatter([a(n) for n = 1:10], legend=false)
    using GLMakie
a(n) = n == 1 ? 1 : 1 + 1 / a(n-1)
Makie.scatter([a(n) for n = 1:10])

    La sucesión no es monótona.

  2. Dibujar la gráfica de los 5 primeros términos de las subsucesiones con los términos pares e impares. ¿Son monótonas?

    using Plots, LaTeXStrings
a(n) =  n == 1 ? 1 : 1 + 1 / a(n-1)
Plots.scatter([a(2i-1) for i=1:5], label = L"$a_{2n-1}$")
Plots.scatter!([a(2i) for i=1:5], label = L"$a_{2n}$")
    using GLMakie
a(n) = n == 1 ? 1 : 1 + 1 / a(n-1)
fig, ax = Makie.scatter([a(2i-1) for i = 1:5], label = L"$a_{2n-1}$" )
Makie.scatter!(ax,[a(2i) for i=1:5], label = L"$a_{2n}$")
axislegend()
fig

    La sucesión de los términos impares es creciente y la de los pares es decreciente.

2.2 Ejercicios propuestos

Ejercicio 2.6 Calcular el décimo término de la sucesión \(\left(\frac{3n^2+n}{6n^2-1}\right)_{n=1}^\infty\).


 🎁

Ejercicio 2.7 Calcular los 10 primeros términos de la sucesión \(\left(\frac{3n^2+n}{6n^2-1}\right)_{n=1}^\infty\) y averiguar hacia dónde converge.

Select an item

Ejercicio 2.8 ¿Cuál de las siguientes gráficas corresponde a la sucesión \(a_1=3\) y \(a_{n+1}=\sqrt{2a_n}\) \(\forall n\in\mathbb{N}\).

Image for hotspot selection

Ejercicio 2.9 A la vista de la gráfica de los 20 primeros términos de la sucesión \(\left(\frac{2^n}{n!}\right)_{n=1}^\infty\), ¿crees que la sucesión converge?

Select an item

Ejercicio 2.10 A la vista de la gráfica de los 10 primeros términos de la sucesión \(\left(\frac{n^n}{n!}\right)_{n=1}^\infty\), ¿crees que la sucesión converge?

Select an item

Ejercicio 2.11 A la vista de la gráfica de los 20 primeros términos de la sucesión dada por \(a_1=1\) y \(a_{n+1}=\sqrt{a_n+2}\) \(\forall n\in \mathbb{N}\), ¿crees que la sucesión converge?

Select an item

Ejercicio 2.12 ¿Cuál es el límite de la sucesión \(\left(\left(1+\frac{2}{n}\right)^n\right)_{n=1}^\infty\)


 🎁