7 Redes Neuronales

Las redes de neuronas artificiales son un modelo computacional inspirado en el funcionamiento del cerebro humano. Una neurona artificial es una unidad de cómputo bastante simple, que recibe una serie de entradas, las procesa y produce una salida. La salida de una neurona puede ser la entrada de otra neurona, formando así una red de neuronas interconectadas, donde cada conexión tiene un peso asociado. Es esta red, que a veces contiene miles y millones de neuronas, la que dota de gran potencia de cálculo a este modelo, siendo capaces de aprender patrones de datos muy complejos, como imágenes, texto o sonido, y por tanto, se utilizan a menudo en tareas de clasificación o regresión.

El aprendizaje en una red neuronal consiste en ajustar los pesos de las conexiones para minimizar el error entre la salida predicha y la salida real.

7.1 Ejercicios Resueltos

Para la realización de esta práctica se requieren los siguientes paquetes:

library(tidyverse) 
# Incluye los siguientes paquetes:
# - readr: para la lectura de ficheros csv. 
# - dplyr: para el preprocesamiento y manipulación de datos.
# - ggplot2: para la visualización de datos.
library(tidymodels)
# Incluye los siguientes paquetes:
# - recipes: para la preparación de los datos. 
# - parsnip: para la creación de modelos.
# - workflows: para la creación de flujos de trabajo.
# - rsample: para la creación de particiones de los datos.
# - yardstick: para la evaluación de modelos.
# - tune: para la optimización de hiperparámetros.
library(skimr) # para el análisis exploratorio de datos.
library(brulee) # Para entrenar redes neuronales con `torch`.
library(knitr) # para el formateo de tablas.

Ejercicio 7.1 El conjunto de datos cancer-mama.csv contiene información sobre las características de núcleos de células mamarias obtenidas de imágenes digitalizadas tanto de células cancerosas como no cancerosas obtenidas por biopsia. Las variables que contiene son:

ID: Identificador único de la muestra.
Diagnostico: Diagnóstico de la muestra (M: maligno, B: benigno).
Radio: Media de la distancia desde el centro hasta los puntos de la superficie.
Textura: Desviación estándar de la intensidad de gris de los puntos.
Perímetro: Longitud del contorno.
Área: Área de la imagen.
Suavidad: Variación local en la longitud del radio.
Compacidad: Perímetro^2 / Área - 1.0.
Concavidad: Magnitud de las porciones cóncavas del contorno.
Puntos_concavos: Número de puntos cóncavos del contorno.
Simetría: Simetría de la imagen.
Irregularidad: Medida de la irregularidad de la forma.

Crear un dataframe con los datos del archivo cancer-mama.csv.

Solución

library(tidyverse)
# Cargamos los datos del fichero csv en un dataframe.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/cancer-mama.csv", stringsAsFactors = TRUE) |>
    # Convertimos la variable Diagnostico a un factor.
    mutate(Diagnostico = factor(Diagnostico, levels = c("B", "M"), labels = c("Benigno", "Maligno")))
# Mostramos un resumen del dataframe.
glimpse(df)

Rows: 569
Columns: 12
$ ID              <int> 842302, 842517, 84300903, 84348301, 84358402, 843786, …
$ Diagnostico     <fct> Maligno, Maligno, Maligno, Maligno, Maligno, Maligno, …
$ Radio           <dbl> 17.990, 20.570, 19.690, 11.420, 20.290, 12.450, 18.250…
$ Textura         <dbl> 10.38, 17.77, 21.25, 20.38, 14.34, 15.70, 19.98, 20.83…
$ Perimetro       <dbl> 122.80, 132.90, 130.00, 77.58, 135.10, 82.57, 119.60, …
$ Area            <dbl> 1001.0, 1326.0, 1203.0, 386.1, 1297.0, 477.1, 1040.0, …
$ Suavidad        <dbl> 0.11840, 0.08474, 0.10960, 0.14250, 0.10030, 0.12780, …
$ Compacidad      <dbl> 0.27760, 0.07864, 0.15990, 0.28390, 0.13280, 0.17000, …
$ Concavidad      <dbl> 0.30010, 0.08690, 0.19740, 0.24140, 0.19800, 0.15780, …
$ Puntos_Concavos <dbl> 0.14710, 0.07017, 0.12790, 0.10520, 0.10430, 0.08089, …
$ Simetria        <dbl> 0.2419, 0.1812, 0.2069, 0.2597, 0.1809, 0.2087, 0.1794…
$ Irregularidad   <dbl> 0.07871, 0.05667, 0.05999, 0.09744, 0.05883, 0.07613, …

Hacer un análisis exploratorio de los datos.

Solución

library(skimr)
# Realizamos un análisis exploratorio de los datos.
skim(df)

Data summary
Name	df
Number of rows	569
Number of columns	12
_______________________
Column type frequency:
factor	1
numeric	11
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
Diagnostico	0	1	FALSE	2	Ben: 357, Mal: 212

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
ID	1	30371831.43	125020585.61	8670.00	869218.00	906024.00	8813129.00	911320502.00	▇▁▁▁▁
Radio	1	14.13	3.52	6.98	11.70	13.37	15.78	28.11	▂▇▃▁▁
Textura	1	19.29	4.30	9.71	16.17	18.84	21.80	39.28	▃▇▃▁▁
Perimetro	1	91.97	24.30	43.79	75.17	86.24	104.10	188.50	▃▇▃▁▁
Area	1	654.89	351.91	143.50	420.30	551.10	782.70	2501.00	▇▃▂▁▁
Suavidad	1	0.10	0.01	0.05	0.09	0.10	0.11	0.16	▁▇▇▁▁
Compacidad	1	0.10	0.05	0.02	0.06	0.09	0.13	0.35	▇▇▂▁▁
Concavidad	1	0.09	0.08	0.00	0.03	0.06	0.13	0.43	▇▃▂▁▁
Puntos_Concavos	1	0.05	0.04	0.00	0.02	0.03	0.07	0.20	▇▃▂▁▁
Simetria	1	0.18	0.03	0.11	0.16	0.18	0.20	0.30	▁▇▅▁▁
Irregularidad	1	0.06	0.01	0.05	0.06	0.06	0.07	0.10	▆▇▂▁▁

Dibujar un diagrama de relación entre todos los pares de variables del conjunto de datos diferenciando por el diagnóstico.

Ayuda

Se puede utilizar la función ggpairs del paquete GGally para dibujar un diagrama de relación entre todos los pares de variables del conjunto de datos. Asociar el sexo a la dimensión del color.
Solución
library(GGally) ggpairs(df, aes(color = Diagnostico, alpha = 0.5))
Dividir el conjunto de datos en un conjunto de entrenamiento y un conjunto de prueba, con una proporción del 80% para el entrenamiento y el 20% para la prueba, estratificando por el diagnóstico.
Ayuda
Utilizar la función initial_split del paquete rsample para dividir el conjunto de datos en entrenamiento y test.
Parámetros:
- data: el data frame con los datos.
- prop: la proporción del conjunto de datos que se utilizará para el conjunto de entrenamiento (en este caso, 0.8 para el 80%).
- strata: la variable de estratificación (en este caso, Diagnostico) para asegurar que la distribución de clases se mantenga en ambos conjuntos.
Solución
library(tidymodels) # Establecemos la semilla para la reproducibilidad. set.seed(123) # Dividimos el conjunto de datos en un conjunto de entrenamiento y un conjunto de test. df_particion <- initial_split(df, prop = 0.8, strata = "Diagnostico") # Extraemos el conjunto de entrenamiento. df_entrenamiento <- training(df_particion) # Extraemos el conjunto de test. df_test <- testing(df_particion)

Preprocesar el conjunto de entrenamiento para normalizar las variables numéricas.

Solución

# Creamos una receta de preprocesamiento.
receta <- recipe(Diagnostico ~ ., data = df_entrenamiento) |>
    # Normalizamos las variables numéricas.
    step_normalize(all_numeric_predictors())

Construir una red neuronal con una capa oculta de 10 neuronas para predecir el diagnóstico. Realizar solo dos iteraciones (épocas) de entrenamiento.

Ayuda

Utilizar la función mlp del paquete parsnip para crear un modelo de red neuronal.

Parámetros:

hidden_units: el número de neuronas en la capa oculta (10 en este caso).
activation: la función de activación a utilizar (por defecto “relu”).
dropout: la proporción de parámetros reseteados a 0 durante el entrenamiento (0.1 por defecto).
epochs: el número de épocas de entrenamiento (100 por defecto).

Después, utilizar la función set_engine para especificar el motor a utilizar (en este caso, brulee).

Utilizar la función set_mode para especificar que se trata de un modelo de clasificación.

Finalmente, utilizar la función extract_fit_engine para extraer el modelo entrenado del flujo de trabajo.

Solución

library(brulee)
# Establecemos la semilla aleatoria para la reproducibilidad.
set.seed(123)
# Creamos un modelo de red neuronal perceptrón multicapa.
modelo <- mlp(hidden_units = 10, epochs = 2) |>
    # Establecemos el motor de entrenamiento del paquete brulee.
    set_engine("brulee") |>
    # Establecemos el modo de entrenamiento como clasificación.
    set_mode("classification")

# Creamos un flujo de trabajo para entrenar el modelo.
modelo_entrenado <- workflow() |>
    # Añadimos la receta de preprocesamiento.
    add_recipe(receta) |>
    # Añadimos el modelo.
    add_model(modelo) |>
    # Entrenamos el modelo.
    fit(data = df_entrenamiento)

# Mostramos un resumen del modelo.
modelo_entrenado |> extract_fit_engine()

Multilayer perceptron

relu activation,
10 hidden units,
142 model parameters
454 samples, 11 features, 2 classes 
class weights Benigno=1, Maligno=1 
weight decay: 0.001 
dropout proportion: 0 
batch size: 409 
learn rate: 0.01 
validation loss after 2 epochs: 0.152

Evaluar el modelo con el conjunto de test y calcular la matriz de confusión, la exactitud, y el area bajo la curva ROC.
Ayuda
Usar la función augment del paquete parsnip para añadir al conjunto de test las probabilidades cada especie de pingüino.
Parámetros:
- new_data: el conjunto de datos de test.
Usar la función conf_mat del paquete yardstick para calcular la matriz de confusión.
Parámetros:
- truth: la variable respuesta (en este caso, Especie).
- estimate: la variable con las clases predichas por el modelo (en este caso, .pred_class).
Usar la función metrics del paquete yardstick para calcular las métricas de evaluación del modelo.
Parámetros:
- truth: la variable respuesta (en este caso, Especie).
- estimate: la variable con las clases predichas por el modelo (en este case, .pred_class).
Usar la función roc_auc del paquete yardstick para calcular el área bajo la curva ROC.
Parámetros:
- truth: la variable respuesta (en este caso, Especie).
- estimate: la variable con las probabilidades de la clase positiva (en este caso, .pred_Benigno).
Solución
library(knitr) # Añadimos las predicciones al conjunto de test. df_test_2 <- modelo_entrenado |> augment(new_data = df_test) # Calculamos la matriz de confusión. matriz_confusion <- df_test_2 |> conf_mat(truth = Diagnostico, estimate = .pred_class) matriz_confusion$table |> kable()

Benigno Maligno

Benigno 68 3

Maligno 4 40

# Calculamos las métricas de evaluación del modelo con el conjunto de test. df_test_2 |> metrics(truth = Diagnostico, estimate = .pred_class) |> kable()

.metric .estimator .estimate

accuracy binary 0.9391304

kap binary 0.8705996

# Calculamos el área bajo la curva ROC. df_test_2 |> roc_auc(truth = Diagnostico, .pred_Benigno) |> kable()

.metric .estimator .estimate

roc_auc binary 0.993863

	Benigno	Maligno
Benigno	68	3
Maligno	4	40

.metric	.estimator	.estimate
accuracy	binary	0.9391304
kap	binary	0.8705996

.metric	.estimator	.estimate
roc_auc	binary	0.993863

Volver a entrenar la red neuronal anterior con 10 iteraciones (épocas) y evaluar la exactitud del modelo con el conjunto de test.

Ayuda

Utilizar la función mlp del paquete parsnip para crear un modelo de red neuronal.

Parámetros:

hidden_units: el número de neuronas en la capa oculta (10 en este caso).
activation: la función de activación a utilizar (por defecto “relu”).
dropout: la proporción de parámetros reseteados a 0 durante el entrenamiento (0.1 por defecto).
epochs: el número de épocas de entrenamiento (100 por defecto).

Después, utilizar la función set_engine para especificar el motor a utilizar (en este caso, brulee).

Utilizar la función set_mode para especificar que se trata de un modelo de clasificación.

Finalmente, utilizar la función extract_fit_engine para extraer el modelo entrenado del flujo de trabajo.

Solución

# Establecemos la semilla aleatoria para la reproducibilidad.
set.seed(123)
# Creamos un modelo de red neuronal perceptrón multicapa.
modelo <- mlp(hidden_units = 10, epochs = 10) |>
    # Establecemos el motor de entrenamiento del paquete brulee.
    set_engine("brulee") |>
    # Establecemos el modo de entrenamiento como clasificación.
    set_mode("classification")

# Creamos un flujo de trabajo para entrenar el modelo.
modelo_entrenado <- workflow() |>
    # Añadimos la receta de preprocesamiento.
    add_recipe(receta) |>
    # Añadimos el modelo.
    add_model(modelo) |>
    # Entrenamos el modelo.
    fit(data = df_entrenamiento)

# Añadimos las predicciones al conjunto de test.    
df_test_10 <- modelo_entrenado |> augment(new_data = df_test)

# Calculamos las métricas de evaluación del modelo.
df_test_10 |> metrics(truth = Diagnostico, estimate = .pred_class) |>
    kable()

.metric	.estimator	.estimate
accuracy	binary	0.9652174
kap	binary	0.9264000

Ejercicio 7.2 El fichero vinos.csv contiene información sobre las características de vinos blancos y tintos portugueses de la denominación “Vinho Verde”. Las variables que contiene son las siguientes:

Variable	Descripción	Tipo (unidades)
tipo	Tipo de vino	Factor (blanco, tinto)
meses.barrica	Meses de envejecimiento en barrica	Numérica(meses)
acided.fija	Cantidad de ácidotartárico	Numérica(g/dm3)
acided.volatil	Cantidad de ácido acético	Numérica(g/dm3)
acido.citrico	Cantidad de ácidocítrico	Numérica(g/dm3)
azucar.residual	Cantidad de azúcar remanente después de la fermentación	Numérica(g/dm3)
cloruro.sodico	Cantidad de clorurosódico	Numérica(g/dm3)
dioxido.azufre.libre	Cantidad de dióxido de azufre en forma libre	Numérica(mg/dm3)
dioxido.azufre.total	Cantidad de dióxido de azufre total en forma libre o ligada	Numérica(mg/dm3)
densidad	Densidad	Numérica(g/cm3)
ph	pH	Numérica(0-14)
sulfatos	Cantidad de sulfato de potasio	Numérica(g/dm3)
alcohol	Porcentaje de contenido de alcohol	Numérica(0-100)
calidad	Calificación otorgada por un panel de expertos	Numérica(0-10)

Crear un data frame con los datos del archivo vinos.csv.

Solución

library(tidyverse)
# Cargamos los datos del fichero csv en un dataframe.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/vinos.csv", stringsAsFactors = TRUE)
# Mostramos un resumen del dataframe.
glimpse(df)

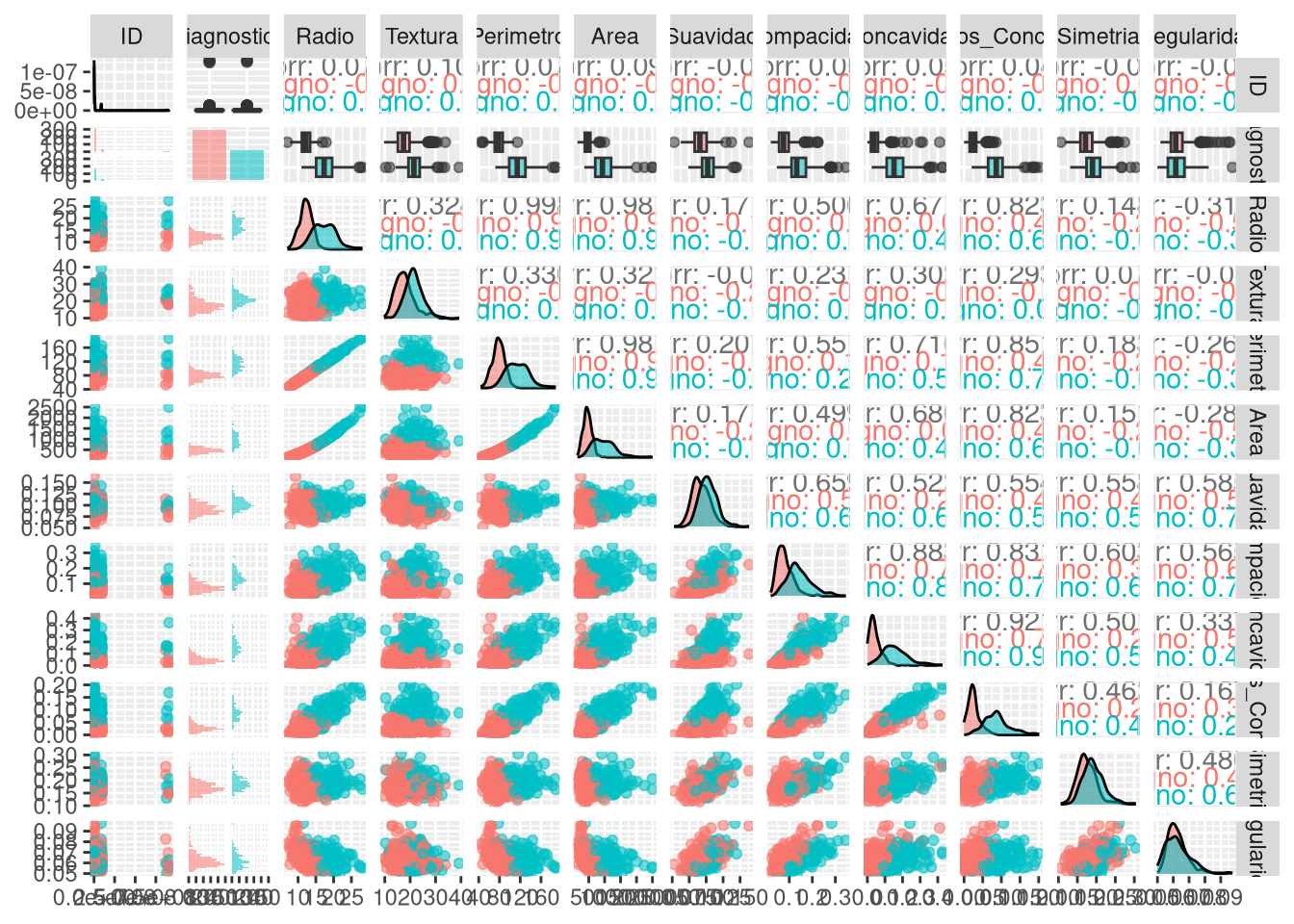
Rows: 5,320
Columns: 14
$ tipo                 <fct> blanco, blanco, blanco, blanco, blanco, blanco, b…
$ meses_barrica        <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ acided_fija          <dbl> 7.0, 6.3, 8.1, 7.2, 6.2, 8.1, 8.1, 8.6, 7.9, 6.6,…
$ acided_volatil       <dbl> 0.27, 0.30, 0.28, 0.23, 0.32, 0.22, 0.27, 0.23, 0…
$ acido_citrico        <dbl> 0.36, 0.34, 0.40, 0.32, 0.16, 0.43, 0.41, 0.40, 0…
$ azucar_residual      <dbl> 20.70, 1.60, 6.90, 8.50, 7.00, 1.50, 1.45, 4.20, …
$ cloruro_sodico       <dbl> 0.045, 0.049, 0.050, 0.058, 0.045, 0.044, 0.033, …
$ dioxido_azufre_libre <dbl> 45, 14, 30, 47, 30, 28, 11, 17, 16, 48, 41, 28, 3…
$ dioxido_azufre_total <dbl> 170, 132, 97, 186, 136, 129, 63, 109, 75, 143, 17…
$ densidad             <dbl> 1.0010, 0.9940, 0.9951, 0.9956, 0.9949, 0.9938, 0…
$ ph                   <dbl> 3.00, 3.30, 3.26, 3.19, 3.18, 3.22, 2.99, 3.14, 3…
$ sulfatos             <dbl> 0.45, 0.49, 0.44, 0.40, 0.47, 0.45, 0.56, 0.53, 0…
$ alcohol              <dbl> 8.8, 9.5, 10.1, 9.9, 9.6, 11.0, 12.0, 9.7, 10.8, …
$ calidad              <int> 6, 6, 6, 6, 6, 6, 5, 5, 5, 7, 5, 7, 6, 8, 6, 5, 7…

Realizar un análisis exploratorio de los datos.

Solución

library(skimr)
# Realizamos un análisis exploratorio de los datos.
skim(df)

Data summary
Name	df
Number of rows	5320
Number of columns	14
_______________________
Column type frequency:
factor	1
numeric	13
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
tipo	0	1	FALSE	2	bla: 3961, tin: 1359

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
meses_barrica	1	1.23	3.14	0.00	0.00	0.00	0.00	24.00	▇▁▁▁▁
acided_fija	1	7.22	1.32	3.80	6.40	7.00	7.70	15.90	▂▇▁▁▁
acided_volatil	1	0.34	0.17	0.08	0.23	0.30	0.41	1.58	▇▂▁▁▁
acido_citrico	1	0.32	0.15	0.00	0.24	0.31	0.40	1.66	▇▅▁▁▁
azucar_residual	1	5.03	4.41	0.60	1.80	2.70	7.50	26.05	▇▂▁▁▁
cloruro_sodico	1	0.06	0.04	0.01	0.04	0.05	0.07	0.61	▇▁▁▁▁
dioxido_azufre_libre	1	30.04	17.81	1.00	16.00	28.00	41.00	289.00	▇▁▁▁▁
dioxido_azufre_total	1	114.11	56.77	6.00	74.00	116.00	153.25	440.00	▅▇▂▁▁
densidad	1	0.99	0.00	0.99	0.99	0.99	1.00	1.04	▇▂▁▁▁
ph	1	3.22	0.16	2.72	3.11	3.21	3.33	4.01	▁▇▆▁▁
sulfatos	1	0.53	0.15	0.22	0.43	0.51	0.60	2.00	▇▃▁▁▁
alcohol	1	10.55	1.19	8.00	9.50	10.40	11.40	14.90	▃▇▅▂▁
calidad	1	5.80	0.88	3.00	5.00	6.00	6.00	9.00	▁▆▇▃▁

Recodificar la variable calidad en una variable categórica con las siguientes categorías:

Muy malo: 1-2
Malo: 3-4
Regular: 5
Bueno: 6
Muy bueno: 7-8
Excelente: 9-10

Solución

df <- df |>
    # Convertimos la variable calidad a un factor recodificando sus valores en distintas categorías.
    mutate(calidad = factor(case_when(
        calidad %in% c(1, 2) ~ "Muy malo",
        calidad %in% c(3, 4) ~ "Malo",
        calidad == 5 ~ "Regular",
        calidad == 6 ~ "Bueno",
        calidad %in% c(7, 8) ~ "Muy bueno",
        TRUE ~ "Excelente"
    ), levels = c("Muy malo", "Malo", "Regular", "Bueno", "Muy bueno", "Excelente")))

Mostrar la tabla de frecuencias de la variable calidad.
Solución
library(knitr) # Obtenemos la tabla de frecuencias de la variable calidad. df |> count(calidad) |> kable()

calidad n

Malo 236

Regular 1752

Bueno 2323

Muy bueno 1004

Excelente 5

calidad	n
Malo	236
Regular	1752
Bueno	2323
Muy bueno	1004
Excelente	5

Dividir el conjunto de datos en un conjunto de entrenamiento (80%) y un conjunto de prueba (20%) estratificando por la variable calidad.

Solución

library(tidymodels)
# Establecemos la semilla aleatoria para la reproducibilidad.
set.seed(123)
# Dividimos el conjunto de datos en un conjunto de entrenamiento (80%) y un conjunto de test (20%) estratificando por la variable calidad.
df_particion <- initial_split(df, prop = 0.8, strata = "calidad")
# Extraemos el conjunto de datos de entrenamiento.
df_entrenamiento <- training(df_particion)
# Extraemos el conjunto de datos de test.
df_test <- testing(df_particion)

Establecer la calidad como variable objetivo, normalizar las variables predictivas y convertir las variables categóricas en variables numéricas dummy.

Solución

# Definimos la receta de preprocesamiento indicando que la variable respuesta es calidad y el resto son variables predictivas.
receta <- recipe(calidad ~ ., data = df_entrenamiento) |> 
    # Normalizamos las variables numéricas.
    step_normalize(all_numeric_predictors()) |> 
    # Convertimos las variables categóricas en variables dummy.
    step_dummy(all_nominal_predictors())

Construir una red neuronal para predecir la calidad del vino explorando distintos valores para el número de neuronas en la capa oculta (10, 15, 20, 25) mediante validación cruzada con 5 pliegues. Utilizar la precisión y el área bajo la curva ROC como métricas de evaluación.

Ayuda

Utilizar la función tune() del paquete hardhat para definir los parámetros a optimizar. En este caso, se pueden definir los siguientes parámetros:

hidden_units: el número de neuronas en la capa oculta.

Después, utilizar la función tune_grid del paquete tune para optimizar los parámetros del modelo de la red neuronal.

Parámetros:

resamples: el conjunto de datos de entrenamiento particionado en pliegues para validación cruzada (en este caso, vfold_cv(df_entrenamiento, v = 5)).
grid: un data frame con los valores de los parámetros a probar.

Usar la función autoplot() del paquete tune para visualizar los resultados de la optimización.

Solución

library(brulee)
# Semilla aleatoria para la reproducibilidad.****
set.seed(123) 
# Creamos un modelo de red neuronal perceptrón multicapa con un número variable de neuronas en la capa oculta.
modelo <- mlp(hidden_units = tune()) |>
    # Establecemos el motor de entrenamiento del paquete brulee.
    set_engine("brulee") |>
    # Establecemos el modo de entrenamiento como clasificación.
    set_mode("classification")

# Creamos un flujo de trabajo para entrenar el modelo.
flujo <- workflow() |>
    # Añadimos la receta de preprocesamiento.
    add_recipe(receta) |>
    # Añadimos el modelo.
    add_model(modelo)

# Entrenamos los modelos con diferentes valores de neuronas en la capa oculta.
modelos_entrenados <- flujo |>
    tune_grid(
        resamples = vfold_cv(df_entrenamiento, v = 5), # Validación cruzada con 5 pliegues.
        control = control_grid(save_pred = TRUE), # Guardamos las predicciones.
        grid = tibble(hidden_units = seq(10, 25, by = 5)), # Valores de neuronas a probar.
        metrics = metric_set(accuracy, roc_auc) # Métricas de evaluación.
    ) 

# Visualizamos los resultados de la validación cruzada.
autoplot(modelos_entrenados)

Seleccionar el mejor modelo según la exactitud y entrenarlo con el conjunto de entrenamiento.

Solución

modelo_final <- flujo |>
    # Seleccionamos el mejor modelo según la exactitud.
    finalize_workflow(select_best(modelos_entrenados, metric = "accuracy")) |> 
    # Entrenamos el modelo con el conjunto de entrenamiento.
    last_fit(df_particion, metrics = metric_set(accuracy, roc_auc))

# Mostramos un resumen del modelo.
modelo_final |> extract_fit_engine()

Multilayer perceptron

relu activation,
25 hidden units,
506 model parameters
4,255 samples, 13 features, 6 classes 
class weights Muy malo=1, Malo=1, Regular=1, Bueno=1, Muy bueno=1, Excelente=1 
weight decay: 0.001 
dropout proportion: 0 
batch size: 3830 
learn rate: 0.01 
validation loss after 13 epochs: 0.874

Evaluar el modelo con el conjunto de test y la exactitud y el área bajo la curva ROC.
Solución
# Extraemos las métricas de evaluación del modelo entrenado. collect_metrics(modelo_final) |> kable()

.metric .estimator .estimate .config

accuracy multiclass 0.6018779 Preprocessor1_Model1

roc_auc hand_till 0.8050608 Preprocessor1_Model1

.metric	.estimator	.estimate	.config
accuracy	multiclass	0.6018779	Preprocessor1_Model1
roc_auc	hand_till	0.8050608	Preprocessor1_Model1

7.2 Ejercicios Propuestos

Ejercicio 7.3 El fichero infartos.csv contiene información sobre distintas variables fisiológicas relacionadas con el riesgo de infarto de una muestra de personas. Las variables que contienen son:

Edad: Edad del paciente (años)
Sexo: Sexo del paciente (H: hombre, M: mujer)
DolorPecho: Tipo de dolor torácico (TA: angina típica, ATA: angina atípica, NAP: dolor no anginoso, ASY: asintomático)
PresionArterial: Presión arterial sistólica en reposo (mm Hg)
Colesterol: Colesterol sérico (mm/dl)
Glucemia: Glucemia en ayunas (1: si glucemia en ayunas > 120 mg/dl, 0: de lo contrario)
Electro: resultados del electrocardiograma en reposo (Normal: normal, ST: anomalía onda ST-T (inversiones de onda T y/o elevación o depresión de ST > 0,05 mV), LVH: hipertrofia ventricular izquierda probable o definitiva según criterios de Estes)
Pulsaciones: Frecuencia cardíaca máxima alcanzada (valor numérico entre 60 y 202)
AnginaEjercicio: Angina inducida por ejercicio (S: sí, N: no)
DepresionST: Depresión del segmento ST inducida por el ejercicio (valor numérico de la depresión).
PendienteST: Pendiente del segmento ST en el pico de ejercicio (Ascendente, Plano, Descencdente).
Infarto: Riesgo de infarto (1: Sí, 0: No)

Crear un dataframe con los datos del archivo infartos.csv.
Realizar un análisis exploratorio de los datos.
Dividir el conjunto de datos en dos subconjuntos, uno de entrenamiento y otro de test. Utilizar el 80% de los datos para entrenamiento y el 20% restante para test.
Construir una red neuronal para predecir el riesgo de infarto explorando distinto número de neuronas en la capa oculta y validando los modelos mediante validación cruzada de 5 pliegues. ¿Qué número de neuronas tiene el mejor modelo según la exactitud?
Entrenar el mejor modelo del apartado anterior con el conjunto de entrenamiento y evaluarlo con el conjunto de test. Calcular la matriz de confusión y también la precisión, sensibilidad y la especificidad.