3  Aprendizaje no supervisado

El aprendizaje no supervisado abarca técnicas de aprendizaje automático que buscan identificar patrones en los datos sin utilizar clases o categorías predefinidas. A diferencia del aprendizaje supervisado, donde se entrena un modelo con datos etiquetados, el aprendizaje no supervisado no busca clasificar o predecir una variable respuesta, sino que se centra en descubrir estructuras ocultas en los datos. En esta práctica, exploraremos dos técnicas comunes de aprendizaje no supervisado: el análisis de componentes principales (PCA) que consiste en buscar una representación de los datos en un espacio de menor dimensión preservando la mayor cantidad de varianza posible, y el agrupamiento (clustering) que busca agrupar los datos en grupos similares basándose en sus características. Estas técnicas son útiles para la exploración de datos, la reducción de dimensionalidad y la identificación de patrones subyacentes en conjuntos de datos complejos.

3.1 Ejercicios Resueltos

Para la realización de esta práctica se requieren los siguientes paquetes:

library(tidyverse) 
# Incluye los siguientes paquetes:
# - readr: para la lectura de ficheros csv. 
# - dplyr: para el preprocesamiento y manipulación de datos.
# - ggplot2: para la visualización de datos.
library(tidymodels)
# Incluye los siguientes paquetes:
# - recipes: para la preparación de los datos. 
# - parsnip: para la creación de modelos.
# - workflows: para la creación de flujos de trabajo.
# - rsample: para la creación de particiones de los datos.
# - yardstick: para la evaluación de modelos.
# - tune: para la optimización de hiperparámetros.
library(skimr) # para el análisis exploratorio de datos.
library(GGally) # para la visualización de matrices de correlación.
library(FactoMineR) # para el análisis de componentes principales.
library(factoextra) # para dibujar los componentes principales.
library(psych) # para el cálculo de la kappa de Cohen.
library(plotly) # para la visualización interactiva de gráficos.
library(knitr) # para el formateo de tablas.

Ejercicio 3.1 El conjunto de datos pingüinos.csv contiene un conjunto de datos sobre tres especies de pingüinos con las siguientes variables:

  • Especie: Especie de pingüino (Adelie, Chinstrap o Gentoo).
  • Isla: Isla del archipiélago Palmer donde se realizó la observación.
  • Longitud_pico: Longitud del pico (mm).
  • Profundidad_pico: Profundidad del pico (mm)
  • Longitud_ala: Longitud de la aleta en (mm).
  • Peso: Masa corporal (g).
  • Sexo: Sexo (macho, hembra)

  1. Cargar los datos del archivo pingüinos.csv en un data frame.

    library(tidyverse)
# Cargamos el conjunto de datos en un data frame.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/pingüinos.csv", stringsAsFactors = TRUE)
# Mostramos un resumen del data frame.
glimpse(df)
    Rows: 344
Columns: 7
$ Especie          <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adeli…
$ Isla             <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgersen…
$ Longitud_pico    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, 4…
$ Profundidad_pico <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, 2…
$ Longitud_ala     <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186,…
$ Peso             <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, 4…
$ Sexo             <fct> macho, hembra, hembra, NA, hembra, macho, hembra, mac…

  2. Realizar un análisis exploratorio de los datos.

    library(skimr)
# Análisis exploratorio de los datos.
skim(df)
    Data summary
    Name df
    Number of rows 344
    Number of columns 7
    _______________________
    Column type frequency:
    factor 3
    numeric 4
    ________________________
    Group variables None

    Variable type: factor

    skim_variable n_missing complete_rate ordered n_unique top_counts
    Especie 0 1.00 FALSE 3 Ade: 152, Gen: 124, Chi: 68
    Isla 0 1.00 FALSE 3 Bis: 168, Dre: 124, Tor: 52
    Sexo 11 0.97 FALSE 2 mac: 168, hem: 165

    Variable type: numeric

    skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
    Longitud_pico 2 0.99 43.92 5.46 32.1 39.23 44.45 48.5 59.6 ▃▇▇▆▁
    Profundidad_pico 2 0.99 17.15 1.97 13.1 15.60 17.30 18.7 21.5 ▅▅▇▇▂
    Longitud_ala 2 0.99 200.92 14.06 172.0 190.00 197.00 213.0 231.0 ▂▇▃▅▂
    Peso 2 0.99 4201.75 801.95 2700.0 3550.00 4050.00 4750.0 6300.0 ▃▇▆▃▂

  3. Eliminar del data frame las columnas Isla, Sexo y Peso y eliminar las filas con valores perdidos.

    # Eliminamos las columnas Isla, Sexo y Peso.
df <- df |> select(-Isla, -Sexo, -Peso) |>
    # Eliminamos las filas con valores perdidos.
    drop_na()

  4. Realizar un análisis de correlación entre las variables numéricas del conjunto de datos.

    Utilizar la función ggcorr del paquete GGally para dibujar un diagrama de correlación entre las variables numéricas del conjunto de datos.

    Parámetros:
    • label = TRUE para mostrar las etiquetas de correlación.
    library(GGally)
ggcorr(df, label = TRUE)

  5. Realizar un diagrama de dispersión tridimensional de las variables Longitud_pico, Profundidad_pico y Longitud_ala coloreando los puntos según la especie de pingüino.

    Utilizar la función plot_ly del paquete plotly para dibujar un diagrama de dispersión tridimensional.

    Parámetros:
    • x = Longitud_pico, y = Profundidad_pico, z = Longitud_ala para indicar las variables a utilizar.
    • color = Especie para colorear los puntos según la especie de pingüino.
    library(plotly)
# Diagrama de dispersión tridimensional de las variables Longitud_pico, Profundidad_pico y Longitud_ala. Coloreamos los puntos según la especie de pingüino.
df |> plot_ly(x = ~Longitud_pico, y = ~Profundidad_pico, z = ~Longitud_ala, 
        color = ~Especie,
        type = "scatter3d", mode = "markers") |>
    layout(title = "Diagrama de dispersión tridimensional de pingüinos",
        scene = list(xaxis = list(title = "Longitud del Pico (mm)"),
                        yaxis = list(title = "Profundidad del Pico (mm)"),
                        zaxis = list(title = "Longitud de la Aleta (mm)")))

  6. Calcular los componentes principales del conjunto de variables numéricas y mostrar la varianza explicada por cada componente.

    Utilizar la función PCA del paquete FactoMineR para obtener los componentes principales del conjunto de variables numéricas.

    Parámetros:
    • scale.unit = TRUE para normalizar las variables.
    • ncp = n para obtener los primeros n componentes principales.

    O bien utilizar la función recipe del paquete recipes incluido en la colección de paquetes tidymodels para crear una receta de preprocesamiento.

    Parmámetros:
    • ~. para indicar que se deben utilizar todas las variables.

    Después, utilizar la función step_pca para calcular los componentes principales.

    Parámetros:
    • all_numeric_predictors() para indicar que se deben utilizar todas las variables numéricas.
    • threshold = 0.95 para indicar el umbral de varianza explicada por los componentes principales. Esto significa que se seleccionarán los componentes principales que expliquen al menos el 95% de la varianza total.
    • num_comp = n para indicar el número de componentes principales a calcular.

    Previamente es recomendable normalizar las variables numéricas con la función step_normalize.

    library(FactoMineR)
library(knitr)
# Seleccionamos las variables numéricas.
componentes <- df |> select(where(is.numeric)) |>
    # Calculamos los componentes principales.
    PCA(scale.unit = TRUE, graph = FALSE)   

# Mostramos los autovalores y varianza explicada.
kable(componentes$eig)
    eigenvalue percentage of variance cumulative percentage of variance
    comp 1 2.0031197 66.77066 66.77066
    comp 2 0.7668040 25.56013 92.33079
    comp 3 0.2300763 7.66921 100.00000 
    # Dibujamos un gráfico de la varianza explicada
library(factoextra)
fviz_eig(componentes, addlabels = TRUE)

    library(tidymodels)
# Creamos una receta de preprocesamiento.
receta <- df |> recipe(~ .) |>
    # Normalizamos las variables numéricas.
    step_normalize(all_numeric_predictors()) |>
    # Calculamos los componentes principales con un umbral de varianza del 95%.
    step_pca(all_numeric_predictors(), threshold = 0.95, id = "pca") |>
    # Estimamos los parámetros necesarios para aplicar la receta.
    prep()

# Obtenemos la varianza explicada con cada componente principal.
receta |> tidy(id = "pca", type = "variance") |> 
    # Filtramos los términos para quedarnos con el porcentaje de varianza.
    filter(terms == "percent variance") |> 
    # Dibujamos un diagrama de barras de la varianza explicada.
    ggplot(aes(x = `component`, y = value)) +
    geom_col() +
    labs(title = "Varianza explicada por los componentes principales",
        x = "Componentes Principales",
        y = "Porcentaje de Varianza") 

    # Aplicamos la receta a los datos.
df_componentes <- receta |> bake(new_data = NULL)

  7. Mostrar los autovectores

    Utilizar la función get_pca_var del paquete factoextra para obtener los autovectores de los componentes principales.

    Parámetros:
    • componentes para indicar el objeto con los componentes principales.
    # Obtenemos los autovectores. 
autovectores <- get_pca_var(componentes)
kable(autovectores$coord)
    Dim.1 Dim.2 Dim.3
    Longitud_pico 0.7797577 0.5753925 -0.2467821
    Profundidad_pico -0.7253003 0.6593350 0.1980323
    Longitud_ala 0.9322216 0.0316976 0.3604970 
    # Gráfico de los autovectores
fviz_pca_var(componentes, col.var = "contrib")

  8. Dibujar un gráfico de dispersión de los dos primeros componentes principales coloreando los puntos según la especie de pingüino.

    Utilizar la función fviz_pca_ind del paquete factoextra para dibujar un gráfico de dispersión de los dos primeros componentes principales.

    Parámetros:
    • componentes para indicar el objeto con los componentes principales.
    • col.ind = df$Especie para colorear los puntos según la especie de pingüino.
    # Diagrama de dispersión de los dos primeros componentes principales.
grafico <- componentes |> fviz_pca_ind(col.ind = df$Especie, label = "none") +
    labs(title = "Diagrama de dispersión de los dos primeros componentes principales según Especie",
        x = "Componente Principal 1",
        y = "Componente Principal 2")
# Convertimos el gráfico en interactivo.
ggplotly(grafico) 
    # Diagrama de dispersión de los dos primeros componentes principales.
grafico <- df_componentes  |>  ggplot(aes(x = PC1, y = PC2, color = Especie)) +
    geom_point() +
    labs(title = "Diagrama de dispersión de los dos primeros componentes principales según Especie",
        x = "Componente Principal 1",
        y = "Componente Principal 2")
# Convertimos el gráfico a interactivo
ggplotly(grafico)

  9. Realizar un agrupamiento en grupos utilizando el método de las \(k\)-medias y representar los grupos en un diagrama de dispersión.

    Utilizar la función fviz_nbclust del paquete factoextra para determinar el número óptimo de grupos.

    Parámetros:
    • kmeans para utilizar el método de las \(k\)-medias.
    • method = "wss" para utilizar el método del codo (within-cluster sum of squares).

    Después, utilizar la función kmeans del paquete stats para realizar el agrupamiento en grupos.

    Parámetros:
    • centers = n para indicar el número de grupos a crear.

    O bien utilizar la funicón k_means del paquete tidyclust para especificar un modelo detidymodels para realizar el agrupamiento en grupos.

    Parámetros:
    • num_clusters = n para indicar el número de grupos a crear.

    Usar después la función augment del paquete parsnip para obtener el grupo asignado a cada pingüino.

    # Establecemos una semilla para la reproducibilidad.
set.seed(123)

# Seleccionamos las variables numéricas.
df |> select(where(is.numeric)) |>
    # Determinamos el número óptimo de grupos.
    fviz_nbclust(kmeans, method = "wss")

    A la vista del gráfico anterior, el número óptimo de grupos, donde se ubica el “codo” del gráfico, sería 3 o 4, lo que se corresponde con las 3 especies de pingüinos.

    # Seleccionamos las variables numéricas.
agrupacion <- df |> select(where(is.numeric)) |> 
    # Realizamos el agrupamiento en 3 grupos.
    kmeans(centers = 3)

# Añadimos los grupos al data frame original.
df$Grupo <- as.factor(agrupacion$cluster)

# Dibujamos un diagrama de dispersión de los dos primeros componentes principales coloreando los puntos según el grupo.
componentes |> fviz_pca_ind(col.ind = df$Grupo, label = "none") +
    labs(title = "Diagrama de dispersión de los dos primeros componentes principales según Grupo",
        x = "Componente Principal 1",
        y = "Componente Principal 2")

    library(tidyclust)
# Establecemos una semilla para la reproducibilidad.
set.seed(123)
# Creamos un modelo de agrupamiento en 3 grupos.
modelo_ajustado <- k_means(num_clusters = 3) |>
    # Especificamos el motor a utilizar.
    set_engine("stats") |> 
    # Ajustamos el modelo a los datos.
    fit(~., data = df)

# Creamos un nuevo data frame con los datos del conjunto de datos original y los grupos asignados.
df_grupos <- modelo_ajustado |> augment(df)
# Mostramos el data frame con los grupos asignados.
df_grupos |> head() |> 
    kable()
    Especie Longitud_pico Profundidad_pico Longitud_ala Grupo .pred_cluster
    Adelie 39.1 18.7 181 3 Cluster_1
    Adelie 39.5 17.4 186 3 Cluster_1
    Adelie 40.3 18.0 195 1 Cluster_2
    Adelie 36.7 19.3 193 3 Cluster_1
    Adelie 39.3 20.6 190 3 Cluster_1
    Adelie 38.9 17.8 181 3 Cluster_1 
    # Creamos un data frame con lo valores de los componentes principales y el grupo asignado.
df_componentes <- df_componentes |> 
    mutate(Grupo = df_grupos$.pred_cluster)

# Dibujamos un diagrama de dispersión de los dos primeros componentes principales coloreando los puntos según el grupo.
df_componentes |> 
    ggplot(aes(x = PC1, y = PC2, color = Grupo)) +
    geom_point() +
    labs(title = "Diagrama de dispersión de los dos primeros componentes principales según Grupo",
        x = "Componente Principal 1",
        y = "Componente Principal 2")

  10. Obtener una tabla de contingencia para ver la relación entre las especies de pingüinos y los grupos obtenidos.

    # Creamos una tabla de contingencia con la Especie en las filas y el Grupo en las columnas.
table(df$Especie, df$Grupo) |> 
    kable()
    1 2 3
    Adelie 38 2 111
    Chinstrap 54 5 9
    Gentoo 1 122 0

  11. Calcular la kappa de Cohen para ver la concordancia entre las especies de pingüinos y los grupos obtenidos.

    Utilizar la función cohen.kappa del paquete irr para calcular la kappa de Cohen.

    Parámetros:
    • cbind(df$Especie, df$Grupo) dataframe con las dos variables a comparar.
    library(psych)
# Calculamos la kappa de Cohen.
cohen.kappa(cbind(df$Especie, df$Grupo)) |> 
    tidy() |>
    kable()
    type estimate conf.low conf.high
    unweighted -0.2880626 -0.3391944 -0.2369307
    weighted -0.2921709 -0.3689566 -0.2153852

  12. Realizar un análisis de agrupamiento jerárquico de las especies de pingüinos y dibujar el dendograma asociado coloreando los puntos según la especie de pingüino.

    Utilizar la función hclust del paquete stats para realizar el análisis de agrupamiento jerárquico.

    Parámetros:
    • dist para calcular la matriz de distancias entre las observaciones.
    • method = "complete" para utilizar el método de enlace completo.

    Utilizar la función fviz_dend del paquete factoextra para dibujar el dendograma.

    Parámetros:
    • k = n para crear n grupos.
    • color_labels_by_k = TRUE para colorear las etiquetas según el grupo.
    • rect = TRUE para dibujar rectángulos alrededor de los grupos.
    • rect_fill = TRUE para rellenar los rectángulos.
    # Calculamos la matriz de distancias.
distancias <- df |> select(where(is.numeric)) |> 
    dist(method = "euclidean")
# Realizamos el agrupamiento jerárquico.    
jerarquia <- hclust(distancias, method = "complete")
# Dibujamos un dendrograma coloreado por especie.
fviz_dend(jerarquia, 
    k = 3,  # número de grupos
    color_labels_by_k = TRUE,
    rect = TRUE,
    rect_fill = TRUE) +
labs(title = "Dendrograma de agrupamiento Jerárquico de Pingüinos")

Ejercicio 3.2 El conjunto de datos glaucoma.csv contiene información sobre el grosor de los sectores de los anillos peripalilares de la capa de fibras nerviosas de la retina obtenidos mediante tomografía de coherencia óptica (OTC) en pacientes con y sin glaucoma. En la OTC se toman 4 anillos con distintos radios (BMO, 3.5 mm, 4.1 mm y 4.7 mm) y para cada anillo se miden 6 sectores (Nasal Superior, Nasal, Nasal Inferior, Temporal Inferior, Temporal y Temporal Superior) y también la media global. Los datos están ya normalizados.

Tomografía de coherencia óptica

  1. Cargar el conjunto de datos del archivo glaucoma.csv en un data frame.

    library(tidyverse)
# Cargamos el conjunto de datos en un data frame.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/glaucoma.csv", stringsAsFactors = TRUE)
# Mostramos un resumen del data frame.
glimpse(df)
    Rows: 991
Columns: 31
$ Id           <fct> 28-2017-11-28-L, 90-2017-11-24-L, 106-2017-10-25-L, 170-2…
$ Ojo          <fct> I, I, I, I, I, I, I, I, I, I, I, I, I, I, I, I, I, I, I, …
$ Glaucoma     <fct> No, No, No, No, No, No, No, No, No, No, No, No, No, No, N…
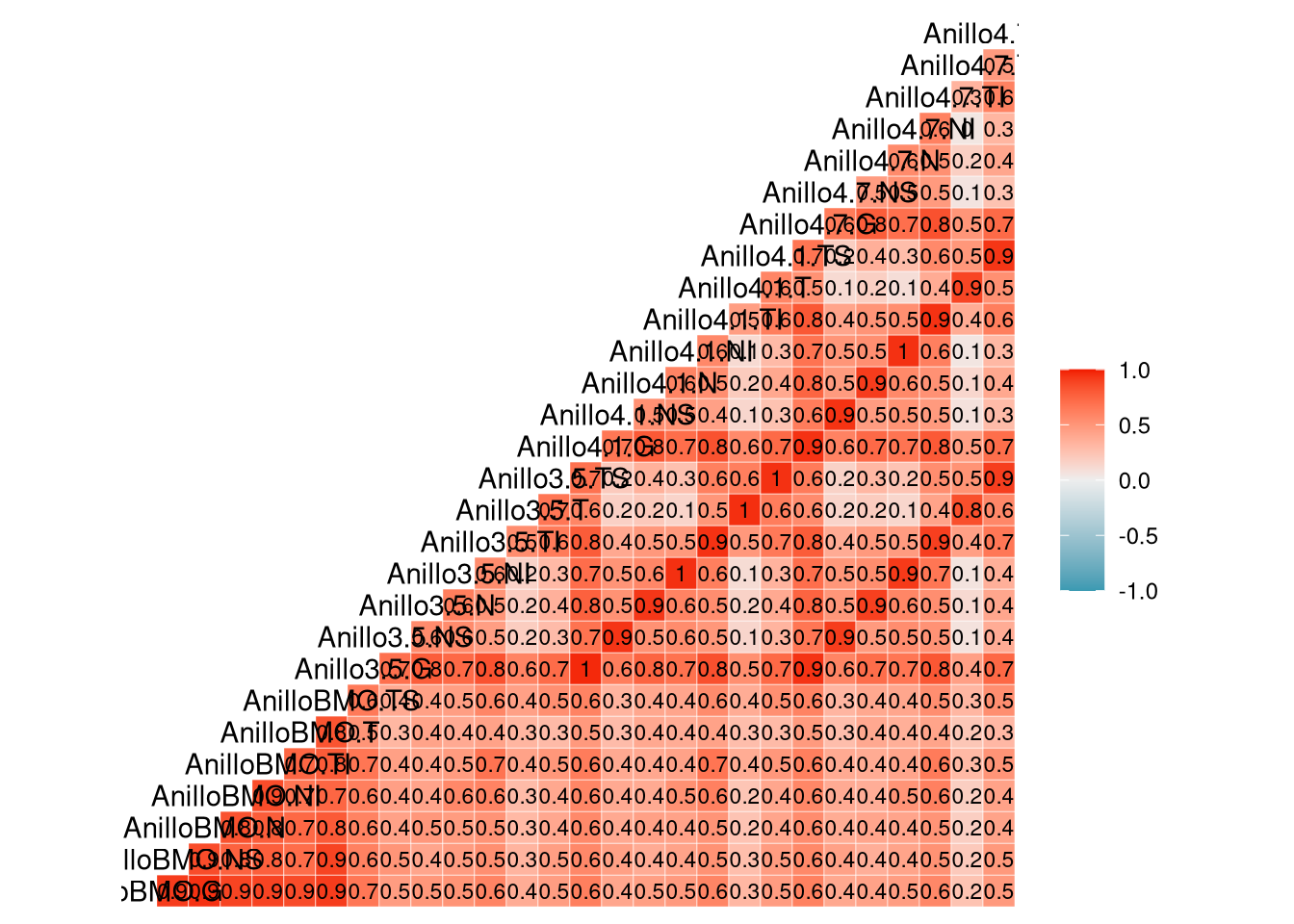
$ AnilloBMO.G  <dbl> -0.80439347, 0.19282278, -0.14995594, -0.24608299, 0.6777…
$ AnilloBMO.NS <dbl> -0.79143813, 0.36651404, 0.39448008, 0.57304030, 1.618783…
$ AnilloBMO.N  <dbl> -0.52772777, -0.02541891, -0.71402835, -0.62100162, 1.025…
$ AnilloBMO.NI <dbl> -0.35277668, 0.19875609, -0.15638019, -0.89208610, -0.473…
$ AnilloBMO.TI <dbl> -0.7528896, 0.4451767, 0.6652916, -0.6153245, -0.2522384,…
$ AnilloBMO.T  <dbl> -0.7439764, -0.1896643, -0.1330641, 0.3428515, 0.2142339,…
$ AnilloBMO.TS <dbl> -1.39159694, 0.75238535, 0.16532422, 0.34138752, 0.816866…
$ Anillo3.5.G  <dbl> -0.09556442, 1.00585070, 0.70929372, 0.76493558, -1.40076…
$ Anillo3.5.NS <dbl> 0.33379621, 0.09117589, 0.06266397, 0.72091790, 0.4400156…
$ Anillo3.5.N  <dbl> 1.28748152, 0.98044192, 0.13244712, 0.30738152, -1.045105…
$ Anillo3.5.NI <dbl> 1.15894330, -0.31496251, 0.39015716, 0.31730079, -0.94341…
$ Anillo3.5.TI <dbl> -0.50311018, 1.31127118, 1.27014639, 1.76714083, -1.79928…
$ Anillo3.5.T  <dbl> -1.59142163, 0.12744265, 0.24522082, -0.79909388, -0.5739…
$ Anillo3.5.TS <dbl> -2.0908403, 1.2527074, 0.5944370, 0.8777833, -0.6874193, …
$ Anillo4.1.G  <dbl> -0.121436081, 1.254674054, 0.430187973, 0.417280946, -1.2…
$ Anillo4.1.NS <dbl> 0.8613243, 0.4950556, 0.1578275, 0.5188949, 0.2699992, 0.…
$ Anillo4.1.N  <dbl> 1.001114455, 1.260064455, 0.157680792, -0.156110297, -1.0…
$ Anillo4.1.NI <dbl> 1.3984707, -0.4752512, 0.1857529, 0.2147013, -0.9788313, …
$ Anillo4.1.TI <dbl> -0.2534641, 1.3862449, 1.1514398, 1.6031777, -2.3624990, …
$ Anillo4.1.T  <dbl> -1.65337057, 0.37802261, 0.19480648, -1.09897557, -0.6063…
$ Anillo4.1.TS <dbl> -2.32056169, 1.18380488, 0.09630482, 1.17049000, 0.121032…
$ Anillo4.7.G  <dbl> 0.08050894, 0.71157788, 0.30403470, 0.47251652, -1.301118…
$ Anillo4.7.NS <dbl> 0.82503033, 0.49344645, 0.52241046, 0.48707283, 0.0209695…
$ Anillo4.7.N  <dbl> 1.15564635, 1.07853988, 0.05617859, -0.03282918, -1.07153…
$ Anillo4.7.NI <dbl> 1.25933229, -0.44207257, 0.05404354, 0.10509507, -0.59378…
$ Anillo4.7.TI <dbl> -0.07477907, 0.19373664, 1.02114279, 1.52007321, -2.53674…
$ Anillo4.7.T  <dbl> -1.43681500, 0.29942282, 0.20263910, -1.08148756, -0.6537…
$ Anillo4.7.TS <dbl> -1.683414795, 0.668934521, -0.478766027, 0.886482740, 0.2…

  2. Realizar un análisis exploratorio de los datos.

    library(skimr)
# Análisis exploratorio de los datos.
skim(df)
    Data summary
    Name df
    Number of rows 991
    Number of columns 31
    _______________________
    Column type frequency:
    factor 3
    numeric 28
    ________________________
    Group variables None

    Variable type: factor

    skim_variable n_missing complete_rate ordered n_unique top_counts
    Id 0 1 FALSE 991 100: 1, 100: 1, 100: 1, 101: 1
    Ojo 0 1 FALSE 1 I: 991
    Glaucoma 0 1 FALSE 2 No: 765, Sí: 226

    Variable type: numeric

    skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
    AnilloBMO.G 0 1 -0.12 1.38 -4.59 -0.88 -0.04 0.73 4.52 ▁▃▇▃▁
    AnilloBMO.NS 0 1 0.02 1.33 -4.22 -0.79 0.06 0.94 4.57 ▁▃▇▃▁
    AnilloBMO.N 0 1 -0.14 1.30 -4.49 -0.94 -0.05 0.70 4.00 ▁▃▇▅▁
    AnilloBMO.NI 0 1 -0.21 1.23 -4.66 -0.88 -0.16 0.60 3.90 ▁▂▇▅▁
    AnilloBMO.TI 0 1 -0.21 1.37 -4.87 -0.91 -0.16 0.65 4.23 ▁▂▇▃▁
    AnilloBMO.T 0 1 0.02 1.33 -4.05 -0.78 0.02 0.76 6.75 ▁▇▆▁▁
    AnilloBMO.TS 0 1 -0.09 1.40 -4.79 -0.89 -0.02 0.73 5.42 ▁▃▇▂▁
    Anillo3.5.G 0 1 -0.23 1.73 -9.04 -0.85 0.04 0.81 4.85 ▁▁▃▇▁
    Anillo3.5.NS 0 1 0.05 1.21 -4.63 -0.71 0.09 0.85 4.19 ▁▂▇▅▁
    Anillo3.5.N 0 1 0.04 1.28 -5.53 -0.70 0.13 0.86 5.44 ▁▂▇▂▁
    Anillo3.5.NI 0 1 0.08 1.22 -4.58 -0.67 0.08 0.90 4.59 ▁▂▇▃▁
    Anillo3.5.TI 0 1 -0.45 1.74 -7.49 -1.07 -0.24 0.62 4.06 ▁▁▅▇▁
    Anillo3.5.T 0 1 -0.27 1.27 -5.90 -0.99 -0.29 0.44 6.67 ▁▃▇▁▁
    Anillo3.5.TS 0 1 -0.46 1.39 -5.59 -1.19 -0.35 0.46 3.19 ▁▂▇▇▁
    Anillo4.1.G 0 1 -0.24 1.70 -7.30 -0.89 -0.06 0.75 11.25 ▁▇▇▁▁
    Anillo4.1.NS 0 1 0.11 1.25 -4.17 -0.69 0.10 0.90 6.00 ▁▆▇▁▁
    Anillo4.1.N 0 1 0.00 1.34 -5.44 -0.73 0.07 0.82 9.63 ▁▇▃▁▁
    Anillo4.1.NI 0 1 0.10 1.19 -4.33 -0.66 0.10 0.87 7.39 ▁▇▆▁▁
    Anillo4.1.TI 0 1 -0.40 1.69 -6.84 -1.05 -0.24 0.66 4.69 ▁▁▇▆▁
    Anillo4.1.T 0 1 -0.25 1.24 -5.42 -0.95 -0.31 0.41 6.37 ▁▅▇▁▁
    Anillo4.1.TS 0 1 -0.52 1.47 -5.80 -1.23 -0.36 0.44 3.15 ▁▁▆▇▁
    Anillo4.7.G 0 1 -0.21 1.60 -8.62 -0.82 -0.03 0.73 8.16 ▁▁▇▁▁
    Anillo4.7.NS 0 1 0.18 1.30 -4.36 -0.67 0.11 0.99 5.16 ▁▃▇▂▁
    Anillo4.7.N 0 1 -0.02 1.34 -6.76 -0.70 0.03 0.78 9.86 ▁▆▇▁▁
    Anillo4.7.NI 0 1 0.09 1.18 -4.55 -0.68 0.10 0.84 5.24 ▁▃▇▂▁
    Anillo4.7.TI 0 1 -0.30 1.63 -8.09 -0.96 -0.08 0.73 3.77 ▁▁▂▇▁
    Anillo4.7.T 0 1 -0.27 1.31 -5.58 -1.02 -0.38 0.39 10.08 ▁▇▂▁▁
    Anillo4.7.TS 0 1 -0.47 1.45 -6.07 -1.13 -0.28 0.50 2.99 ▁▁▅▇▁

  3. Estudiar la correlación entre las variables numéricas del conjunto de datos.

    library(GGally)
# Seleccionamos las variables numéricas (son las que empiezan por "Anillo").
df |> select(starts_with("Anillo")) |>
    # Diagrama de correlación entre las variables numéricas.
    ggcorr(label = TRUE, label_size = 3)

  4. Calcular los componentes principales del conjunto de variables numéricas y mostrar la varianza explicada por cada componente.

    library(FactoMineR)
# Seleccionamos las variables numéricas (son las que empiezan por "Anillo").
componentes <- df |> select(starts_with("Anillo")) |>
    # Calculamos los componentes principales.
    PCA(graph = FALSE)   

# Mostramos los autovalores y varianza explicada.
kable(componentes$eig)
    eigenvalue percentage of variance cumulative percentage of variance
    comp 1 15.3601308 54.8576099 54.85761
    comp 2 3.6529140 13.0461213 67.90373
    comp 3 2.6718342 9.5422649 77.44600
    comp 4 1.4435284 5.1554584 82.60145
    comp 5 1.2352081 4.4114574 87.01291
    comp 6 1.0625195 3.7947126 90.80762
    comp 7 0.7845921 2.8021148 93.60974
    comp 8 0.3286448 1.1737313 94.78347
    comp 9 0.2663523 0.9512582 95.73473
    comp 10 0.2395828 0.8556527 96.59038
    comp 11 0.1525190 0.5447106 97.13509
    comp 12 0.1329378 0.4747777 97.60987
    comp 13 0.1127224 0.4025801 98.01245
    comp 14 0.0974320 0.3479714 98.36042
    comp 15 0.0722280 0.2579570 98.61838
    comp 16 0.0688993 0.2460689 98.86445
    comp 17 0.0593030 0.2117963 99.07624
    comp 18 0.0542424 0.1937228 99.26997
    comp 19 0.0453290 0.1618892 99.43186
    comp 20 0.0403514 0.1441121 99.57597
    comp 21 0.0371584 0.1327085 99.70868
    comp 22 0.0284767 0.1017025 99.81038
    comp 23 0.0267642 0.0955865 99.90597
    comp 24 0.0248824 0.0888656 99.99483
    comp 25 0.0006527 0.0023312 99.99716
    comp 26 0.0004568 0.0016315 99.99879
    comp 27 0.0003371 0.0012038 100.00000
    comp 28 0.0000008 0.0000027 100.00000 
    # Dibujamos un gráfico de la varianza explicada
library(factoextra)
fviz_eig(componentes, addlabels = TRUE)

  5. Dibujar un diagrama de dispersión de los dos primeros componentes principales coloreando los puntos según el diagnóstico de glaucoma.

    library(plotly)
# Dibujamos el diagrama de dispersión de los dos primeros componentes principales.
plot <- componentes |> fviz_pca_ind(col.ind = df$Glaucoma, label = "none") +
    labs(title = "Gráfico de dispersión de los dos primeros componentes principales",
        x = "Componente Principal 1",
        y = "Componente Principal 2")
ggplotly(plot) # Convertimos el gráfico a interactivo

  6. Realizar un agrupamiento en grupos utilizando el método de las \(k\)-medias y representar los grupos en un diagrama de dispersión.

    # Establecemos una semilla para la reproducibilidad.
set.seed(123)
# Filtramos los datos para quedarnos solo con los pacientes con glaucoma.
df |> filter(Glaucoma == "Sí") |> 
    # Seleccionamos las variables numéricas (son las que empiezan por "Anillo").
    select(starts_with("Anillo")) |>
    # Determinamos el número óptimo de grupos utilizando las distancias dentro de cada grupo al cuadrado.
    fviz_nbclust(kmeans, method = "wss")

    A la vista del gráfico anterior, el número óptimo de grupos, donde se ubica el “codo” del gráfico, sería 3 o 4.

    # Filtramos los datos para quedarnos solo con los pacientes con glaucoma.
agrupacion <- df |> filter(Glaucoma == "Sí") |> 
    # Seleccionamos las variables numéricas (son las que empiezan por "Anillo").
    select(starts_with("Anillo")) |>
    # Realizamos el agrupamiento en 4 grupos.
    kmeans(centers = 4)
# Extraemos los centroides de los grupos y los ordenamos de mayor a menor por la primera componente.    
centroides <- agrupacion$centers[order(agrupacion$centers[,1], decreasing = T),]
# Filtramos de nuevo para quedarnos solo con los pacientes con glaucoma.
agrupacion <- df |> filter(Glaucoma == "Sí") |> 
    # Seleccionamos las variables numéricas (son las que empiezan por "Anillo").
    select(starts_with("Anillo")) |>
    # Volvemos a realizar el agrupamiento en 4 grupos, pero ahora partiendo de los centroides ordenados.
    kmeans(centers = centroides)
# Convertimos los grupos en un factor.
agrupacion$cluster <- as.factor(agrupacion$cluster)
# Asignamos etiquetas a los niveles del factor.
labels <- c("I", "II", "III", "IV")
levels(agrupacion$cluster) <- labels
# Creamos un data frame de los pacientes con glaucoma y le añadimos los grupos.
df_glaucoma <- df |> filter(Glaucoma == "Sí") |> 
    mutate(Estadio = agrupacion$cluster)
# Filtramos el data frame original para quedarnos solo con los pacientes sin glaucoma.
df <- df |> filter(Glaucoma == "No") |> 
    # Añadimos al data frame original una nueva columna con el Estadio de glaucoma.
    mutate(Estadio = "Sano") |> 
    # Unimos los data frames de pacientes con y sin glaucoma.
    bind_rows(df_glaucoma)

# Dibujamos un diagrama de dispersión de los dos primeros componentes principales coloreando los puntos según el estadio de glaucoma. Añadimos elipses alrededor de los grupos.
plot <- componentes |> fviz_pca_ind(col.ind = df$Estadio, label = "none", addEllipses = T) +
    labs(title = "Gráfico de dispersión de los dos primeros componentes principales según estadio de Glaucoma")
ggplotly(plot)

3.2 Ejercicios propuestos

Ejercicio 3.3 El conjunto de datos cancer-mama.csv contiene información sobre las características de núcleos de células mamarias obtenidas de imágenes digitalizadas tanto de células cancerosas como no cancerosas obtenidas por biopsia. Las variables que contiene son:

  • ID: Identificador único de la muestra.
  • Diagnóstico: Diagnóstico de la muestra (M: maligno, B: benigno).
  • Radio: Media de la distancia desde el centro hasta los puntos de la superficie.
  • Textura: Desviación estándar de la intensidad de gris de los puntos.
  • Perímetro: Longitud del contorno.
  • Área: Área de la imagen.
  • Suavidad: Variación local en la longitud del radio.
  • Compacidad: Perímetro^2 / Área - 1.0.
  • Concavidad: Magnitud de las porciones cóncavas del contorno.
  • Puntos_concavos: Número de puntos cóncavos del contorno.
  • Simetría: Simetría de la imagen.
  • Irregularidad: Medida de la irregularidad de la forma.

  1. Crear un dataframe con los datos del archivo cancer-mama.csv.

  2. Realizar un análisis exploratorio de los datos.

  3. Dibujar un diagrama de correlación entre las variables numéricas del conjunto de datos.

  4. Calcular los componentes principales del conjunto de variables numéricas.

  5. Dibujar un diagrama de barras con la varianza explicada por cada componente principal.

  6. Dibujar un diagrama de dispersión de los dos primeros componentes principales coloreando los puntos según el diagnóstico.

  7. Realizar un agrupamiento en grupos utilizando el método de las \(k\)-medias y representar los grupos en un diagrama de dispersión.

Ejercicio 3.4 El fichero vinos.csv contiene información sobre las características de vinos blancos y tintos portugueses de la denominación “Vinho Verde”. Las variables que contiene son las siguientes:

Variable Descripción Tipo (unidades)
tipo Tipo de vino Factor (blanco, tinto)
meses.barrica Meses de envejecimiento en barrica Numérica(meses)
acided.fija Cantidad de ácidotartárico Numérica(g/dm3)
acided.volatil Cantidad de ácido acético Numérica(g/dm3)
acido.citrico Cantidad de ácidocítrico Numérica(g/dm3)
azucar.residual Cantidad de azúcar remanente después de la fermentación Numérica(g/dm3)
cloruro.sodico Cantidad de clorurosódico Numérica(g/dm3)
dioxido.azufre.libre Cantidad de dióxido de azufre en forma libre Numérica(mg/dm3)
dioxido.azufre.total Cantidad de dióxido de azufre total en forma libre o ligada Numérica(mg/dm3)
densidad Densidad Numérica(g/cm3)
ph pH Numérica(0-14)
sulfatos Cantidad de sulfato de potasio Numérica(g/dm3)
alcohol Porcentaje de contenido de alcohol Numérica(0-100)
calidad Calificación otorgada por un panel de expertos Numérica(0-10)

  1. Crear un dataframe con los datos del archivo vinos.csv.

  2. Realizar un análisis exploratorio de los datos.

  3. Dibujar un diagrama de correlación entre las variables numéricas del conjunto de datos.

  4. Calcular los componentes principales del conjunto de variables numéricas químicas.

  5. Dibujar un diagrama de barras con la varianza explicada por cada componente principal.

  6. Dibujar un diagrama de dispersión de los dos primeros componentes principales coloreando los puntos según el tipo de vino. Repetir el diagrama de dispersión coloreando los puntos según el envejecimiento del vino.

  7. Realizar un agrupamiento en grupos utilizando el método de las \(k\)-medias y representar los grupos en un diagrama de dispersión.