4 Regresión

El aprendizaje supervisado abarca técnicas para clasificar o predecir una variable respuesta a partir de un conjunto de variables predictivas. Los modelos de aprendizaje basados en regresión son modelos bastante simples que pueden utilizarse para predecir variables cuantitativas (regresión lineal o no lineal) o cualitativas (regresión logística). Esta práctica contiene ejercicios que muestran como construir modelos de aprendizaje de regresión lineal, no lineal y regresión logística con R y el paquete tidymodels.

4.1 Ejercicios Resueltos

Para la realización de esta práctica se requieren los siguientes paquetes:

library(tidyverse) 
# Incluye los siguientes paquetes:
# - readr: para la lectura de ficheros csv. 
# - dplyr: para el preprocesamiento y manipulación de datos.
# - ggplot2: para la visualización de datos.
library(tidymodels)
# Incluye los siguientes paquetes:
# - recipes: para la preparación de los datos. 
# - parsnip: para la creación de modelos.
# - workflows: para la creación de flujos de trabajo.
# - rsample: para la creación de particiones de los datos.
# - yardstick: para la evaluación de modelos.
# - tune: para la optimización de hiperparámetros.
library(skimr) # para el análisis exploratorio de datos.
library(GGally) # para la visualización de matrices de correlación.
library(plotly) # para la visualización interactiva de gráficos.
library(knitr) # para el formateo de tablas.

Ejercicio 4.1 El conjunto de datos medidas-fisicas.csv contiene un conjunto de datos con la edad, sexo, estatura (cm), peso (kg) y el deporte que hacen una muestra de personas (días a la semana).

Cargar los datos del archivo medidas-fisicas.csv en un data frame.

Solución

library(tidyverse)
# Cargamos los datos del fichero CSV en un data frame.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/medidas-fisicas.csv", stringsAsFactors = TRUE)
# Mostramos un resumen de los datos.
glimpse(df)

Rows: 6,779
Columns: 5
$ Edad        <int> 34, 4, 49, 9, 8, 45, 66, 58, 54, 10, 58, 50, 9, 33, 60, 16…
$ Sexo        <fct> hombre, hombre, mujer, hombre, hombre, mujer, hombre, homb…
$ Estatura    <dbl> 164.7, 105.4, 168.4, 133.1, 130.6, 166.7, 169.5, 181.9, 16…
$ Peso        <dbl> 87.4, 17.0, 86.7, 29.8, 35.2, 67.7, 56.7, 69.8, 73.1, 38.6…
$ DiasDeporte <int> 0, 0, 0, 0, 0, 5, 7, 5, 1, 0, 2, 7, 0, 0, 0, 3, 7, 3, 3, 0…

Realizar un análisis exploratorio de los datos.

Solución

library(skimr)
# Realizamos un análisis exploratorio de los datos.
skim(df)

Data summary
Name	df
Number of rows	6779
Number of columns	5
_______________________
Column type frequency:
factor	1
numeric	4
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
Sexo	0	1	FALSE	2	muj: 3420, hom: 3359

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Edad	0	1.00	35.45	23.12	0.0	15.0	34.0	54.00	80.0	▇▆▆▅▅
Estatura	298	0.96	160.35	21.13	83.6	155.4	165.1	173.70	200.4	▁▁▂▇▂
Peso	55	0.99	66.08	29.90	-7.9	49.4	67.9	84.73	230.7	▂▇▃▁▁
DiasDeporte	0	1.00	1.70	2.24	0.0	0.0	0.0	3.00	7.0	▇▁▂▁▁

Preprocesar el conjunto de datos filtrando las personas mayores de edad y eliminando las filas con con datos perdidos.

Solución

# Filtramos las personas mayores de edad.
df <- df  |> filter(Edad >= 18)  |> 
    # Eliminamos las filas con datos perdidos.
    drop_na()

Dibujar un diagrama de relación entre todos los pares de variables del conjunto de datos diferenciando por el sexo de las personas.

Ayuda

Se puede utilizar la función ggpairs del paquete GGally para dibujar un diagrama de relación entre todos los pares de variables del conjunto de datos. Asociar el sexo a la dimensión del color.
Solución
library(GGally) # Dibujamos un diagrama de relación entre todos los pares de variables del conjunto de datos diferenciando por el sexo. ggpairs(df, aes(color = Sexo, alpha = 0.5))
Descomponer el conjunto de datos en un subconjunto de entrenamiento con el 80% de los datos y un subconjunto de test con el 20% restante.
Ayuda
Utilizar la función initial_split del paquete rsample para dividir el conjunto de datos en entrenamiento y test.
Parámetros:
- data: el data frame con los datos.
- prop: la proporción del conjunto de datos que se utilizará para el conjunto de entrenamiento (en este caso, 0.8 para el 80%).
Solución
library(tidymodels) # Establecemos una semilla aleatoria para la reproducibilidad. set.seed(123) # Dividimos el conjunto de datos en entrenamiento (80%) y test (20%). df_particion <- initial_split(df, prop = 0.8) # Extraemos el conjunto de datos de entrenamiento. df_entrenamiento <- training(df_particion) # Extraemos el conjunto de datos de test. df_test <- testing(df_particion)

Dibujar el diagrama de dispersión de la estatura y el peso.

Solución

# Dibujamos el diagrama de dispersión de la estatura y el peso.
diagrama_dispersion <- ggplot(df_entrenamiento, aes(x = Estatura, y = Peso)) +
  geom_point() +
  labs(title = "Diagrama de dispersión de Estatura y Peso")
diagrama_dispersion

Construir un modelo de regresión lineal para predecir el peso en función de la estatura.

Ayuda

Utilizar la función lm del paquete base para crear un modelo de regresión lineal con la fórmula Peso ~ Estatura para indicar que el peso es la variable dependiente y la estatura es la variable independiente.

O bien, utilizar la función linear_reg del paquete tidymodels para crear un modelo de regresión lineal y usar la función set_engine para establecer el motor de cálculo como “lm” (mínimos cuadrados). Una vez definido el tipo de modelo, utilizar la función fit para ajustar el modelo a los datos, pasándole la fórmula Peso ~ Estatura para indicar que el peso es la variable dependiente y la estatura es la variable independiente.
Solución
Base
Tidymodels

library(knitr) # Creamos un modelo de regresión lineal. modelo <- lm(Peso ~ Estatura, data = df_entrenamiento) # Mostramos un resumen del modelo. tidy(modelo) |> kable()

term estimate std.error statistic p.value

(Intercept) -69.3115840 5.4317717 -12.7604 0

Estatura 0.8799128 0.0322225 27.3074 0

library(knitr) # Creamos un modelo de regresión lineal. modelo <- linear_reg() |> # Establecemos como motor de cálculo el ajuste por mínimos cuadrados. set_engine("lm") |> # Establecemos el modo del modelo como regresión. set_mode("regression") modelo_entrenado <- modelo |> # Entrenamos el modelo con los datos de entrenamiento. fit(Peso ~ Estatura, data = df_entrenamiento) # Mostramos un resumen del modelo. tidy(modelo_entrenado) |> kable()

term estimate std.error statistic p.value

(Intercept) -69.3115840 5.4317717 -12.7604 0

Estatura 0.8799128 0.0322225 27.3074 0

term	estimate	std.error	statistic	p.value
(Intercept)	-69.3115840	5.4317717	-12.7604	0
Estatura	0.8799128	0.0322225	27.3074	0

term	estimate	std.error	statistic	p.value
(Intercept)	-69.3115840	5.4317717	-12.7604	0
Estatura	0.8799128	0.0322225	27.3074	0

Dibujar el modelo de regresión lineal sobre el diagrama de dispersión de la estatura y el peso.

Solución

# Dibujamos el modelo de regresión lineal sobre el diagrama de dispersión de la estatura y el peso.
diagrama_dispersion + geom_smooth(method = "lm")

Predecir el peso de las personas del conjunto de test utilizando el modelo de regresión lineal ajustado.

Ayuda

Utilizar la función predict del paquete base para predecir el peso de las personas del conjunto de test. Pasar el modelo ajustado y el conjunto de datos de test como argumentos.

Parámetros:

new_data: el conjunto de datos de test.

O bien usar la función augment del paquete parsnip para añadir al conjunto de test las probabilidades cada especie de pingüino.

Parámetros:

new_data: el conjunto de datos de test.

Solución

Base
Tidymodels

# Añadimos al conjunto de datos de test las predicciones del peso según el modelo ajustado.
df_test <- df_test |>
    mutate(Peso_Predicho = predict(modelo_entrenado, new_data = df_test)$.pred)  
head(df_test) |> kable()

Edad	Sexo	Estatura	Peso	DiasDeporte	Peso_Predicho
54	hombre	169.4	73.1	1	79.74564
50	hombre	177.8	71.5	7	87.13690
33	hombre	181.3	93.8	0	90.21660
37	mujer	154.8	42.9	5	66.89891
28	mujer	169.6	134.3	0	79.92162
30	hombre	175.8	88.4	0	85.37708

# Añadimos al conjunto de datos de test las predicciones del peso según el modelo ajustado.
modelo_entrenado |> augment(new_data = df_test) |> 
    head() |> 
    kable()

.pred	.resid	Edad	Sexo	Estatura	Peso	DiasDeporte	Peso_Predicho
79.74564	-6.645638	54	hombre	169.4	73.1	1	79.74564
87.13690	-15.636905	50	hombre	177.8	71.5	7	87.13690
90.21660	3.583400	33	hombre	181.3	93.8	0	90.21660
66.89891	-23.998911	37	mujer	154.8	42.9	5	66.89891
79.92162	54.378380	28	mujer	169.6	134.3	0	79.92162
85.37708	3.022921	30	hombre	175.8	88.4	0	85.37708

Dibujar los errores predictivos entre el peso real y el peso predicho en el conjunto de datos de test.

Solución

# Dibujamos los errores predictivos entre el peso real y el peso predicho en el conjunto de datos de test.
ggplot(df_test, aes(x = Peso, y = Peso_Predicho)) +
  geom_abline(slope = 1, intercept = 0, color = "red") +
  geom_point() +
  geom_segment(aes(xend = Peso, yend = Peso), color = "blue", alpha = 0.5) +
  labs(title = "Errores predictivos (líneas verticales) entre Peso Real y Predicho",
       x = "Peso Real",
       y = "Peso Predicho")

Evaluar el modelo de regresión lineal calculando el error cuadrático medio (RMSE) y el coeficiente de determinación (\(R^2\)).
Ayuda
Usar la función metrics del paquete yardstick para calcular las métricas de evaluación del modelo.
Parámetros:
- truth: la variable respuesta (en este caso, Especie).
- estimate: la variable con las predicciones modelo (en este caso, Peso_Predicho).
Solución
# Evaluamos el modelo de regresión lineal calculando el error cuadrático medio (RMSE) y el coeficiente de determinación (R^2). df_test |> metrics(truth = Peso, estimate = Peso_Predicho) |> kable()

.metric .estimator .estimate

rmse standard 19.1912493

rsq standard 0.1715209

mae standard 14.9523600

.metric	.estimator	.estimate
rmse	standard	19.1912493
rsq	standard	0.1715209
mae	standard	14.9523600

Incluir en el modelo de regresión lineal la variable sexo como variable categórica y volver a ajustar el modelo.

Solución

# Creamos otro modelo de regresión lineal añadiendo al modelo anterior la variable predictiva Sexo.
modelo_entrenado_sexo <- modelo |>
    # Ajustamos el nuevo modelo con los datos del conjunto de entrenamiento.
    fit(Peso ~ Estatura * Sexo, data = df_entrenamiento)

# Mostramos un resumen del nuevo modelo.
tidy(modelo_entrenado_sexo) |> 
    kable()

term	estimate	std.error	statistic	p.value
(Intercept)	-94.2039913	10.8315382	-8.697194	0.0000000
Estatura	1.0211716	0.0617002	16.550548	0.0000000
Sexomujer	43.6315911	14.7870144	2.950669	0.0031901
Estatura:Sexomujer	-0.2565078	0.0876188	-2.927545	0.0034367

Dibujar el modelo de regresión lineal con la variable sexo sobre el diagrama de dispersión de la estatura y el peso.

Solución

# Dibujamos el modelo de regresión lineal con la variable sexo sobre el diagrama de dispersión de la estatura y el peso.
df_entrenamiento  |> ggplot(aes(x = Estatura, y = Peso, color = Sexo)) +
    geom_point() +
    geom_smooth(method = "lm")

    labs(title = "Diagrama de dispersión de Estatura y Peso según Sexo")

$title
[1] "Diagrama de dispersión de Estatura y Peso según Sexo"

attr(,"class")
[1] "labels"

Predecir el peso de las personas del conjunto de test utilizando el modelo de regresión lineal ajustado con la variable sexo y evaluar el nuevo modelo de regresión lineal calculando el error cuadrático medio (RMSE) y el coeficiente de determinación (\(R^2\)). ¿Qué conclusiones puedes sacar de la comparación entre los dos modelos?
Solución
# Añadimos al conjunto de datos de test las predicciones del peso según el nuevo modelo ajustado. modelo_entrenado_sexo |> augment(new_data = df_test) |> # Calculamos las métricas de evaluación del nuevo modelo. metrics(truth = Peso, estimate = .pred) |> kable()

.metric .estimator .estimate

rmse standard 19.1858999

rsq standard 0.1720853

mae standard 14.9409558
El error cuadrático medio no ha disminuido, por lo que la inclusión de la variable sexo no ha mejorado el modelo.

.metric	.estimator	.estimate
rmse	standard	19.1858999
rsq	standard	0.1720853
mae	standard	14.9409558

Construir un nuevo modelo que explique el peso en función de la estatura y el deporte que practican las personas.

Solución

# Creamos un nuevo modelo de regresión lineal añadiendo al modelo inicial la variable predictiva DiasDeporte.
modelo_entrenado_deporte <- modelo |>
    # Ajustamos el nuevo modelo con los datos del conjunto de entrenamiento.
    fit(Peso ~ Estatura + DiasDeporte, data = df_entrenamiento)

# Mostramos un resumen del nuevo modelo.
tidy(modelo_entrenado_deporte) |> 
    kable()

term	estimate	std.error	statistic
(Intercept)	-69.7060760	5.2092631	-13.38118
Estatura	0.9091978	0.0309437	29.38234
DiasDeporte	-2.5440654	0.1390180	-18.30026

Dibujar el modelo de regresión lineal con la variable deporte sobre el diagrama de dispersión de la estatura y el peso.

Solución

# Dibujamos el modelo de regresión lineal con la variable deporte sobre el diagrama de dispersión de la estatura y el peso.
df_entrenamiento  |> ggplot(aes(x = Estatura, y = Peso, color = DiasDeporte)) +
    geom_point() +
    geom_smooth(method = "lm") +
    labs(title = "Diagrama de dispersión de Estatura y Peso según Días de Deporte")

Evaluar el nuevo modelo de regresión lineal calculando el error cuadrático medio (RMSE) y el coeficiente de determinación (\(R^2\)). ¿Qué conclusiones puedes sacar ahora?
Solución
# Añadimos al conjunto de datos de test las predicciones del peso según el nuevo modelo ajustado. modelo_entrenado_deporte |> augment(new_data = df_test) |> # Calculamos las métricas de evaluación del nuevo modelo. metrics(truth = Peso, estimate = .pred) |> kable()

.metric .estimator .estimate

rmse standard 18.4424646

rsq standard 0.2351604

mae standard 14.3124504
El error cuadrático medio ha disminuido un poco, pero aún así la inclusión de la variable deporte no ha mejorado mucho el modelo.

.metric	.estimator	.estimate
rmse	standard	18.4424646
rsq	standard	0.2351604
mae	standard	14.3124504

Ejercicio 4.2 El fichero dieta.csv contiene información sobre el los kilos perdidos con una dieta de adelgazamiento.

Crear un data frame con los datos de la dieta a partir del fichero dieta.csv.

Solución

library(tidyverse)
# Cargamos los datos del fichero CSV en un data frame.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/dieta.csv", stringsAsFactors = TRUE)
# Mostramos un resumen de los datos.
glimpse(df)

Rows: 40
Columns: 3
$ dias         <int> 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62, 66, 7…
$ peso_perdido <dbl> 2.95, 5.65, 6.56, 3.56, 6.17, 9.40, 12.35, 12.93, 13.94, …
$ ejercicio    <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…

Dibujar el diagrama de dispersión de los kilos perdidos en función del número de días con la dieta. ¿Qué tipo de modelo de regresión se ajusta mejor a la nube de puntos?

Solución

# Dibujamos el diagrama de dispersión de los kilos perdidos en función del número de días con la dieta.
ggplot(df, aes(x = dias, y = peso_perdido)) +
    geom_point() +
    labs(title = "Diagrama de dispersión del peso perdido y los días de dieta", x = "Días de dieta", y = "Peso perdido en Kg")

La nube de puntos es bastante difusa aunque parece apreciarse una tendencia logarítmica o sigmoidal.

Dividir el conjunto de datos en un subconjunto de entrenamiento con el 75% de los datos y un subconjunto de test con el 25% restante.

Solución

library(tidymodels)
# Establecemos una semilla aleatoria para la reproducibilidad.
set.seed(123) 
# Dividimos el conjunto de datos en entrenamiento (75%) y test (25%)
df_particion <- initial_split(df, prop = 0.75)
# Extraemos el conjunto de datos de entrenamiento.
df_entrenamiento <- training(df_particion)
# Extraemos el conjunto de datos de test.
df_test <- testing(df_particion)

Ajustar un modelo de regresión sigmoidal a los datos de la dieta y evaluarlo mediante validación cruzada con 5 pliegues.

Solución

library(knitr)
# Definimos el modelo de regresión lineal.
modelo <- linear_reg() |> 
    # Establecemos como motor de cálculo el ajuste por mínimos cuadrados.
    set_engine("lm") 

# Establecemos una semilla aleatoria para la reproducibilidad.
set.seed(123)
# Definimos el conjunto de validación mediante validación cruzada con 10 pliegues.
df_cv <- vfold_cv(df_entrenamiento, v = 5)

# Creamos un flujo de trabajo para entrenar el modelo.
workflow() |>
    # Añadimos el modelo de regresión lineal.
    add_model(modelo) |> 
    # Añadimos la fórmula del modelo de regresión sigmoidal.
    add_formula(log(peso_perdido) ~ I(1/dias))  |>
    # Añadimos el conjunto de datos de validación.
    fit_resamples(resamples = df_cv)  |>
    # Calculamos las métricas de evaluación del modelo.
    collect_metrics() |> 
    kable()

.metric	.estimator	mean	n	std_err	.config
rmse	standard	0.3263752	5	0.0416058	Preprocessor1_Model1
rsq	standard	0.5761779	5	0.1606296	Preprocessor1_Model1

Ajustar un modelo de regresión inverso a los datos de la dieta y evaluarlo mediante validación cruzada con 5 pliegues.

Solución

workflow() |> 
    # Añadimos el modelo de regresión lineal.
    add_model(modelo) |> 
    # Añadimos la fórmula del modelo de regresión inverso.
    add_formula(peso_perdido ~ I(1/dias))  |>
    # Añadimos el conjunto de datos de validación.
    fit_resamples(resamples = df_cv)  |>
    # Calculamos las métricas de evaluación del modelo.
    collect_metrics() |> 
    kable()

.metric	.estimator	mean	n	std_err	.config
rmse	standard	3.5477148	5	0.3300098	Preprocessor1_Model1
rsq	standard	0.6146749	5	0.0458547	Preprocessor1_Model1

Ajustar un modelo de regresión potencial a los datos de la dieta y evaluarlo mediante validación cruzada con 5 pliegues.

Solución

workflow() |> 
    # Añadimos el modelo de regresión lineal.
    add_model(modelo) |> 
    # Añadimos la fórmula del modelo de regresión potencial.
    add_formula(log(peso_perdido) ~ log(dias))  |>
    # Añadimos el conjunto de datos de validación.
    fit_resamples(resamples = df_cv)  |>
    # Calculamos las métricas de evaluación del modelo.
    collect_metrics() |> 
    kable()

.metric	.estimator	mean	n	std_err	.config
rmse	standard	0.3410319	5	0.0432541	Preprocessor1_Model1
rsq	standard	0.6952170	5	0.0312989	Preprocessor1_Model1

Ejercicio 4.3 El fichero infartos.csv contiene información sobre distintas variables fisiológicas relacionadas con el riesgo de infarto de una muestra de personas. Las variables que contienen son:

Edad: Edad del paciente (años)
Sexo: Sexo del paciente (H: hombre, M: mujer)
DolorPecho: Tipo de dolor torácico (TA: angina típica, ATA: angina atípica, NAP: dolor no anginoso, ASY: asintomático)
PresionArterial: Presión arterial sistólica en reposo (mm Hg)
Colesterol: Colesterol sérico (mm/dl)
Glucemia: Glucemia en ayunas (1: si glucemia en ayunas > 120 mg/dl, 0: de lo contrario)
Electro: resultados del electrocardiograma en reposo (Normal: normal, ST: anomalía onda ST-T (inversiones de onda T y/o elevación o depresión de ST > 0,05 mV), LVH: hipertrofia ventricular izquierda probable o definitiva según criterios de Estes)
Pulsaciones: Frecuencia cardíaca máxima alcanzada (valor numérico entre 60 y 202)
AnginaEjercicio: Angina inducida por ejercicio (S: sí, N: no)
DepresionST: Depresión del segmento ST inducida por el ejercicio (valor numérico de la depresión).
PendienteST: Pendiente del segmento ST en el pico de ejercicio (Ascendente, Plano, Descencdente).
Infarto: Riesgo de infarto (1: Sí, 0: No)

Cargar los datos del archivo infartos.csv en un data frame.

Solución

library(tidyverse)
# Cargamos los datos del fichero CSV en un data frame.
df <- read.csv("https://aprendeconalf.es/aprendizaje-automatico-practicas-r/datos/infartos.csv", stringsAsFactors = TRUE)
# Mostramos un resumen de los datos.
glimpse(df)

Rows: 918
Columns: 12
$ Edad            <int> 40, 49, 37, 48, 54, 39, 45, 54, 37, 48, 37, 58, 39, 49…
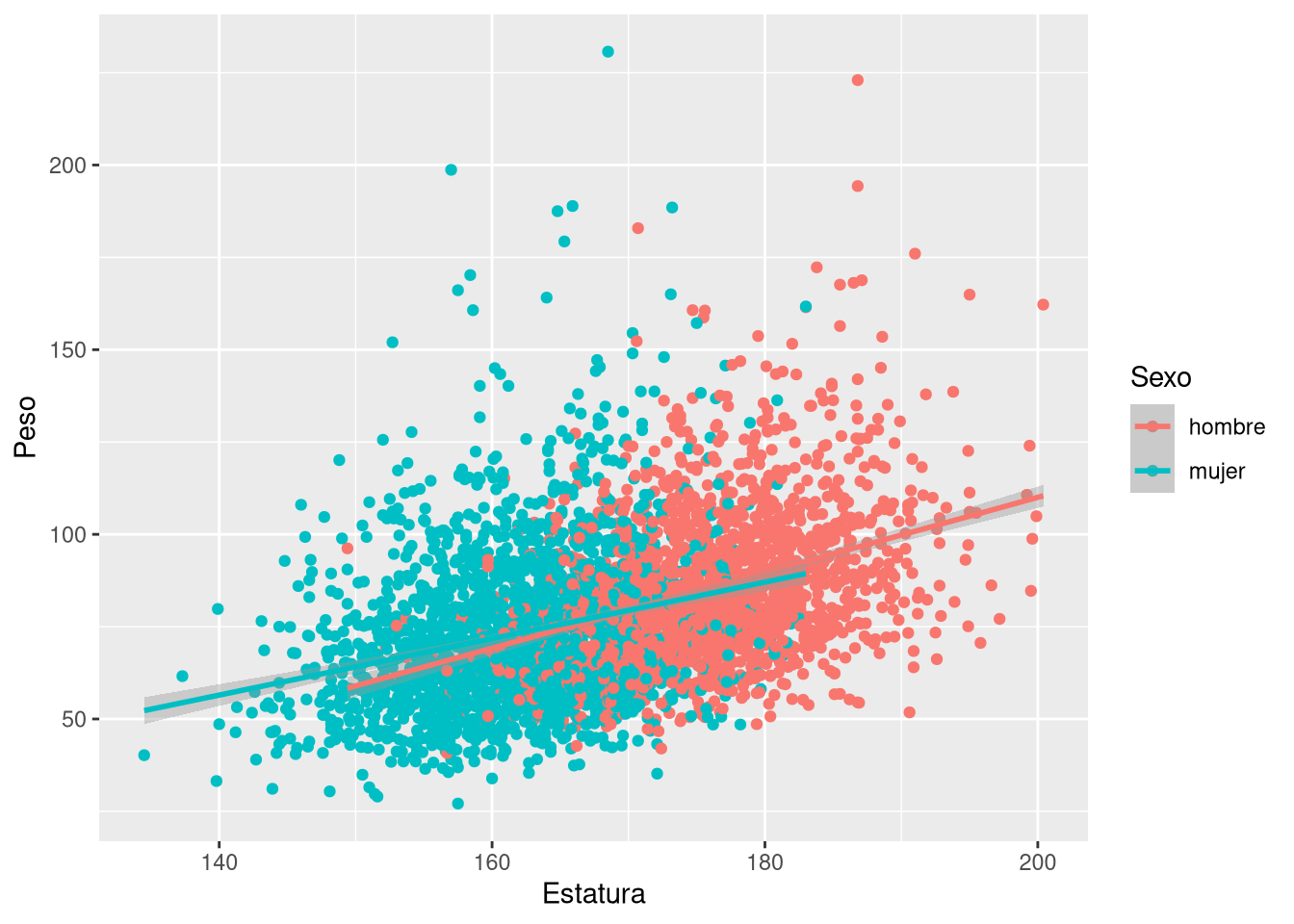
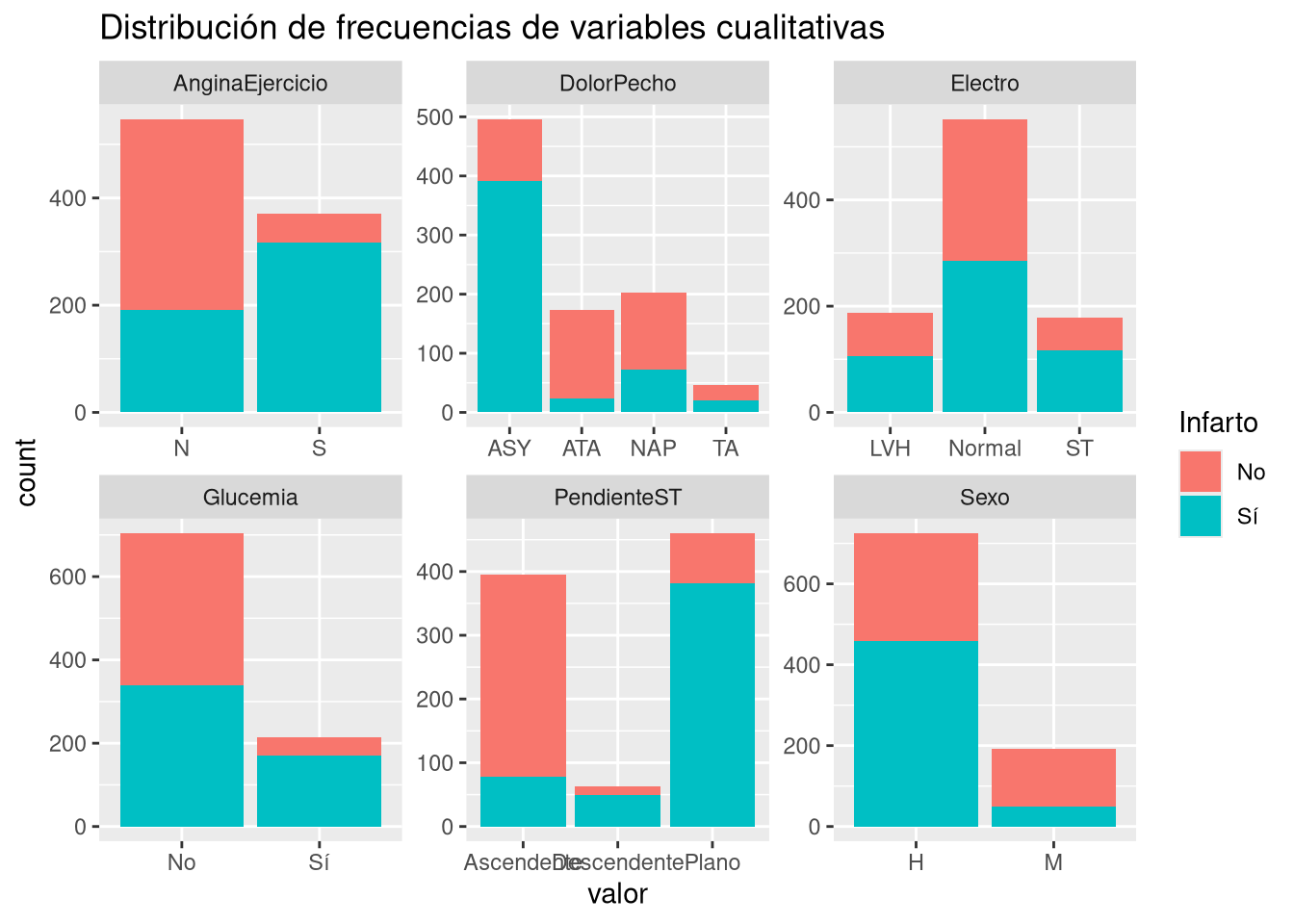
$ Sexo            <fct> H, M, H, M, H, H, M, H, H, M, M, H, H, H, M, M, H, M, …
$ DolorPecho      <fct> ATA, NAP, ATA, ASY, NAP, NAP, ATA, ATA, ASY, ATA, NAP,…
$ PresionArterial <int> 140, 160, 130, 138, 150, 120, 130, 110, 140, 120, 130,…
$ Colesterol      <int> 289, 180, 283, 214, 195, 339, 237, 208, 207, 284, 211,…
$ Glucemia        <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ Electro         <fct> Normal, Normal, ST, Normal, Normal, Normal, Normal, No…
$ Pulsaciones     <int> 172, 156, 98, 108, 122, 170, 170, 142, 130, 120, 142, …
$ AnginaEjercicio <fct> N, N, N, S, N, N, N, N, S, N, N, S, N, S, N, N, N, N, …
$ DepresionST     <dbl> 0.0, 1.0, 0.0, 1.5, 0.0, 0.0, 0.0, 0.0, 1.5, 0.0, 0.0,…
$ PendienteST     <fct> Ascendente, Plano, Ascendente, Plano, Ascendente, Asce…
$ Infarto         <int> 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, …

Convertir las variables cualitativas en factores.

Solución

# Convertimos las variables Infarto y Glucemia en factores.
df <- df |> mutate(Infarto = factor(Infarto, levels = c("0", "1"), labels = c("No", "Sí")),
    Glucemia = factor(Glucemia, levels = c("0", "1"), labels = c("No", "Sí")))

Realizar un análisis exploratorio de los datos.

Solución

library(skimr)
# Realizamos un análisis exploratorio de los datos.
skim(df)

Data summary
Name	df
Number of rows	918
Number of columns	12
_______________________
Column type frequency:
factor	7
numeric	5
________________________
Group variables	None

Variable type: factor

skim_variable	complete_rate	ordered	n_unique	top_counts
Sexo	1	FALSE	2	H: 725, M: 193
DolorPecho	1	FALSE	4	ASY: 496, NAP: 203, ATA: 173, TA: 46
Glucemia	1	FALSE	2	No: 704, Sí: 214
Electro	1	FALSE	3	Nor: 552, LVH: 188, ST: 178
AnginaEjercicio	1	FALSE	2	N: 547, S: 371
PendienteST	1	FALSE	3	Pla: 460, Asc: 395, Des: 63
Infarto	1	FALSE	2	Sí: 508, No: 410

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Edad	1	53.51	9.43	28.0	47.00	54.0	60.0	77.0	▁▅▇▆▁
PresionArterial	1	132.40	18.51	0.0	120.00	130.0	140.0	200.0	▁▁▃▇▁
Colesterol	1	198.80	109.38	0.0	173.25	223.0	267.0	603.0	▃▇▇▁▁
Pulsaciones	1	136.81	25.46	60.0	120.00	138.0	156.0	202.0	▁▃▇▆▂
DepresionST	1	0.89	1.07	-2.6	0.00	0.6	1.5	6.2	▁▇▆▁▁

Dibujar un diagrama de relación entre todos los pares de variables del conjunto de datos diferenciando por el riesgo de infarto.
Solución
library(GGally) df |> ggpairs(aes(color = Infarto, alpha = 0.5))

Dibujar los diagramas de barras con la distribución de frecuencias de las variables cualitativas según el riesgo de infarto.

Solución

# Seleccionamos los factores.
df |> select(where(is.factor)) |> 
    # Convertimos el data frame en formato largo.
    pivot_longer(cols = where(is.factor) & !all_of("Infarto"), names_to = "variable", values_to = "valor") |> 
    # Dibujamos el diagrama de barras de las variables cualitativas coloreando según el riesgo de infarto.
    ggplot(aes(x = valor, fill = Infarto)) +
    # Separamos los diagramas para cada variable.
    facet_wrap(~ variable, scales = "free") +
    geom_bar() +
    labs(title = "Distribución de frecuencias de variables cualitativas")

Dibujar los diagramas de cajas de las variables numéricas según el riesgo de infarto.

Solución

# Seleccionamos las variables numéricas.
df |> select(Infarto, where(is.numeric)) |>
    # Convertimos el data frame en formato largo. 
    pivot_longer(cols = where(is.numeric), names_to = "variable", values_to = "valor") |>
    # Dibujamos el diagrama de cajas de las variables numéricas coloreando según el riesgo de infarto.
    ggplot(aes(x = Infarto, y = valor, fill = Infarto)) +
    geom_boxplot() +
    # Separamos los diagramas para cada variable.
    facet_wrap(~ variable, scales = "free") +
    labs(title = "Diagramas de cajas de las variables numéricas según Infarto")

Dibujar un diagrama de correlación entre las variables numéricas del conjunto de datos.
Ayuda
Utilizar la función ggcorr del paquete GGally para dibujar un diagrama de correlación entre las variables numéricas del conjunto de datos.
Parámetros:
- label = TRUE para mostrar las etiquetas de correlación.
Solución
# Seleccionamos las variables numéricas. df |> select_if(is.numeric) |> # Dibujamos el diagrama de correlación entre las variables numéricas. ggcorr(label = TRUE, label_size = 5)

Descomponer el conjunto de datos en un subconjunto de entrenamiento con el 80% de los datos y un subconjunto de test con el 20% restante.

Solución

library(tidymodels)
# Establecemos una semilla aleatoria para la reproducibilidad.
set.seed(123)
# Dividimos el conjunto de datos en entrenamiento (80%) y test (20%) estratificando por la variable Infarto.
df_particion <- initial_split(df, prop = 0.8, strata = "Infarto")
# Extraemos el conjunto de datos de entrenamiento.
df_entrenamiento <- training(df_particion)
# Extraemos el conjunto de datos de test.   
df_test <- testing(df_particion)

Preprocesar el conjunto de datos de entrenamiento para eliminar las variables numéricas con alta correlación, normalizar las variables numéricas y crear variables dummy para las variables categóricas.

Ayuda

Utilizar la función recipe del paquete recipes incluido en la colección de paquetes tidymodels para crear una receta de preprocesamiento.

Parmámetros:

Infarto ~. para indicar que la variable Especie es la variable respuesta y se deben utilizar todas las demás variables como predictivas.

Después, utilizar la función step_normalize para normalizar las variables numéricas.

Parámetros:

all_numeric_predictors() para indicar que se deben utilizar todas las variables numéricas.

Y usar también la función step_dummy para crear variables dummy para las variables categóricas.

Parámetros:

all_nominal_predictors() para indicar que se deben utilizar todas las variables categóricas.

Solución

# Creamos una receta de preprocesamiento para el conjunto de datos de entrenamiento indicando que la variable respuesta es Infarto y las variables predictivas todas las demás.
receta <- recipe(Infarto ~ ., data = df_entrenamiento) |> 
    # Eliminamos las variables numéricas con alta correlación para evitar colinealidad.
    step_corr(all_numeric_predictors(), threshold = 0.8) |> 
    # Normalizamos las variables predictivas numéricas.
    step_normalize(all_numeric_predictors()) |> 
    # Creamos variables dummy para las variables categóricas.
    step_dummy(all_nominal_predictors()) 
summary(receta)

# A tibble: 12 × 4
   variable        type      role      source  
   <chr>           <list>    <chr>     <chr>   
 1 Edad            <chr [2]> predictor original
 2 Sexo            <chr [3]> predictor original
 3 DolorPecho      <chr [3]> predictor original
 4 PresionArterial <chr [2]> predictor original
 5 Colesterol      <chr [2]> predictor original
 6 Glucemia        <chr [3]> predictor original
 7 Electro         <chr [3]> predictor original
 8 Pulsaciones     <chr [2]> predictor original
 9 AnginaEjercicio <chr [3]> predictor original
10 DepresionST     <chr [2]> predictor original
11 PendienteST     <chr [3]> predictor original
12 Infarto         <chr [3]> outcome   original

Ajustar un modelo de regresión logística a los datos de entrenamiento utilizando la receta de preprocesamiento definida anteriormente.

Ayuda

Usar la función logistic_reg del paquete parsnip para crear un modelo de regresión logística y establecer el motor de cálculo como “glm” (máxima verosimilitud) y el modo de clasificación para que devuelva la clase predicha.

Solución

library(knitr)
# Definimos el modelo de regresión logística.
modelo <- logistic_reg() |>
    # Establecemos como motor de cálculo el ajuste por máxima verosimilitud. 
    set_engine("glm") |>
    # Establecemos el modo del modelo como clasificación.
    set_mode("classification") 

# Creamos un flujo de trabajo para entrenar el modelo.
modelo_entrenado <- workflow() |> 
    # Añadimos la receta de preprocesamiento.
    add_recipe(receta) |> 
    # Añadimos el modelo de regresión logística.
    add_model(modelo) |>
    # Entrenamos el modelo a los datos de entrenamiento.
    fit(data = df_entrenamiento) 

tidy(modelo_entrenado) |> 
kable()

term	estimate	std.error	statistic	p.value
(Intercept)	0.0445124	0.3287908	0.1353820	0.8923099
Edad	0.1411774	0.1392874	1.0135688	0.3107886
PresionArterial	0.0558248	0.1230773	0.4535754	0.6501345
Colesterol	-0.4652817	0.1331610	-3.4941296	0.0004756
Pulsaciones	-0.1118208	0.1405529	-0.7955778	0.4262775
DepresionST	0.4001500	0.1409236	2.8394806	0.0045187
Sexo_M	-1.4845959	0.3087981	-4.8076586	0.0000015
DolorPecho_ATA	-1.7750427	0.3498923	-5.0731123	0.0000004
DolorPecho_NAP	-1.7982335	0.2977537	-6.0393330	0.0000000
DolorPecho_TA	-1.3953657	0.5170118	-2.6989048	0.0069568
Glucemia_Sí	1.0399133	0.3051837	3.4074994	0.0006556
Electro_Normal	-0.4813833	0.3010275	-1.5991338	0.1097909
Electro_ST	-0.5114357	0.3832521	-1.3344630	0.1820522
AnginaEjercicio_S	0.7350136	0.2730957	2.6914144	0.0071150
PendienteST_Descendente	0.7830317	0.5133892	1.5252205	0.1272041
PendienteST_Plano	2.3945237	0.2767187	8.6532781	0.0000000

Usar el modelo de regresión logística ajustado para predecir el riesgo de infarto en el conjunto de test y mostrar las primeras 10 predicciones.

Solución

# Predecimos el riesgo de infarto en el conjunto de test utilizando el modelo de regresión logística ajustado.
modelo_entrenado |> predict(new_data = df_test) |> 
    head() |> 
    kable()

.pred_class
No
No
Sí
No
Sí
No

Añadir al conjunto de test la clase predicha con el modelo de regresión logística, así como las probabilidades de infarto predichas.

Ayuda

Usar la función augment del paquete parsnip para añadir al conjunto de test las probabilidades de infarto predichas por el modelo de regresión logística.

Parámetros:

new_data: el conjunto de datos de test.

Solución

# Añadimos al conjunto de test las probabilidades de infarto predichas por el modelo de regresión logística.
df_test <- modelo_entrenado |> augment(new_data = df_test)
df_test |> head() |> 
    kable()

.pred_class	.pred_No	.pred_Sí	Edad	Sexo	DolorPecho	PresionArterial	Colesterol	Glucemia	Electro	Pulsaciones	AnginaEjercicio	DepresionST	PendienteST	Infarto
No	0.9623340	0.0376660	40	H	ATA	140	289	No	Normal	172	N	0.0	Ascendente	No
No	0.9525000	0.0475000	37	H	ATA	130	283	No	ST	98	N	0.0	Ascendente	No
Sí	0.0629385	0.9370615	37	H	ASY	140	207	No	Normal	130	S	1.5	Plano	Sí
No	0.9880635	0.0119365	48	M	ATA	120	284	No	Normal	120	N	0.0	Ascendente	No
Sí	0.1544145	0.8455855	58	H	ATA	136	164	No	ST	99	S	2.0	Plano	Sí
No	0.9449769	0.0550231	39	H	ATA	120	204	No	Normal	145	N	0.0	Ascendente	No

Evaluar el rendimiento del modelo de regresión logística en el conjunto de test utilizando las siguientes métricas de clasificación: precisión, sensibilidad, especificidad, exactitud, recall y F1-score.
Ayuda
Utilizar la función metric_set del paquete yardstick para crear un conjunto de métricas de clasificación y pasarle el conjunto de datos de test aumentado con las probabilidades de infarto predichas.

Las métricas más habituales se calculan a partir de la matriz de confusión.

Predicción Positiva Predicción Negativa

Real Positivo VP (Verdaderos Positivos) FN (Falsos Negativos)

Real Negativo FP (Falsos Positivos) VN (Verdaderos Negativos)
- Exactitud (Accuracy): Proporción de predicciones correctas sobre el total de predicciones: (VP + VN) / (VP + VN + FP + FN). Es la métrica más básica.
- Precisión (Precision): Proporción de predicciones positivas correctas. Mide qué tan “preciso” es el modelo cuando predice positivo: VP / (VP + FP).
- Sensibilidad/Recall: Proporción de casos positivos reales que fueron correctamente clasificados por el modelo: VP / (VP + FN). También se llama “tasa de verdaderos positivos”.
- Especificidad: Proporción de casos negativos reales que fueron correctamente clasificados por el modelo: VN / (VN + FP). Es la “tasa de verdaderos negativos”.
- F1-score: Media armónica entre precisión y recall: 2 × (Precisión × Recall) / (Precisión + Recall). Es útil cuando quieres balancear tanto la precisión como el recall, especialmente con clases desbalanceadas.
Solución
# Creamos un conjunto de métricas de clasificación incluyendo exactitud, sensibilidad, especificidad, precisión y F1-score. metricas <- metric_set(accuracy, sensitivity, specificity, precision, f_meas) # Calculamos las métricas de clasificación en el conjunto de test. df_test |> metricas(truth = Infarto, estimate = .pred_class) |> kable()

.metric .estimator .estimate

accuracy binary 0.9021739

sensitivity binary 0.8536585

specificity binary 0.9411765

precision binary 0.9210526

f_meas binary 0.8860759
Dibujar la curva ROC del modelo de regresión logística y calcular el área bajo la curva (AUC).
Ayuda
Utilizar la función roc_curve del paquete yardstick para calcular la curva ROC y la función roc_auc para calcular el área bajo la curva (AUC).
Parámetros:
- truth: variable de verdad (real).
- .pred_No: probabilidad de la clase negativa.
Solución
# Dibujamos la curva ROC del modelo de regresión logística. df_test|> roc_curve(truth = Infarto, .pred_No) |> autoplot()

# Calculamos el área bajo la curva (AUC). df_test |> roc_auc(truth = Infarto, .pred_No) |> kable()

.metric .estimator .estimate

roc_auc binary 0.9414156

	Predicción Positiva	Predicción Negativa
Real Positivo	VP (Verdaderos Positivos)	FN (Falsos Negativos)
Real Negativo	FP (Falsos Positivos)	VN (Verdaderos Negativos)

.metric	.estimator	.estimate
accuracy	binary	0.9021739
sensitivity	binary	0.8536585
specificity	binary	0.9411765
precision	binary	0.9210526
f_meas	binary	0.8860759

.metric	.estimator	.estimate
roc_auc	binary	0.9414156

4.2 Ejercicios propuestos

Ejercicio 4.4 El conjunto de datos neonatos contiene información sobre una muestra de 320 recién nacidos en un hospital durante un año que cumplieron el tiempo normal de gestación.

Crear un data frame a con los datos de los neonatos a partir del fichero anterior.
Construir la recta de regresión del peso de los recién nacidos sobre el número de cigarros fumados al día por las madres. ¿Existe una relación lineal fuerte entre el peso y el número de cigarros?
Dibujar la recta de regresión calculada en el apartado anterior. ¿Por qué la recta no se ajusta bien a la nube de puntos?
Calcular y dibujar la recta de regresión del peso de los recién nacidos sobre el número de cigarros fumados al día por las madres en el grupo de las madres que si fumaron durante el embarazo. ¿Es este modelo mejor o pero que la recta del apartado anterior?
Según este modelo, ¿cuánto disminuirá el peso del recién nacido por cada cigarro más diario que fume la madre?
Según el modelo anterior, ¿qué peso tendrá un recién nacido de una madre que ha fumado 5 cigarros diarios durante el embarazo? ¿Y si la madre ha fumado 30 cigarros diarios durante el embarazo? ¿Son fiables estas predicciones?
¿Existe la misma relación lineal entre el peso de los recién nacidos y el número de cigarros fumados al día por las madres que fumaron durante el embarazo en el grupo de las madres menores de 20 y en el grupo de las madres mayores de 20? ¿Qué se puede concluir?

Ejercicio 4.5 El conjunto de datos glaucoma.csv contiene información sobre el grosor de los sectores de los anillos peripalilares de la capa de fibras nerviosas de la retina obtenidos mediante tomografía de coherencia óptica (OTC) en pacientes con y sin glaucoma. En la OTC se toman 4 anillos con distintos radios (BMO, 3.5 mm, 4.1 mm y 4.7 mm) y para cada anillo se miden 6 sectores (Nasal Superior, Nasal, Nasal Inferior, Temporal Inferior, Temporal y Temporal Superior) y también la media global. Los datos están ya normalizados.

Crear un data frame con los datos del fichero glaucoma.
Construir un modelo de regresión logística para predecir si un paciente tiene glaucoma o no a partir de los datos de la OTC. Utilizar la variable Glaucoma como variable dependiente y las variables de los anillos y sectores como variables independientes.
Evaluar el modelo de regresión logística calculando la matriz de confusión y las métricas de clasificación. Dibujar la curva ROC del modelo.