Cálculo integral Primitiva de una función Definición - Primitiva de una función. Se dice que la función $F(X)$ es una función primitiva de $f(x)$ si se verifica que $F’(x)=f(x)$ $\forall x \in \textrm{Dom}(f)$. Ejemplo. La función $F(x)=x^2$ es una primitiva de la función $f(x)=2x$ ya que $F’(x)=2x$ para todo $\mathbb{R}$. El cálculo de primitivas puede verse con un proceso inverso al cálculo de derivadas, y es por eso también se suele llamar antiderivada a la primitiva de una función. Integral indefinida de una función Si $F(x)$ es una función primitiva de $f(x)$ también lo será toda función de la forma $F(x)+C$, $\forall C \in \mathbb{R}$, de manera que si una función tiene primitiva, tiene infinitas primitivas que se obtienen añadiendo una constante a cualquiera de ellas. Definición - Integral indefinida. Se llama función integral indefinida de la función $f$ al conjunto de todas sus funciones primitivas y se representa como $$\int{f(x)}\,dx=F(x)+C$$ siendo $F(x)$ una función primitiva de $f(x)$ y $C$ una constante arbitraria. Ejemplo. La integral indefinida de $f(x)=2x$ es $$\int 2x\, dx = x^2+C.$$ Interpretación de la integral En temas anteriores se vio que la derivada de una función es la tasa de variación instantánea, de manera que si conocemos la tasa de variación instantánea de una función en cada instante, podemos averiguar la variación real de la función. Ejemplo. ¿Cuál sera el espacio recorrido por un objeto en caída libre? Cuando soltamos cualquier objeto desde una altura, la única fuerza que actúa sobre el es la gravedad, con una aceleración aproximada de $9.8$ m/s$^2$, esto quiere decir que la velocidad varía de forma constante y por tanto la velocidad del objeto en cada instante $t$ sera: $$v(t) = 9.8t \mbox{ m/s}.$$ Puesto que la velocidad en cada instante es la tasa de variación instantánea del espacio recorrido por el objeto, su primitiva nos dará el espacio recorrido por el objeto en cada instante: $$e(t) = \int 9.8t\, dt = 9,8\frac{t^2}{2}.$$ Así, por ejemplo, a los 2 segundos, el espacio recorrido será $e(2) = 9.8\frac{2^2}{2} = 19.6$ m. Linealidad de la integral Dadas dos funciones $f$ y $g$ que admiten primitiva, y una constante $k \in \mathbb{R}$ se verifica que $\int{(f(x)+g(x))}\,dx=\int{f(x)}\,dx+\int{g(x)}\,dx$, $\int{kf(x)}\,dx=k\int{f(x)}\,dx$. Integrales inmediatas $\int a\,dx=ax+C$, con $a$ constante. $\int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C$ si $n\neq -1$. $\int \dfrac{1}{x}\, dx=\ln\lvert x\rvert+C$. $\int e^x\,dx=e^x+C$. $\int a^x\,dx=\dfrac{a^x}{\ln a}+C$. $\int \operatorname{sen} x\, dx=-\cos x+C$. $\int \cos x\, dx=\operatorname{sen} x+C$. $\int \operatorname{tg} x\, dx=\ln\lvert\operatorname{sec} x\rvert+C$. $\int \operatorname{sec} x\, dx = \ln\lvert\operatorname{sec} x + \operatorname{tg} x\rvert+C$. $\int \operatorname{cosec} x\, dx= \ln\lvert\operatorname{cosec} x-\operatorname{cotg} x\rvert+C$. $\int \operatorname{cotg} x\, dx= \ln\lvert\operatorname{sen} x\rvert+C$. $\int \operatorname{sec}^2 x\, dx= \operatorname{tg} x+ C$. $\int \operatorname{cosec}^2 x\, dx= -\operatorname{cotg} x+ C$. $\int \operatorname{sec} x \operatorname{tg} x\, dx= \operatorname{sec} x+ C$. $\int \operatorname{cosec} x \operatorname{cotg} x\, dx = -\operatorname{cosec} x +C$. $\int \dfrac{dx}{\sqrt{a^2-x^2}}=\operatorname{arcsen}\dfrac{x}{a}+C$. $\int \dfrac{dx}{a^2+x^2}=\dfrac{1}{a}\operatorname{arctg}\dfrac{x}{a}+C$. $\int \dfrac{dx}{x\sqrt{x^2-a^2}}=\dfrac{1}{a}\operatorname{sec}^{-1}\dfrac{x}{a}+C$. $\int \dfrac{dx}{a^2-x^2}=\dfrac{1}{2a}\ln\lvert\dfrac{x+a}{x-a}\rvert+C$. Técnicas de integración Desgraciadamente, y a diferencia del cálculo de derivadas, no existe un procedimiento infalible que permita calcular la primitiva de una función siempre que exista. Existen no obstante, diferentes técnicas para integrar algunos tipos de funciones. Las técnicas más habituales son: Integración por partes Integración por reducción Integración por cambio de variable Integración de funciones racionales Integración de funciones trigonométricas Integración por partes Teorema - Integración por partes. Dadas $f$ y $g$, dos funciones derivables de $x$, $$\int{f’(x)g(x)}\,dx=f(x)g(x)-\int{g’(x)f(x)}\,dx,$$ o con notación diferencial, si $u$ y $v$ son funciones derivables de $x$ $$\int{u}\,dv=uv-\int{v}\,du.$$ Demostración De la regla de la derivada del producto se tiene $$ (uv)’ = u’v + uv’ $$ y calculando la integral a ambos lados se llega a $$ \begin{gathered} \int (uv)’ \, dx = \int u’v \, dx + \int uv’\, dx \Rightarrow\newline uv = \int v\,du + \int u\, dv \Rightarrow\newline \int{u}\,dv=uv-\int{v}\,du. \end{gathered} $$ Al emplear el método de integración por partes se debe realizar la elección de $u$ y $dv$ de tal forma que las integrales que haya que realizar sean lo más sencillas posibles. Ejemplo. Para integrar $\int{x \operatorname{sen} x}\,dx$ se deberá elegir $u=x$ y $dv=\operatorname{sen} x\, dx$, con lo que $du=dx$ y $v=-\cos x$, resultando $$\int{x \operatorname{sen} x}\,dx=-x\cos x-\int (-\cos x)\,dx = -x\cos x +\operatorname{sen} x.$$ Si hubiésemos elegido $u=\operatorname{sen} x$ y $dv=x\,dx$, la cosa se complica. Integración por reducción Las fórmulas de reducción permiten simplificar el cálculo cuando hay que aplicar la integración por partes varias veces consecutivas. Si se tiene que calcular una integral indefinida $I_n$ que depende de un número natural $n$, las fórmulas de reducción nos permitirán expresar $I_{n}$ en función de $I_{n-1}$, es decir se obtendrá una relación recurrente del tipo $$I_n=f(I_{n-1},x,n)$$ con lo que calculando una integral se pueden obtener fácilmente las demás. Ejemplo. Si se desea calcular $I_{n}=\int{x^{n}e^{x}}\,dx$, aplicando la integración por partes se debe elegir $u=x^{n}$ y $dv=e^{x}\,dx$, con lo que $du=nx^{n-1}\,dx$ y $v=e^{x}$, obteniéndose $$\ I_{n}=\int{x^{n}e^{x}}\,dx=x^{n}e^{x}-n\int{x^{n-1}e^{x}}\,dx=x^{n}e^{x}-nI_{n-1}.$$ Así, por ejemplo, para $n=3$ se tiene $$ \begin{aligned} \int x^3 e^x\, dx &= I_3 = x^3e^x-3I_2 = x^3e^x-3(x^2e^x-2I_1) = x^3e^x-3(x^2e^x-(xe^x-I_0) =\newline &= x^3e^x-3(x^2e^x-(xe^x-e^x) = e^x(x^3-3x^2+6x-6). \end{aligned} $$ Integración por cambio de variable La regla de la cadena establece que la derivada de una función compuesta $f(g(x))$ es $$f(g(x))’ = f’(g(x))g’(x),$$ de manera que es posible integrar esta última expresión haciendo un cambio de variable $u=g(x)$ de manera que $du=g’(x)dx$: $$\int f’(g(x))g’(x)\, dx = \int f’(u)\, du = f(u)+C = f(g(x))+C.$$ Ejemplo. Para calcular la integral $\int{\dfrac{1}{x\log x}}\, dx$ puede hacerse el cambio de variable $u=\log x$ con lo que $du=\frac{1}{x}dx$ y sustituyendo queda $$\int \frac{dx}{x\log x}=\int \frac{1}{\log x}\frac{1}{x}\,dx = \int \frac{1}{u}\,du = \log |u|+ C,$$ y deshaciendo el cambio tenemos $$\int \frac{1}{x\log x}\,dx= \log |\log x| + C.$$ Integración de funciones racionales Descomposición en fracciones simples Toda función racional se puede escribir como suma de un polinomio (que tiene primitiva inmediata) más una función racional propia, es decir, una función racional en la que el grado del numerador sea menor que el grado del denominador. A su vez, toda función racional propia puede expresarse como suma de fracciones simples de los tipos siguientes: $$\begin{array}{cl} \dfrac{A}{(x-a)}& \textrm{: con raíces reales simples del denominador.}\newline \dfrac{A}{(x-a)^{n}}& \textrm{: con raíces reales múltiples del denominador.}\newline \dfrac{Ax+B}{x^2+cx+d}& \textrm{: con raíces complejas simples del denominador.}\newline \dfrac{Ax+B}{(x^2+cx+d)^n} & \textrm{: con raíces complejas múltiples del denominador.} \end{array}$$ con $n>1$. Primitivas de fracciones simples Usando la linealidad de la integral, basta calcular la primitiva de cada una de estas fracciones simples para calcular la primitiva de la función racional: $$ \begin{aligned} \int \frac{A}{x-a}\,dx &= A\log|x-a|+C,\newline \int \frac{A}{(x-a)^n}\,dx &= \frac{-A}{(n-1)(x-a)^{n-1}}+C \textrm{ si $n\neq 1$}.\newline \int \frac{Ax+B}{x^2+cx+d} &= \frac{A}{2}\log|x^2+cx+d|+\frac{2B-Ac}{\sqrt{4d-c^2}}\operatorname{arctg} \frac{2x+c}{\sqrt{4d-c^2}}+C. \end{aligned} $$ Ejemplo - Raíces reales. Consideremos la función $f(x)=\dfrac{x^2+3x-5}{x^3-3x+2}$. Su denominador se puede factorizar como $x^3-3x+2=(x-1)^2(x+2)$ por lo que tiene una raíz simple -2 y una raíz múltiple 1. La descomposición en fracciones simples es: $$ \begin{aligned} \frac{x^2+3x-5}{x^3-3x+2}&=\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+2} = \newline &= \frac{A(x-1)(x+2)+ B(x+2)+C(x-1)^2}{(x-1)^2(x+2)} = \newline &= \frac{(A+C)x^2+(A+B-2C)x+(-2A+2B+C)}{(x-1)^2(x+2)} \end{aligned} $$ e igualando los numeradores tenemos $A=16/9$, $B=-1/3$ y $C=-7/9$, de modo que $$\frac{x^2+3x-5}{x^3-3x+2}= \frac{16/9}{x-1}+\frac{-1/3}{(x-1)^2}+\frac{-7/9}{x+2}.$$ Finalmente, integrando tenemos $$ \begin{aligned} \int \frac{x^2+3x-5}{x^3-3x+2}\, dx &= \int \frac{16/9}{x-1}\,dx+\int \frac{-1/3}{(x-1)^2}\,dx+\int \frac{-7/9}{x+2}\,dx = \newline &= \frac{16}{9}\int\frac{1}{x-1}\,dx-\frac{1}{3}\int(x-1)^{-2}\,dx- \frac{7}{9}\int \frac{1}{x+2}\,dx = \newline &= \frac{16}{9}\ln|x-1|+\frac{1}{3(x-1)}-\frac{7}{9}\ln|x+2|+C. \end{aligned} $$ Ejemplo - Raíces imaginarias. Consideremos la función $f(x)=\dfrac{x+1}{x^2-4x+8}$. En este caso el denominador no tiene raíces reales, pero puede escribirse de la forma $$x^2-4x+8 = (x-2)^2+4$$ Integrando, tenemos $$ \begin{aligned} \int \dfrac{x+1}{x^2-4x+8}\, dx &= \int \dfrac{x-2+3}{(x-2)^2+4}\,dx = \newline &= \int \dfrac{x-2}{(x-2)^2+4}\,dx + \int \dfrac{3}{(x-2)^2+4}\,dx = \newline &= \frac{1}{2}\ln|(x-2)^2+4| + \dfrac{3}{2}\operatorname{arctg}\left(\frac{x-2}{2}\right)+C. \end{aligned} $$ Integración de funciones trigonométricas Función $\sin^n x\cos^m x$ con $n$ o $m$ impares Si $f(x)=\sin^n x\cos^m x$ con $n$ o $m$ impares, entonces para integrar esta función se hace el cambio $\operatorname{sen} x = t$ o $\cos x =t$. Ejemplo. $$\int \operatorname{sen}^2 x\cos^3 x\, dx = \int \operatorname{sen}^2 x\cos^2 x\cos x\, dx = \int \operatorname{sen}^2 x(1-\operatorname{sen}^2 x)\cos x\, dx,$$ y haciendo el cambio $t=\operatorname{sen} x$, de modo que $dt = \cos x dx$, se tiene $$\int \operatorname{sen}^2 x(1-\operatorname{sen}^2 x)\cos x\, dx = \int t^2(1-t^2)\, dt = \int t^2-t^4\, dt = \frac{t^3}{3}-\frac{t^5}{5}+C,$$ y deshaciendo el cambio anterior se obtiene $$\int \operatorname{sen}^2 x\cos^3 x\, dx = \frac{\operatorname{sen}^3 x}{3}-\frac{\sin^5 x}{5}+C.$$ Función $\sin^n x\cos^m x$ con $n$ y $m$ pares Si $f(x)=\operatorname{sen}^n x\cos^m x$ con $n$ y $m$ pares, entonces se suelen utilizar las siguientes igualdades para facilitar el cálculo de la integral: $$ \begin{aligned} \operatorname{sen}^2 x &= \frac{1}{2}(1-\cos 2x)\newline \cos^2 x &= \frac{1}{2}(1+\cos 2x)\newline \operatorname{sen} x\cos x &= \frac{1}{2}\operatorname{sen} 2x \end{aligned} $$ Ejemplo. $$ \begin{aligned} \int \operatorname{sen}^2 x\cos^4 x\, dx &= \int (\operatorname{sen} x\cos x)^2\cos^2 x\, dx = \int \left(\frac{1}{2}\operatorname{sen} 2x\right)^2\frac{1}{2}(1+\cos 2x)\,dx =\newline &= \frac{1}{8}\int \operatorname{sen}^2 2x\,dx+\frac{1}{8}\int \sin^2 2x \cos 2x\,dx, \end{aligned} $$ siendo la primera integral es de este mismo tipo y la segunda del anterior $$\int \operatorname{sen}^2 x\cos^4 x\, dx = \frac{1}{32}x-\frac{1}{32}\operatorname{sen} 2x)+\frac{1}{24}\operatorname{sen}^3 2x.$$ Productos de senos y cosenos Las igualdades $$ \begin{aligned} \operatorname{sen} x\cos y &= \frac{1}{2}(\operatorname{sen}(x-y)+\operatorname{sen}(x+y))\newline \operatorname{sen} x\operatorname{sen} y &= \frac{1}{2}(\cos(x-y)-\cos(x+y))\newline \cos x\cos y &= \frac{1}{2}(\cos(x-y)+\cos(x+y)) \end{aligned} $$ transforman los productos en sumas, simplificando su integración. Ejemplo. $$ \begin{aligned} \int \operatorname{sen} x\cos 2x\, dx &= \int \frac{1}{2}(\operatorname{sen}(x-2x)+\operatorname{sen}(x+2x))\,dx = \newline &= \frac{1}{2}\int \operatorname{sen} (-x)\,dx +\frac{1}{2}\int \operatorname{sen} 3x\,dx = \newline &= \frac{1}{2}\cos(-x)- \frac{1}{6}\cos 3x +C. \end{aligned} $$ Funciones racionales de senos y cosenos Si $f(x,y)$ es una función racional entonces la función $f(\operatorname{sen} x,\cos x)$ puede convertirse en una función racional en $t$ mediante los cambios $$\operatorname{tg} \frac{x}{2}=t \quad \operatorname{sen} x=\frac{2t}{1+t^2} \quad \cos x = \frac{1-t^2}{1+t^2} \quad dx = \frac{2}{1+t^2}dt.$$ Ejemplo. $$\int \frac{1}{\operatorname{sen} x}\,dx = \int \frac{1}{\frac{2t}{1+t^2}}\frac{2}{1+t^2}\,dt = \int \frac{1}{t}\,dt = \log|t|+C = \log|\operatorname{tg}\frac{x}{2}|+C.$$ Integral definida Definición - Integral definida. Sea $f(x)$ una función continua en el intervalo $[a, b]$. 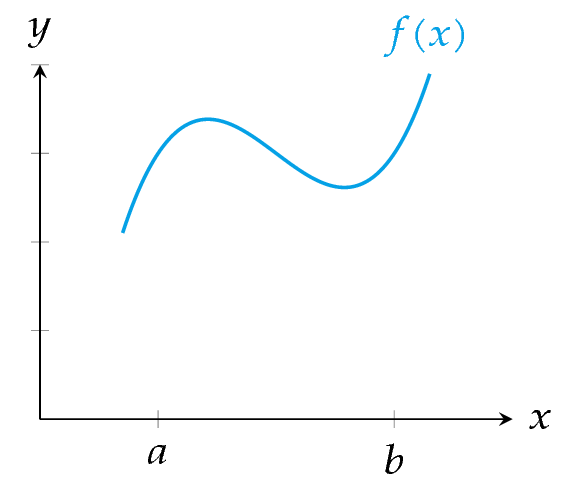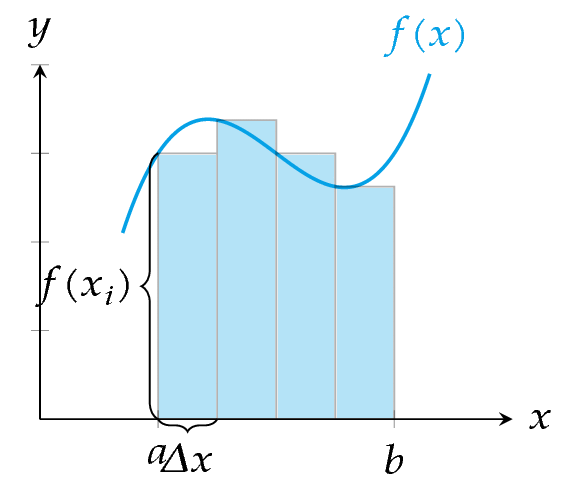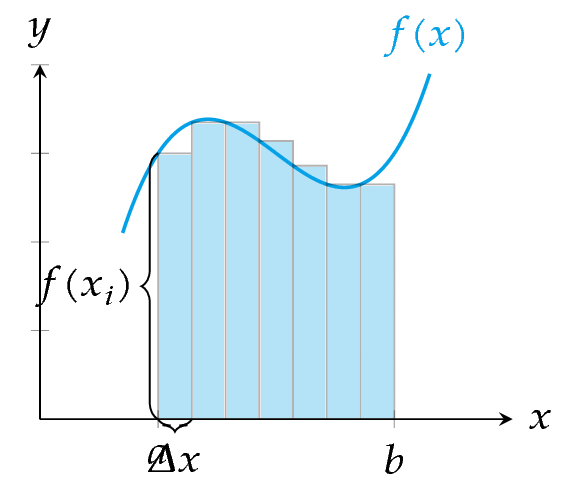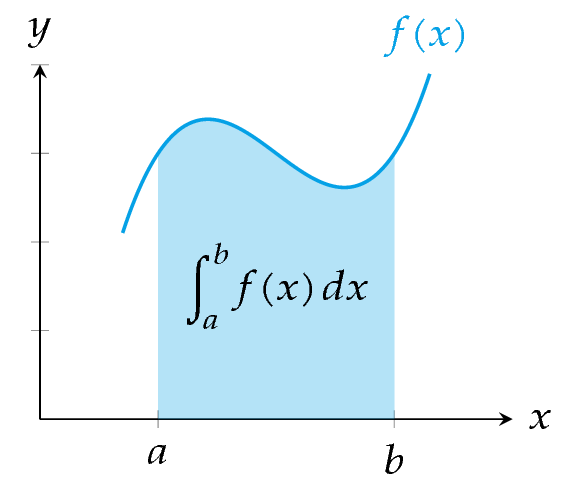Si se divide este intervalo en $n$ subintervalos de igual amplitud $\Delta x$ y se elige un punto cualquiera $x_i$ de cada subintervalo, la integral definida de $f$ desde $a$ hasta $b$ se define como el límite $$\int_a^b f(x)\,dx = \lim_{n\rightarrow \infty}\sum_{i=1}^n f(x_i)\Delta x.$$ Teorema - Primer teorema fundamental de Cálculo. Si $f(x)$ es una función continua en el intervalo $[a,b]$ y $F(x)$ es la primitiva de $f$ en $[a,b]$, entonces $$\int_a^b f(x)\,dx = F(b)-F(a)$$ Ejemplo. Dada la función $f(x)=x^2$, se tiene $$\int_1^2 x^2\,dx = \left[\frac{x^3}{3}\right]_1^2 = \frac{2^3}{3}-\frac{1^3}{3} = \frac{7}{3}.$$ Propiedades de la integral definida Dadas dos funciones $f$ y $g$ integrables en $[a,b]$ y $k \in \mathbb{R}$ se cumplen las siguientes propiedades $\int_a^b(f(x)+g(x))\,dx=\int_a^bf(x)\,dx+\int_a^bg(x)\,dx$ (linealidad) $\int_a^b{kf(x)}\,dx=k\int_a^b{f(x)}\,dx$ (linealidad) $\int_a^b{f(x)\,dx} \leq \int_a^b{g(x)\,dx}$ si $f(x)\leq g(x)\ \forall x \in [a,b]$ (monotonía) $\int_a^b{f(x)\,dx} = \int_a^c{f(x)\,dx}+\int_c^b{f(x)\,dx}$ para cualquier $c\in(a,b)$ (aditividad) $\int_a^b f(x)\,dx = -\int_b^a f(x)\,dx$ Cálculo de áreas Área delimitada por una función positiva y el eje de abscisas Si $f$ es una función integrable en un intervalo $[a,b]$ y $f(x)\geq 0\ \forall x\in[a,b]$, entonces la integral definida $$\int_a^b f(x)\,dx$$ mide le área que queda entre la el gráfico de la función $f$ y el eje de abscisas en el intervalo $[a,b]$. Área delimitada por una función negativa y el eje de abscisas Si $f$ es una función integrable en un intervalo $[a,b]$ y $f(x)\leq 0\ \forall x\in[a,b]$, entonces el área que queda entre el gráfico de la función $f$ y el eje de abscisas en el intervalo $[a,b]$ es $$-\int_a^b f(x)\,dx.$$ Área delimitada por una función y el eje de abscisas En general, si $f(x)$ es una función integrable en el intervalo $[a,b]$, no importa el signo de $f$ en $[a,b]$, el area entre el gráfico de la función $f$ y el eje de abscisas en el intervalo $[a,b]$ es $$\int_a^b \vert f(x)\vert\,dx.$$ Área delimitada por dos funciones Si $f$ y $g$ son dos funciones integrables en el intervalo $[a,b]$, entonces el área limitada por los gráficos de $f$ y $g$ en el intervalo $[a,b]$ es $$\int_{a}^{b}{\vert f(x)- g(x)\vert\,dx}.$$ Integral Primitiva Area Anterior Cálculo diferencial en una variable Siguiente Ecuaciones diferenciales ordinarias