Funciones vectoriales de una variable real

Los campos vectoriales más habituales se dan en plano real $\mathbb{R}^2$, donde se suelen representar así

$$f(t)=x(t)\mathbf{i}+y(t)\mathbf{j},$$

y en el espacio real $\mathbb{R}^3$, donde ser representan así

$$f(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k},$$

Representación gráfica de un campo vectorial

La representación gráfica de un campo vectorial en $\mathbb{R}^2$ es una trayectoria en el plano real.

La representación gráfica de un campo vectorial en $\mathbb{R}^3$ es una trayectoria en el espacio real.

Derivative of a vector field

The concept of derivative as the limit of the average rate of change of a function can be extended easily to vector fields.

Many properties of real functions of a single real variable can be extended to vector fields through its component functions. Thus, for instance, the derivative of a vector field can be computed from the derivatives of its component functions.

Kinematics: Curvilinear motion

The notion of derivative as a velocity along a trajectory in the real line can be generalized to a trajectory in any euclidean space $\mathbb{R}^n$.

In case of a two dimensional space $\mathbb{R}^2$, if $f(t)$ describes the position of a moving object in the real plane at any time $t$, taking as reference the coordinates origin $O$ and the unitary vectors ${\mathbf{i}=(1,0),\mathbf{j}=(0,1)}$, we can represent the position of the moving object $P$ at every moment $t$ with a vector $\vec{OP}=x(t)\mathbf{i}+y(t)\mathbf{j}$, where the coordinates

$$ \begin{cases} x=x(t)\newline y=y(t) \end{cases} \quad t\in \mbox{Dom}(f) $$

are the coordinate functions of $f$.

Example. Given the trajectory $f(t) = (\cos t,\sin t)$, $t\in \mathbb{R}$, whose image is the unit circumference centred in the coordinate origin, its coordinate functions are $x(t) = \cos t$, $y(t) = \sin t$, $t\in \mathbb{R}$, and its velocity is

$$\mathbf{v}=f’(t)=(x’(t),y’(t))=(-\sin t, \cos t).$$

In the moment $t=\pi/4$, the object is in position $f(\pi/4) = (\cos(\pi/4),\sin(\pi/4)) =(\sqrt{2}/2,\sqrt{2}/2)$ and it is moving with a velocity $\mathbf{v}=f’(\pi/4)=(-\sin(\pi/4),\cos(\pi/4))=(-\sqrt{2}/2,\sqrt{2}/2)$.

Observe that the module of the velocity vector is always 1 as $\vert\mathbf{v}\vert=\sqrt{(-\sin t)^2+(\cos t)^2}=1$.

Tangent line to a trajectory

Tangent line to a trajectory in the plane

Vectorial equation

Given a trajectory $f(t)$ in the real plane, the vectors that are parallel to the velocity $\mathbf{v}$ at a moment $a$ are called tangent vectors to the trajectory $f$ at the moment $a$, and the line passing through $P=f(a)$ directed by $\mathbf{v}$ is the tangent line to the graph of $f$ at the moment $a$.

Example. We have seen that for the trajectory $f(t) = (\cos t,\sin t)$, $t\in \mathbb{R}$, whose image is the unit circumference centred at the coordinate origin, the object position at the moment $t=\pi/4$ is $f(\pi/4)=(\sqrt{2}/2,\sqrt{2}/2)$ and its velocity $\mathbf{v}=(-\sqrt{2}/2,\sqrt{2}/2)$. Thus the equation of the tangent line to $f$ at that moment is

$$ \begin{aligned} l: (x,y) & = f(\pi/4)+t\mathbf{v} = \left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)+t\left(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right) =\newline & =\left(\frac{\sqrt{2}}{2}-t\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2}\right). \end{aligned} $$

Cartesian and point-slope equations

From the vectorial equation of the tangent to a trajectory $f(t)$ at the moment $t=a$ we can get the coordinate functions

$$ \begin{cases} x=x(a)+tx’(a)\newline y=y(a)+ty’(a) \end{cases} \quad t\in \mathbb{R}, $$

and solving for $t$ and equalling both equations we get the Cartesian equation of the tangent

$$\frac{x-x(a)}{x’(a)}=\frac{y-y(a)}{y’(a)},$$

if $x’(a)\neq 0$ and $y’(a)\neq 0$.

From this equation it is easy to get the point-slope equation of the tangent

$$y-y(a)=\frac{y’(a)}{x’(a)}(x-x(a)).$$

Example. Using the vectorial equation of the tangent of the previous example

$$l: (x,y)=\left(\frac{\sqrt{2}}{2}-t\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2}\right),$$

its Cartesian equation is $$\frac{x-\sqrt{2}/2}{-\sqrt{2}/2} = \frac{y-\sqrt{2}/2}{\sqrt{2}/2}$$ and the point-slope equation is

$$y-\sqrt{2}/2 = \frac{-\sqrt{2}/2}{\sqrt{2}/2}(x-\sqrt{2}/2) \Rightarrow y=-x+\sqrt{2}.$$

Normal line to a trajectory in the plane

We have seen that the tangent line to a trajectory $f(t)$ at $a$ is the line passing through the point $P=f(a)$ directed by the velocity vector $\mathbf{v}=f’(a)=(x’(a),y’(a))$. If we take as direction vector a vector orthogonal to $\mathbf{v}$, we get another line that is known as normal line to the trajectory.

The Cartesian equation is

$$\frac{x-x(a)}{y’(a)} = \frac{y-y(a)}{-x’(a)},$$

and the point-slope equation is

$$y-y(a) = \frac{-x’(a)}{y’(a)}(x-x(a)).$$

Example. Considering again the trajectory of the unit circumference $f(t) = (\cos t,\sin t)$, $t\in \mathbb{R}$, the normal line to the graph of $f$ at moment $t=\pi/4$ is

$$ \begin{aligned} l: (x,y)&=(\cos(\pi/2),\sin(\pi/2))+t(\cos(\pi/2),\sin(\pi/2)) =\newline &= \left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)+t\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right) =\left(\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}+t\frac{\sqrt{2}}{2}\right), \end{aligned} $$

the Cartesian equation is

$$\frac{x-\sqrt{2}/2}{\sqrt{2}/2} = \frac{y-\sqrt{2}/2}{\sqrt{2}/2},$$ and the point-slope equation is $$y-\sqrt{2}/2 = \frac{\sqrt{2}/2}{\sqrt{2}/2}(x-\sqrt{2}/2) \Rightarrow y=x.$$

Tangent and normal lines to a function

A particular case of tangent and normal lines to a trajectory are the tangent and normal lines to a function of one real variable. For every function $y=f(x)$, the trajectory that trace its graph is

$$g(x) = (x,f(x)) \quad x\in \mathbb{R},$$

and its velocity is

$$g’(x) = (1,f’(x)),$$

so that the tangent line to $g$ at the moment $a$ is

$$\frac{x-a}{1} = \frac{y-f(a)}{f’(a)} \Rightarrow y-f(a) = f’(a)(x-a),$$

and the normal line is

$$\frac{x-a}{f’(a)} = \frac{y-f(a)}{-1} \Rightarrow y-f(a) = \frac{-1}{f’(a)}(x-a).$$

Example. Given the function $y=x^2$, the trajectory that traces its graph is $g(x)=(x,x^2)$ and its velocity is $g’(x)=(1,2x)$. At the moment $x=1$ the trajectory passes through the point $(1,1)$ with a velocity $(1,2)$. Thus, the tangent line at that moment is

$$\frac{x-1}{1} = \frac{y-1}{2} \Rightarrow y-1 = 2(x-1) \Rightarrow y = 2x-1,$$

and the normal line is

$$\frac{x-1}{2} = \frac{y-1}{-1} \Rightarrow y-1 = \frac{-1}{2}(x-1) \Rightarrow y = \frac{-x}{2}+\frac{3}{2}.$$

Tangent line to a trajectory in the space

The concept of tangent line to a trajectory can be easily extended from the real plane to the three-dimensional space $\mathbb{R}^3$.

If $f(t)=(x(t),y(t),z(t))$, $t\in \mathbb{R}$, is a trajectory in the real space $\mathbb{R}^3$, then at the moment $a$, the moving object that follows this trajectory will be at the position $P=(x(a),y(a),z(a))$ with a velocity $\mathbf{v}=f’(t)=(x’(t),y’(t),z’(t))$. Thus, the tangent line to $f$ at this moment have the following vectorial equation

$$ \begin{aligned} l&: (x,y,z)=(x(a),y(a),z(a))+t(x’(a),y’(a),z’(a)) =\newline &= (x(a)+tx’(a),y(a)+ty’(a),z(a)+tz’(a)), \end{aligned} $$

and the Cartesian equations are $$\frac{x-x(a)}{x’(a)}=\frac{y-y(a)}{y’(a)}=\frac{z-z(a)}{z’(a)},$$ provided that $x’(a)\neq 0$, $y’(a)\neq 0$ y $z’(a)\neq 0$.

Example. Given the trajectory $f(t)=(\cos t, \sin t, t)$, $t\in \mathbb{R}$ in the real space, at the moment $t=\pi/2$ the trajectory passes through the point

$$f(\pi/2)=(\cos(\pi/2),\sin(\pi/2),\pi/2)=(0,1,\pi/2),$$

with velocity

$$\mathbf{v}=f’(\pi/2)=(-\sin(\pi/2),\cos(\pi/2), 1)=(-1,0,1),$$

and the tangent line to the graph of $f$ at that moment is

$$l:(x,y,z)=(0,1,\pi/2)+t(-1,0,1) = (-t,1,t+\pi/2).$$

Interactive Example

Normal plane to a trajectory in the space

In the three-dimensional space $\mathbb{R}^3$, the normal line to a trajectory is not unique. There are an infinite number of normal lines and all of them are in the normal plane.

If $f(t)=(x(t),y(t),z(t))$, $t\in \mathbb{R}$, is a trajectory in the real space $\mathbb{R}^3$, then at the moment $a$, the moving object that follows this trajectory will be at the position $P=(x(a),y(a),z(a))$ with a velocity $\mathbf{v}=f’(t)=(x’(t),y’(t),z’(t))$. Thus, using the velocity vector as normal vector the normal plane to $f$ at this moment have the following vectorial equation

$$ \begin{aligned} \Pi &: (x-x(a),y-y(a),z-z(a))(x’(a),y’(a),z’(a)) = 0\newline &= x’(a)(x-x(a))+y’(a)(y-y(a))+z’(a)(z-z(a))=0. \end{aligned} $$

Example. For the trajectory of the previous example $f(t)=(\cos t, \sin t, t)$, $t\in \mathbb{R}$, at the moment $t=\pi/2$ the trajectory passes through the point

$$f(\pi/2)=(\cos(\pi/2),\sin(\pi/2),\pi/2)=(0,1,\pi/2),$$

with velocity

$$\mathbf{v}=f’(\pi/2)=(-\sin(\pi/2),\cos(\pi/2), 1)=(-1,0,1),$$ and normal plane to the graph of $f$ at that moment is

$$\Pi:\left(x-0,y-1,z-\frac{\pi}{2}\right)(-1,0,1) =0 \Leftrightarrow -x+z-\frac{\pi}{2}=0.$$

Interactive Example

Funciones de varias variables

En numerosos problemas de geometría, física y ciencias naturales nos encontramos a menudo con variables o factores que dependen o están relacionados con otros dos, tres o más factores:

• El área de un triángulo depende de dos factores que son su base y su altura.
• El volumen que ocupa un gas perfecto depende de dos factores que son su presión y su temperatura.
• El camino recorrido por un cuerpo en un movimiento de caída libre depende de multitud de factores entre los que cabe destacar: el tiempo que dure la caída, el área de la sección transversal del cuerpo, la latitud del lugar, la altura sobre el nivel del mar, la presión del aire, la temperatura del aire, etc.

Estas dependencias se expresan con funciones de varias variables.

Ejemplos.

• El área de un triángulo es la función real de dos variables reales

$$f(x,y)=\frac{xy}{2}.$$

• El volumen de un gas perfecto es otra función real de dos variables

  $$v=f(t,p)=\frac{nRt}{p},$$

  con $n$ y $R$ constantes.

Gráfica de una función de dos variables

La representación gráfica cartesiana de una función de dos variables $f(x,y)$ es una superficie del espacio real $\mathbb{R}^3$ donde cada punto de la superficie tiene coordenadas $(x,y,z)$, siendo $z=f(x,y)$.

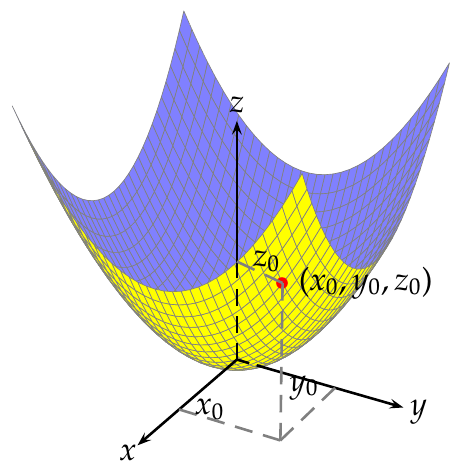
Ejemplos. La función $f(x,y)=\dfrac{xy}{2}$ que mide el área de un triángulo de base $x$ y altura $y$ tiene la siguiente representación gráfica:

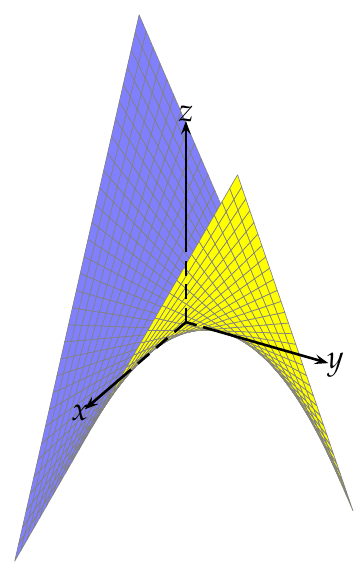
Y la función $\displaystyle f(x,y)=\frac{\operatorname{sen}(x^2+y^2)}{\sqrt{x^2+y^2}}$ tiene la siguiente representación gráfica tan peculiar:

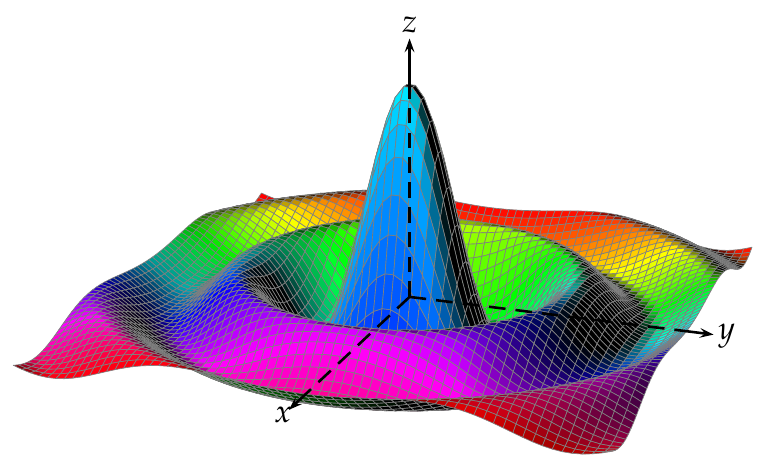
Conjunto de nivel de un campo escalar

Ejemplo. Si $f(x,y)=x^2+y^2$ y $P=(1,1)$, el conjunto de nivel de $f$ que incluye al punto $P$ es

$$C_{f,2} = {(x,y): f(x,y)=f(1,1)=2} = {(x,y): x^2+y^2=2},$$

que es la circunferencia del plano real centrada en el origen y de radio $\sqrt{2}$.

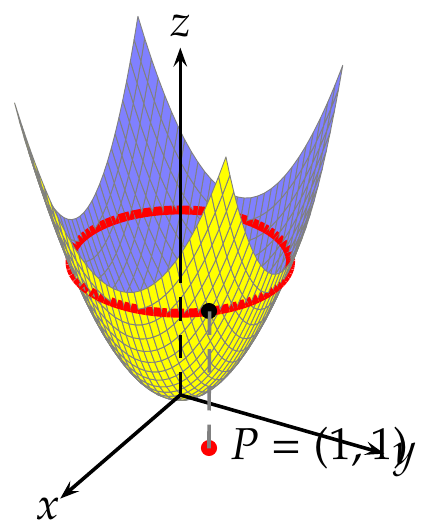
Funciones parciales

Ejemplo. Si consideramos la función del área de un triángulo

$$f(x,y)=\frac{xy}{2},$$

y fijamos el valor de la base $x=c$, entonces el área del triángulo ya sólo depende de la altura y $f$ se convierte en una función de una sola variable, que es la función parcial:

$$f_1(y)=f(c,y)=\frac{cy}{2},$$

con $c$ constante.

Noción de derivada parcial

Variación de una función con respecto a una variable

Al igual que medíamos la variación de una función de una variable, tiene sentido medir la variación de una función de varias variables con respecto a cada una de sus variables.

Sea $z=f(x,y)$ un campo escalar de $\mathbb{R}^2$. Si estamos en el punto $(x_0,y_0)$ y nos movemos una cantidad $\Delta x$ en la dirección del eje $X$, entonces, al mantenerse la coordenada $y$ constante, pasaremos desde el punto $(x_0,y_0)$ al punto $(x_0+\Delta x,y_0)$, y la variación que experimenta la función será

$$\Delta z=f(x_0+\Delta x,y_0)-f (x_0,y_0).$$

La variación relativa que experimenta la función con respecto a la variable $x$ vendrá dada por el cociente

$$\frac{\Delta z}{\Delta x}=\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}.$$

Tasa de variación instantánea de un campo escalar con respecto a una variable

Si en lugar de medir la variación de una función con respecto a una variable en un intervalo, medimos la variación en un punto, es decir, cuando $\Delta x$ tiende a 0, entonces obtenemos una tasa de variación instantánea:

$$\lim_{\Delta x\rightarrow 0}\frac{\Delta z}{\Delta x}=\lim_{\Delta x \rightarrow 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}.$$

Al valor del límite, cuando existe, también se le conoce como derivada parcial de $f$ con respecto a la variable $x$ en el punto $(x_0,y_0)$ y se nota

$$\frac{\partial f}{\partial x}(x_0,y_0).$$

Esta derivada parcial mide la tasa de variación instantánea de $f$ en el punto $P=(x_0,y_0)$ cuando $P$ se mueve en la dirección del eje $X$.

Interpretación geométrica de la derivada parcial

Geométricamente, $z=f(x,y)$ define una superficie. Si se corta esta superficie con el plano de ecuación $y=y_0$ (es decir, si $y$ se fija como una constante), la intersección de este plano con la superficie es una curva plana cuya pendiente en el punto $(x_0,y_0)$ es la derivada parcial de $f$ con respecto a $x$ en el punto $(x_0,y_0)$.

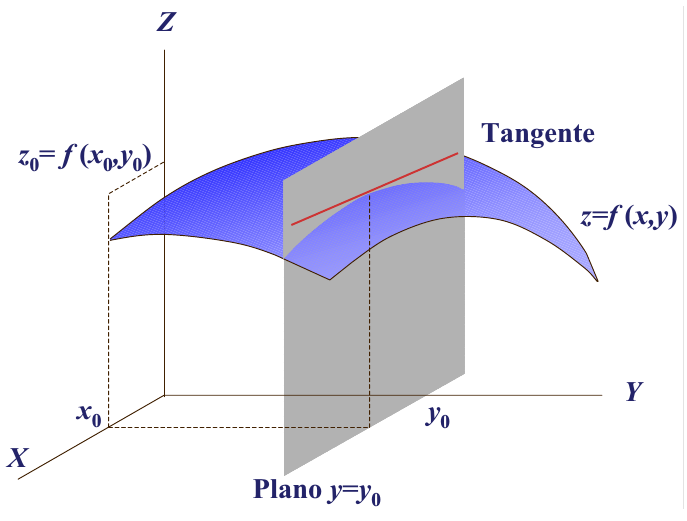
Derivada parcial

El concepto de derivada parcial visto para funciones de dos variables puede extenderse fácilmente para funciones de $n$ variables.

La definición de derivada para funciones de una variable es un caso particular de esta definición para $n=1$.

Cálculo de la derivada parcial

Al medir la variación de $f$ con respecto a la variación de una sola de sus variables $x_i$ en un punto $a=(a_1,\ldots,a_n)$, el resto de las variables se pueden considerar como constantes y, en tal caso, podemos ver a $f$ como una función parcial $i$-ésima

$$f_i(x_i)=f(a_1,\ldots,a_{i-1},x_i,a_{i+1},\ldots,a_n).$$

La derivada parcial de $f$ con respecto a $x_i$ puede calcularse derivando esta función:

$$\frac{\partial f}{\partial x_i}(a)=f_i’(a_i).$$

Regla. Para derivar parcialmente $f(x_1,\ldots,x_n)$ con respecto a una variable $x_i$, se deriva $f$ como si la única variable fuese $x_i$, tratando el resto de las variables como constantes.

Ejemplo En la ecuación de estado de los gases perfectos, el volumen es una función que depende de dos variables

$$v(t,p)=\frac{nRt}{p},$$

donde $t$ mide la temperatura, $p$ la presión y $n$ y $R$ son constantes.

La tasa de variación instantánea que experimenta el volumen con respecto a la presión viene dada por la derivada parcial de $v$ con respecto a $p$.

Para calcular esta derivada parcial se fija $t$ como constante y se deriva $v$ como si la única variable fuese $p$:

$$\frac{\partial v}{\partial p}(t,p)=\frac{d}{dp}\left(\frac{nRt}{p}\right)_{\mbox{$t=$cte}}=\frac{-nRt}{p^2}.$$

Del mismo modo, la tasa de variación instantánea del volumen conrespecto a la temperatura es:

$$\frac{\partial v}{\partial t}(t,p)=\frac{d}{dt}\left(\frac{nRt}{p}\right)_{\mbox{$p=$cte}}=\frac{nR}{p}.$$

Vector gradiente

Más adelante se mostrará que vector gradiente en un punto dado tiene la misma magnitud y dirección que la velocidad máxima de variación de la función en ese punto.

De este modo, , mientras que $-\nabla f(a)$ indica la dirección de máximo decrecimiento.

Ejemplo. Al calentar una superficie la temperatura $t$ (en ºC) en cada punto $(x,y,z)$ (en m) de dicha superficie viene dada por la función:

$$t(x,y,z)=\frac{x}{y}+z^2.$$

La dirección en la que más rápidamente aumenta la temperatura nos la da el vector gradiente

$$\nabla t(x,y,z)=\left(\frac{\partial t}{\partial x}(x,y,z),\frac{\partial t}{\partial y}(x,y,z),\frac{\partial t}{\partial z}(x,y,z)\right)=\left(\frac{1}{y},\frac{-x}{y^2},2z\right).$$

Si estamos, por ejemplo, en el punto $(2,1,1)$ dicha dirección será

$$\nabla t(2,1,1)=\left(\frac{1}{1},\frac{-2}{1^2},2\cdot 1\right)=(1,-2,2),$$

y su magnitud

$$|\nabla f(2,1,1)|=|\sqrt{1^2+(-2)^2+2^2}|=|\sqrt{9}|=3 \mbox{ $^\circ$C/m}.$$

Composición de una trayectoria con un campo escalar

Regla de la cadena

Si $f:\mathbb{R}^n\rightarrow \mathbb{R}$ es un campo escalar y $g:\mathbb{R}\rightarrow \mathbb{R}^n$ es una trayectoría, entonces es posible componer $g$ con $f$, de manera que $f\circ g:\mathbb{R}\rightarrow \mathbb{R}$ es una función real de variable real.

Teorema - Regla de la cadena. Si $f:\mathbb{R}^n\rightarrow \mathbb{R}$ es un campo escalar y $g:\mathbb{R}\rightarrow \mathbb{R}^n$ es una trayectoría, entonces

$$(f\circ g)’(t) = \nabla f(g(t))\cdot g’(t).$$

Ejemplo. Si se toma el campo escalar del plano real $f(x,y)=x^2y$ y la trayectoria $g(t)=(\cos t,\operatorname{sen} t)$ $t\in [0,2\pi]$ del mismo plano, entonces

$$\nabla f(x,y) = (2xy, x^2) \quad \mbox{y} \quad g’(t) = (-\operatorname{sen} t, \cos t),$$

y

$$(f\circ g)’(t) = \nabla f(g(t))\cdot g’(t) = (2\cos t\operatorname{sen} t,\cos^2 t)\cdot (-\operatorname{sen} t,\cos t) = -2\cos t\operatorname{sen}^2 t+\cos^3 t.$$

Se puede llegar al mismo resultado, sin aplicar la regla de la cadena, derivando directamente la función compuesta

$$(f\circ g)(t) = f(g(t)) = f(\cos t, \operatorname{sen} t) = \cos^2 t\operatorname{sen} t,$$

de manera que

$$(f\circ g)’(t) = 2\cos t(-\operatorname{sen} t)\operatorname{sen} t+\cos^2 t \cos t = -2\cos t\operatorname{sen}^2 t+\cos^3 t.$$

La regla de la cadena para la composición de un campo escalar con una trayectoria permite obtener fácilmente el álgebra de derivadas para funciones reales de una variable real:

$$ \begin{aligned} (u+v)’ &= u’+v’\newline (uv)’ &= u’v+uv’\newline \left(\frac{u}{v}\right)’ &= \frac{u’v-uv’}{v^2}\newline (u\circ v)’ &= u’(v)v' \end{aligned} $$

Para deducir la derivada de la suma se toma el campo escalar $f(x,y)=x+y$ y la trayectoria $g(t)=(u(t),v(t))$, de manera que aplicando la regla de la cadena se tiene

$$(u+v)’(t) = (f\circ g)’(t) = \nabla f(g(t))\cdot g’(t) = (1,1)\cdot (u’(t),v’(t)) = u’(t)+v’(t).$$

y para deducir derivada del producto, tomando $f(x,y)=xy$, se tiene

$$(uv)’(t) = (f\circ g)’(t) = \nabla f(g(t))\cdot g’(t) = (v(t),u(t))\cdot (u’(t),v’(t)) = u’(t)v(t)+u(t)v’(t).$$

Derivada direccional

Para un campo escalar $f(x,y)$ de $\mathbb{R}^2$ y un punto $P=(x_0,y_0)$, se vió que $\dfrac{\partial f}{\partial x}$ es la tasa de variación instantánea de $f$ con respecto a $x$ en el punto $P$, es decir, cuando nos desplazamos desde el punto $P$ en la dirección del eje $X$.

Del mismo modo, $\dfrac{\partial f}{\partial y}$ es la tasa de variación instantánea de $f$ con respecto a $y$ en el punto $P$, es decir, cuando nos desplazamos desde el punto $P$ en la dirección del eje $Y$.

Pero, ¿qué pasa si nos movemos en cualquier otra dirección?

La tasa de variación instantánea de $f$ en un punto $P$ en la dirección de un vector unitario cualquiera $u$ se conoce como derivada direccional.

Si se considera un vector unitario $\mathbf{u}$, la trayectoria que pasa por $P$, dirigida por $\mathbf{u}$, tiene ecuación

$$g(t)=P+t\mathbf{u},\ t\in\mathbb{R},$$ que para $t=0$, pasa por $P=g(0)$ con velocidad $\mathbf{u}=g’(0)$.

Así, la tasa de variación de $f$ a partir del punto $P$ en la dirección de $\mathbf{u}$ es

$$(f\circ g)’(0) = \nabla f(g(0))\cdot g’(0) = \nabla f(P)\cdot \mathbf{u}.$$

Obsérvese que las derivadas parciales son las derivadas direccionales en las direcciones de los vectores coordenados.

Ejemplo. Dada la función $f(x,y) = x^2+y^2$, su vector gradiente es

$$\nabla f(x,y) = (2x,2y),$$

de manera que la derivada direccional en el punto $P=(1,1)$, en la dirección del vector unitario $\mathbf{u}=(1/\sqrt{2},1/\sqrt{2})$ es

$$f’_{\mathbf{u}}(P) = \nabla f(P)\cdot \mathbf{u} = (2,2)\cdot(1/\sqrt{2},1/\sqrt{2}) = \frac{2}{\sqrt{2}}+\frac{2}{\sqrt{2}} = \frac{4}{\sqrt{2}}.$$

Para calcular la derivada direccional en la dirección de un vector no unitario $\mathbf{v}$, basta con convertirlo en unitario mediante la transformación

$$\mathbf{v’}=\frac{\mathbf{v}}{|\mathbf{v}|}.$$

Crecimiento de un campo escalar a partir del gradiente

Como se ha visto, para un vector unitario $\mathbf{u}$

$$f’_{\mathbf{u}}(P) = \nabla f(P)\cdot \mathbf{u} = |\nabla f(P)|\cos \theta,$$

donde $\theta$ es el ángulo que forma $\mathbf{u}$ con el vector gradiente $\nabla f(P)$.

Teniendo en cuenta que $-1\leq \cos\theta\leq 1$, para cualquier vector $\mathbf{u}$ se cumple

$$-|\nabla f(P)|\leq f’_{\mathbf{u}}(P)\leq |\nabla f(P)|.$$

Además, si $\mathbf{u}$ tiene la misma dirección y sentido que el gradiente, se tiene

$$f’_{\mathbf{u}}(P)=\lvert \nabla f(P)\rvert \cos 0=\lvert \nabla f(P)\rvert .$$

Por tanto, el crecimiento máximo de un campo escalar se produce en la dirección y sentido del gradiente.

Del mismo modo, si $\mathbf{u}$ tiene la misma dirección y sentido opuesto al gradiente, se tiene

$$f’_{\mathbf{u}}(P)=\lvert \nabla f(P)\rvert \cos \pi=-\lvert \nabla f(P)\rvert.$$

Por tanto, el decrecimiento máximo de un campo escalar se produce en la dirección y sentido opuesto al gradiente.

Derivación implícita

Si se sabe que la ecuación $$f(x,y)=0$$ define a $y$ como función de $x$, $y=h(x)$, alrededor de cierto valor $x=x_0$ para el que $y=h(x_0)=y_0$, entonces, si se toma la trayectoria $g(x)=(x,h(x))$, la ecuación anterior se puede expresar como

$$(f\circ g)(x) = f(g(x)) = f(x,h(x))=0,$$

de modo que usando la regla de la cadena sobre se tiene

$$(f\circ g)’(x) = \nabla f(g(x))\cdot g’(x) = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\cdot (1,h’(x)) = \frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}h’(x) = 0,$$

de donde se deduce

$$y’=h’(x)=\frac{-\dfrac{\partial f}{\partial x}}{\dfrac{\partial f}{\partial y}}$$

A este proceso que permite obtener $y’$ en un entorno de $x_0$ sin disponer de la fórmula explícita $y=h(x)$, se le llama derivación implícita.

Ejemplo. La ecuación $x^2+y^2=1$ define a la circunferencia de radio 1 centrada en el origen de coordenadas, que también puede expresarse como

$$f(x,y) = x^2+y^2-1 = 0.$$

Si se piensa en $y$ como función implícita de $x$, se tiene

$$y’=\frac{-\dfrac{\partial f}{\partial x}}{\dfrac{\partial f}{\partial y}} = \frac{-2x}{2y}=\frac{-x}{y}.$$

Podría llegarse al mismo resultado, despejando $y$ de la ecuación de la circunferencia,

$$x^2+y^2=1 \Leftrightarrow y^2=1-x^2 \Leftrightarrow y= \pm\sqrt{1-x^2}.$$

Si se toma la raíz positiva, que corresponde a la semicircunferencia superior, la derivada vale

$$y’ = \frac{1}{2\sqrt{1-x^2}}(-2x) = \frac{-x}{\sqrt{1-x^2}},$$

que coincide con el resultado de la derivación implícita, teniendo en cuenta que $y=\sqrt{1-x^2}$.

Propiedad del gradiente

Teorema. Sea $C$ el conjunto de nivel de un campo escalar $f$ que incluye a un punto $P$. Si $\mathbf{v}$ es la velocidad al pasar por $P$ de una trayectoria que circule por $C$, entonces

$$\nabla f(P) \cdot \mathbf{v} = 0.$$

Es decir, el vector gradiente de $f$ en $P$ es normal a $C$ en $P$, siempre que no sea nulo.

Demostración. Si se considera una trayectoria $g(t)$ a lo largo del conjunto de nivel $C$ que pase por $P=g(t_0)$, de modo que $\mathbf{v}=g’(t_0)$, entonces

$$(f\circ g)(t) = f(g(t)) = f(P),$$

que es constante para cualquier $t$, y al aplicar la regla de la cadena se tiene

$$(f\circ g)’(t) = \nabla f(g(t))\cdot g’(t) = 0,$$

de modo que, cuanto $t=t_0$, se tiene

$$\nabla f(P)\cdot \mathbf{v} = 0.$$

Rectas normal y tangente a una linea en el plano

Según el resultado anterior, la recta normal a una línea $f(x,y)=0$ en un punto $P=(x_0,y_0)$, tiene ecuación

$$P+t\nabla f(P) = (x_0,y_0)+t\nabla f(x_0,y_0).$$

Ejemplo. Dado el campo escalar $f(x,y)=x^2+y^2-1$, y el punto $P=(0,1)$, resulta que el conjunto de nivel que pasa por $P$, para el que $f(x,y)=f(P)=0$ es la circunferencia de radio 1 centrada en el origen. Así pues, tomando como vector normal el gradiente de $f$ $$\nabla f(x,y) = (2x,2y),$$ que en el punto $P=(0,1)$ vale $\nabla f(0,1) = (0,2)$, la recta normal a la circunferencia en $P$ es

$$P+t\nabla f(P) = (0,1)+t(0,2) = (0,1+2t),$$

que se trata de la recta vertical $x=0$, que coincide con el eje $Y$.

y la recta tangente a la circunferencia en $P$ es

$$((x,y)-P)\cdot \nabla f(P) = ((x,y)-(0,1))\cdot (0,2) = (x,y-1)\cdot(0,2) = 2(y-1) = 0 \Rightarrow y=1.$$

Recta normal y plano tangente a una superficie

De mismo modo, si en lugar de una línea en el plano se tiene una superficie $f(x,y,z)=0$, en el punto $P=(x_0,y_0,z_0)$ la recta normal tiene ecuación

$$P+t\nabla f(P) = (x_0,y_0,z_0)+t\nabla f(x_0,y_0,z_0).$$

Dada el campo escalar $f(x,y,z)=x^2+y^2-z$, y el punto $P=(1,1,2)$, resulta que el conjunto de nivel que pasa por $P$, para el que $f(x,y)=f(P)=0$, es el paraboloide $z=x^2+y^2$. Así pues, tomando como vector normal el gradiente de $f$, que vale

$$\nabla f(x,y,z) = (2x,2y,-1),$$

que en el punto $P=(1,1,2)$ vale $\nabla f(1,1,2) = (2,2,-1)$, la recta normal al paraboloide en $P$ es

$$P+t\nabla f(P) = (1,1,2)+t\nabla f(1,1,2) = (1,1,2)+t(2,2,-1) = (1+2t,1+2t,2-t),$$

que se trata de la recta de ecuaciones $x=y$ y $x=5-2z$.

Y el plano tangente al paraboloide en $P$ es

$$ \begin{aligned} ((x,y,z)-P)\cdot \nabla f(P) &= ((x,y,z)-(1,1,2))(2,2,-1) = (x-1,y-1,z-2)(2,2,-1)=\newline &= 2(x-1)+2(y-1)-(z-2) = 2x+2y-z-2= 0. \end{aligned} $$

Ejemplo. La gráfica del paraboloide $f(x,y,z)=x^2+y^2-z=0$ y su plano tangente en el punto $P=(1,1,2)$ es

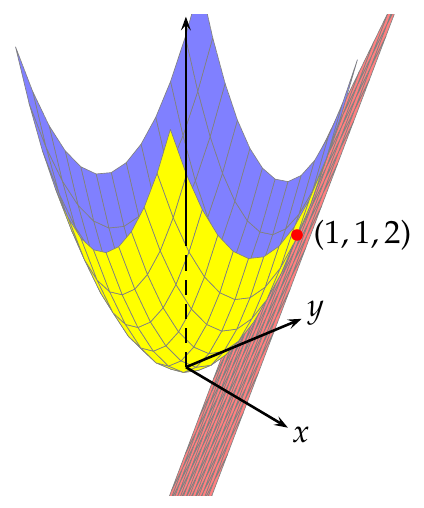
Derivadas parciales de segundo orden

Las derivadas parciales de una función son, a su vez, funciones de varias variables que muchas veces pueden volverse a derivar parcialmente con respecto a alguna de sus variables.

De forma análoga se definen las derivadas de orden superior.

Ejemplo. La función de dos variables $$f(x,y)=x^y$$ tiene cuatro derivadas parciales de segundo orden, que son:

$$\begin{aligned} \frac{\partial^2 f}{\partial x^2}(x,y) &= \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}(x,y)\right) = \frac{\partial}{\partial x}\left(yx^{y-1}\right) = y(y-1)x^{y-2},\newline \frac{\partial^2 f}{\partial y \partial x}(x,y) &= \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}(x,y)\right) = \frac{\partial}{\partial y}\left(yx^{y-1}\right) = x^{y-1}+yx^{y-1}\log x,\newline \frac{\partial^2 f}{\partial x \partial y}(x,y) &= \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}(x,y)\right) = \frac{\partial}{\partial x}\left(x^y\log x \right) = yx^{y-1}\log x+x^y\frac{1}{x},\newline \frac{\partial^2 f}{\partial y^2}(x,y) &= \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}(x,y)\right) = \frac{\partial}{\partial y}\left(x^y\log x \right) = x^y(\log x)^2.\end{aligned}$$

Matriz hessiana

Ejemplo. Consideremos de nuevo la función de dos variables $f(x,y)=x^y$. Su matriz hessiana es

$$\nabla^2f(x,y)=\left( \begin{array}{cc} \dfrac{\partial^2 f}{\partial x^2} & \dfrac{\partial^2 f}{\partial x \partial y}\newline \dfrac{\partial^2 f}{\partial y \partial x} & \dfrac{\partial^2 f}{\partial y^2} \end{array} \right)

\left( \begin{array}{cc} y(y-1)x^{y-2} & x^{y-1}(y\log x+1) \newline x^{y-1}(y\log x+1) & x^y(\log x)^2 \end{array} \right).$$

En el punto $(1,2)$ la matriz vale

$$\nabla^2f(1,2)=\left( \begin{array}{cc} 2(2-1)1^{2-2} & 1^{2-1}(2\log 1+1) \newline 1^{2-1}(2\log 1+1) & 1^2(\log 1)^2 \end{array} \right)

\left( \begin{array}{cc} 2 & 1 \newline 1 & 0 \end{array} \right).$$

Y el hessiano en dicho punto vale

$$Hf(1,2)=\left| \begin{array}{cc} 2 & 1 \newline 1 & 0 \end{array} \right|= 2\cdot 0-1\cdot1= -1. $$

Igualdad de las derivadas cruzadas

En el ejemplo anterior se aprecia que las derivadas cruzadas de segundo orden $\frac{\partial^2 f}{\partial y\partial x}$ y $\frac{\partial^2 f}{\partial x\partial y}$ coinciden. Ello es debido al siguiente teorema:

Teorema - Igualdad derivadas cruzadas. Si $f(x,y)$ es una función tal que sus derivadas parciales $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, $\frac{\partial^2 f}{\partial y\partial x}$ y $\frac{\partial^2 f}{\partial x\partial y}$ existen y son continuas en un conjunto abierto $A$, entonces

$$\frac{\partial^2 f}{\partial y\partial x}=\frac{\partial^2 f}{\partial x\partial y}.$$

Una consecuencia del teorema es que, al calcular una derivada parcial de segundo orden que cumpla lo anterior, ¡el orden en que se realicen las derivadas parciales no importa!

Si el teorema se cumple para todas las derivadas parciales de segundo orden, entonces la matriz hessiana es simétrica.

Fórmula de Taylor

Aproximación lineal de un campo escalar

Ya se vio cómo aproximar funciones de una variable mediante polinomios de Taylor. Esto también se puede generalizar a la aproximación de campos escalares mediante polinomios de varias variables.

Si $P$ es un punto del dominio de un campo escalar $f$ y $\mathbf{v}$ un vector, la fórmula de Taylor de primer grado de $f$ alrededor del punto $P$ es

$$f(P+\mathbf{v}) = f(P) + \nabla f(P)\cdot \mathbf{v} +R^1_{f,P}(\mathbf{v}),$$

donde

$$ \begin{aligned} P^1_{f,P}(\mathbf{v}) = f(P)+\nabla f(P)\mathbf{v} \end{aligned} $$

es el polinomio de Taylor de primer grado de $f$ en el punto $P$, y $R^1_{f,P}(\mathbf{v})$ es el resto de taylor para el vector $\mathbf{v}$, y mide el error cometido en la aproximación.

Se cumple que

$$\lim_{|\mathbf{v}|\rightarrow 0} \frac{R^1_{f,P}(\mathbf{v})}{|\mathbf{v}|} = 0$$

Obsérvese que el polinomio de Taylor de primer grado coincide con el plano tangente a $f$ en $P$.

Si $f$ es un campo escalar de dos variables $f(x,y)$ y $P=(x_0,y_0)$, teniendo en cuenta que para un punto cualquiera $Q=(x,y)$, el vector $\mathbf{v}=\vec{PQ}=(x-x_0,y-y_0)$, el polinomio de Taylor de $f$ en el punto $P$, puede expresarse

$$\begin{aligned} P^1_{f,P}(x,y) &= f(x_0,y_0)+\nabla f(x_0,y_0)(x-x_0,y-y_0) =\newline &= f(x_0,y_0)+\frac{\partial f}{\partial x}(x_0,y_0)(x-x_0)+\frac{\partial f}{\partial y}(x_0,y_0)(y-y_0). \end{aligned} $$

Ejemplo. Dado el campo escalar $f(x,y)=\log(xy)$, su gradiente es

$$\nabla f(x,y) = \left(\frac{1}{x},\frac{1}{y}\right),$$

y el polinomio de Taylor de primer grado en el punto $P=(1,1)$ es

$$ \begin{aligned} P^1_{f,P}(x,y) &= f(1,1) +\nabla f(1,1)\cdot (x-1,y-1) = \newline &= \log 1+(1,1)\cdot(x-1,y-1) = x-1+y-1 = x+y-2.\newline \end{aligned} $$

Este polinomio, permite aproximar el valor de $f$ cerca del punto $P$.

Por ejemplo

$$f(1.01,1.01) \approx P^1_{f,P}(1.01,1.01) = 1.01+1.01-2 = 0.02.$$

Aproximación cuadrática de un campo escalar

Si $P$ es un punto del dominio de un campo escalar $f$ y $\mathbf{v}$ un vector, la fórmula de Taylor de segundo grado de $f$ alrededor del punto $P$ es

$$f(P+\mathbf{v}) = f(P) + \nabla f(P)\cdot \mathbf{v} + \frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v} + R^2_{f,P}(\mathbf{v}),$$

donde

$$ \begin{aligned} P^2_{f,P}(\mathbf{v})&=f(P)+\nabla f(P)\mathbf{v}+\frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v} \end{aligned} $$

es el polinomio de Taylor de segundo grado de $f$ en el punto $P$, y $R^2_{f,P}(\mathbf{v})$ es el resto de taylor para el vector $\mathbf{v}$.

Se cumple que

$$\lim_{|\mathbf{v}\rightarrow 0|} \frac{R^2_{f,P}(\mathbf{v})}{|\mathbf{v}|^2} = 0$$

lo que indica que el resto es mucho más pequeño que el cuadrado del módulo de $\mathbf{v}$.

Si $f$ es un campo escalar de dos variables $f(x,y)$ y $P=(x_0,y_0)$, el polinomio de Taylor de $f$ en el punto $P$, puede expresarse

$$ \begin{gathered} P^2_{f,P}(x,y) = f(x_0,y_0)+\nabla f(x_0,y_0)(x-x_0,y-y_0) +\newline +\frac{1}{2}(x-x_0,y-y_0)\nabla^2f(x_0,y_0)(x-x_0,y-y_0)= \newline = f(x_0,y_0)+\frac{\partial f}{\partial x}(x_0,y_0)(x-x_0)+\frac{\partial f}{\partial y}(x_0,y_0)(y-y_0)+\newline +\frac{1}{2}\left(\frac{\partial^2 f}{\partial x^2}(x_0,y_0) (x-x_0)^2 + 2\frac{\partial^2 f}{\partial y\partial x}(x_0,y_0) (x-x_0)(y-y_0) + \frac{\partial^2 f}{\partial y^2}(x_0,y_0) (y-y_0)^2\right) \end{gathered} $$

Ejemplo. Dado el campo escalar $f(x,y)=\log(xy)$, su gradiente es

$$\nabla f(x,y) = \left(\frac{1}{x},\frac{1}{y}\right),$$

y su matriz hessiana es

$$Hf(x,y) = \left( \begin{array}{cc} \frac{-1}{x^2} & 0\newline 0 & \frac{-1}{y^2} \end{array} \right)$$

y el polinomio de Taylor de segundo grado en el punto $P=(1,1)$ es

$$ \begin{aligned} P^2_{f,P}(x,y) &= f(1,1) +\nabla f(1,1)\cdot (x-1,y-1) + \frac{1}{2}(x-1,y-1)\nabla^2f(1,1)\cdot(x-1,y-1)=\newline &= \log 1+(1,1)\cdot(x-1,y-1) + \frac{1}{2}(x-1,y-1) \left( \begin{array}{cc} -1 & 0\newline 0 & -1 \end{array} \right) \left( \begin{array}{c} x-1\newline y-1 \end{array} \right) = \newline &= x-1+y-1+\frac{-x^2-y^2+2x+2y-2}{2} = \frac{-x^2-y^2+4x+4y-6}{2}. \end{aligned} $$

Así, $$f(1.01,1.01) \approx P^1_{f,P}(1.01,1.01) = \frac{-1.01^2-1.01^2+4\cdot 1.01+4\cdot 1.01-6}{2} = 0.0199$$.

Extremos

Anulación del gradiente en los extremos

Si $P$ es un extremo de un campo escalar $f$ de $\mathbb{R}^n$, entonces $P$ es un punto crítico de $f$, es decir,

$$\nabla f(P) = 0.$$

Tomando la trayectoria que pasa por $P$ con la dirección y sentido del gradiente, $$g(t)=P+t\nabla f(P),$$ la función $h=(f\circ g)(t)$ nunca decrece ya que

$$h’(t)= (f\circ g)’(t) = \nabla f(g(t))\cdot g’(t) = \nabla f(P)\cdot \nabla f(P) = |\nabla f(P)|^2\geq 0.$$

y sólo se anula si $\nabla f(P)=0$.

Así pues, si $\nabla f(P)\neq 0$, entonces $P$ no puede ser un máximo ya que siguiendo la trayectoria de $g$ desde $P$ se encontrarían puntos en los que la imagen de $f$ es mayor que en $P$. Del mismo modo, siguiendo la trayectoria opuesta a $g$ se encontrarían puntos en los que la imagen de $f$ es menor que la imagen en $P$, por lo que tampoco puede ser un mínimo.

Ejemplo. Para el campo escalar $f(x,y)=x^2+y^2$, resulta evidente que sólo tiene un mínimo en el origen $(0,0)$ ya que

$$f(0,0)=0 \leq f(x,y)=x^2+y^2,\ \forall x,y\in \mathbb{R}.$$

En este punto se cumple, $\nabla f(0,0) = 0$.

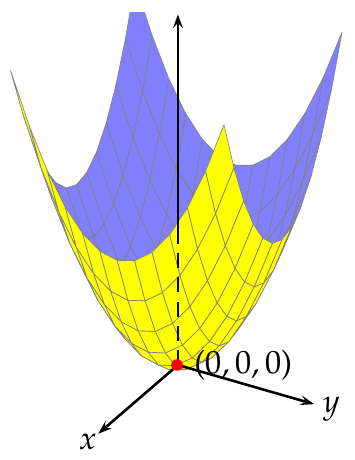
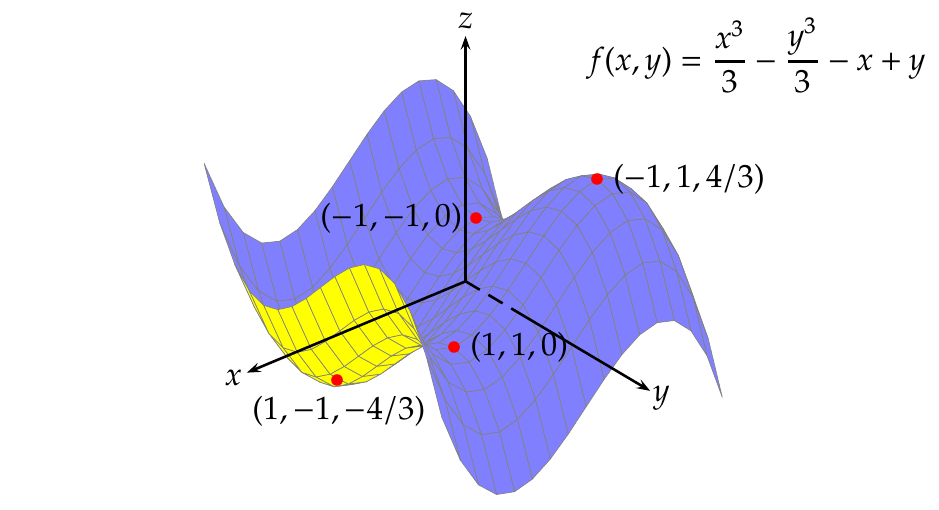
Puntos de silla

No todos los puntos críticos son extremos. Si se considera, por ejemplo, el campo escalar $f(x,y)=x^2-y^2$, su gradiente es

$$\nabla f(x,y) = (2x,-2y),$$

que sólo se anula en el punto $(0,0)$. Sin embargo, este punto no es un máximo relativo ya que los puntos $(x,0)$ del eje $X$ tienen imágenes $f(x,0)=x^2\geq 0=f(0,0)$, y tampoco es un mínimo relativo ya que los puntos $(0,y)$ del eje $Y$ tienen imágenes $f(0,y)=-y^2\leq 0=f(0,0)$. Este tipo de puntos que anulan el gradiente pero que no son extremos, se conocen como puntos de silla.

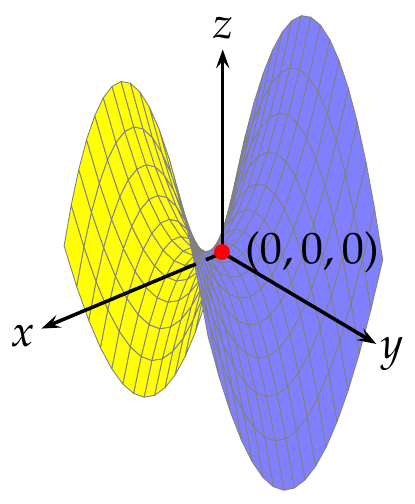
Determinación de los extremos de un campo escalar

De la fórmula de Taylor de segundo grado para un campo escalar $f$ en un punto $P$ se deduce que

$$f(P+\mathbf{v})-f(P)\approx \nabla f(P)\mathbf{v}+\frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}.$$

De manera que si $P$ es un punto crítico de $f$, como $\nabla f(P)=0$, se tiene que

$$f(P+\mathbf{v})-f(P)\approx \frac{1}{2}\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}.$$

Por tanto, el signo de $f(P+\mathbf{v})-f(P)$ coincide con el signo del término cuadrático $Hf(P)\mathbf{v}\cdot\mathbf{v}$.

Se pueden dar cuatro posibilidades:

• Definido positivo: $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}>0$ $\forall \mathbf{v}\neq 0$.
• Definido negativo: $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}<0$ $\forall \mathbf{v}\neq 0$.
• Indefinido: $\nabla^2f(P)\mathbf{v}\cdot\mathbf{v}>0$ para algún $\mathbf{v}\neq 0$ y $\nabla^2f(P)\mathbf{u}\cdot\mathbf{u}<0$ para algún $\mathbf{u}\neq 0$.
• Semidefinido: Cualquier otro caso distinto de los anteriores.

Así pues, dependiendo el signo de $Hf(P)\mathbf{v}\cdot\mathbf{v}$, se tiene

Teorema. Dado un punto crítico $P$ de un campo escalar $f$ que tiene matríz hessiana $Hf(P)$, se cumple

• Si $\nabla^2f(P)$ es definido positivo entonces $f$ tiene un mínimo relativo en $P$.
• Si $\nabla^2f(P)$ es definido negativo entonces $f$ tiene un máximo relativo en $P$.
• Si $\nabla^2f(P)$ es indefinido entonces $f$ tiene un punto de silla en $P$.

En el caso de que $\nabla^2f(P)$ sea semidefinido, no se puede obtener ninguna conclusión y hay que recurrir a derivadas parciales de orden superior.

En el caso particular de un campo escalar de dos variables se tiene

Teorema. Dado un punto crítico $P=(x_0,y_0)$ de un campo escalar $f(x,y)$ que tiene matríz hessiana $\nabla^2f(P)$, se cumple

• Si $Hf(P)>0$ y $\frac{\partial^2 f}{\partial x^2}(x_0,y_0)>0$ entonces $f$ tiene un mínimo relativo en $P$.
• Si $Hf(P)>0$ y $\frac{\partial^2 f}{\partial x^2}(x_0,y_0)<0$ entonces $f$ tiene un máximo relativo en $P$.
• Si $Hf(P)<0$ entonces $f$ tiene un punto de silla en $P$.

Ejemplo. Dada el campo escalar $f(x,y)=\dfrac{x^3}{3}-\dfrac{y^3}{3}-x+y$, se tiene que su gradiente vale

$$\nabla f(x,y)= (x^2-1,-y^2+1),$$

que se anula en los puntos $(1,1)$, $(1,-1)$, $(-1,1)$ y $(-1,-1)$.

La matriz hessiana vale

$$\nabla^2f(x,y) = \left( \begin{array}{cc} 2x & 0\newline 0 & -2y \end{array} \right)$$

y el hessiano vale

$$Hf(x,y) = -4xy.$$

Así pues, se tiene

• Punto $(1,1)$: $Hf(1,1)=-4<0 \Rightarrow$ Punto de silla.
• Punto $(1,-1)$: $Hf(1,-1)=4>0$ y $\frac{\partial^2}{\partial x^2}(1,-1)=2>0 \Rightarrow$ Mínimo relativo.
• Punto $(-1,1)$: $Hf(-1,1)=4>0$ y $\frac{\partial^2}{\partial x^2}(-1,1)=-2<0 \Rightarrow$ Máximo relativo.
• Punto $(-1,-1)$: $Hf(-1,-1)=-4<0 \Rightarrow$ Punto de silla.