2 Tipos de datos y variables

2.1 Tipos de datos numéricos

Enteros: Int64 (64 bits por defecto).
Racionales: Rational{Int64}. Utilizando el operador //.
Reales: Float64 (64 bits por defecto).
Complejos: Complex{Int64}. Utilizando im después de la parte imaginaria.

Para averiguar el tipo de un dato se utiliza la función typeof().

2.2 Ejemplos de tipos de datos numéricos

julia> typeof(3)
Int64

julia> typeof(3/2)
Float64

julia> typeof(3//2)
Rational{Int64}

julia> typeof(π)
Irrational{:π}

julia> typeof(3+2im)
Complex{Int64}

2.3 Jerarquía de tipos de datos numéricos

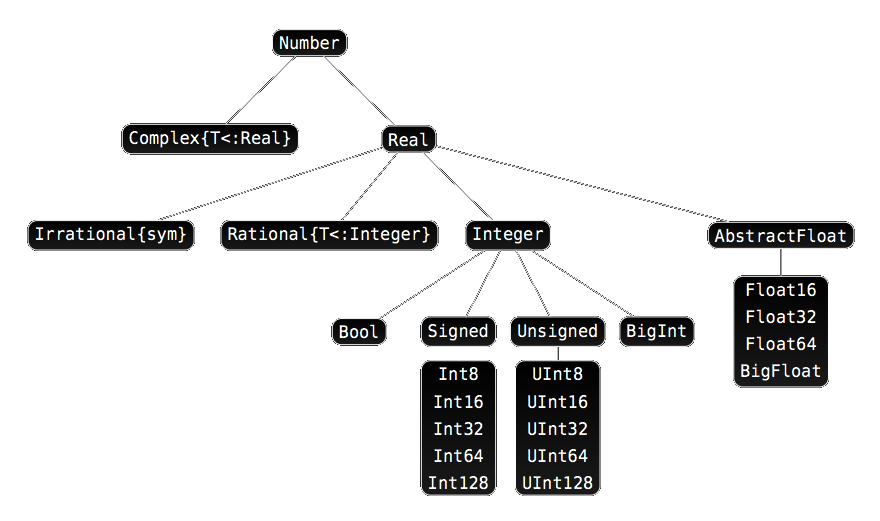
2.4 Constantes predefinidas

Símbolo	Descripción
`pi` o `π`	Número irracional $\pi$
`ℯ` (\euler + TAB)	Número irracional $e$
`Inf`	Infinito
`NaN`	Valor no numérico
`Missing`	Valor desconocido

2.5 Ejemplo de constantes predefinidas

julia> π
π = 3.1415926535897...

julia> 1 / 0
Inf

julia> 0 / 0
NaN

julia> Inf + Inf
Inf

julia> Inf - Inf
NaN

julia> 0 * Inf
NaN

2.6 Tipos de datos alfanuméricos

Caracteres: Char. Se representan entre comillas simples.
Cadenas: String. Se representan entre comillas dobles.

julia> typeof('a')
Char

julia> typeof("julia")
String

julia> typeof("a")
String

2.7 Tipo de datos booleanos

Booleanos: bool. Son un subtipo de los enteros Integer.

Solo contienen dos posibles valores: true (1) y false (0).

julia> typeof(true)
Bool

julia> typeof(false)
Bool

julia> typeof(1 < 2)
Bool

julia> true + true
2

2.8 Variables

Como lenguaje de tipado dinámico, no es necesario declarar una variable antes de usarla. Su tipo se infiere directamente del valor asociado.

julia> x = 1
1

julia> typeof(x)
Int64

julia> x = "julia"
"julia"

julia> typeof(x)
String

No obstante, para variables de ámbito local, por ejemplo en funciones, es posible fijar el tipo de una variable indicándolo detrás de su nombre con el operador ::.

x::Int64

2.9 Nombres de variables

Julia reconoce la codificación Unicode (UTF-8), lo que permite utilizar caracteres con tildes, letras griegas, símbolos matemáticos y hasta emoticonos en los nombres de variables o funciones. Para ello se utilizan códigos especiales (en muchos casos son los mismos que en LaTeX), pulsando después la tecla de tabulación.

julia> α = 1
1

julia> β = 2
2

julia> α + β
3

julia> 😄 = "julia"
"julia"

Distingue entre mayúsculas y minúsculas.

2.9.1 Caracteres Unicode

La siguiente tabla contiene algunos caracteres Unicode habituales

Código	Símbolo	Uso notes
`\euler`	`ℯ`	Constante de Euler `e`
`\pi`	`π`	Constante $pi$
`\alpha`	`α`
`\beta`	`β`
`\delta`	`δ`
`\Delta`	`Δ`	Variación
`\gamma`	`γ`
`\phi`	`ϕ`
`\Phi`	`Φ`
`x\_1`	`x₁`	Subíndices
`x\^2`	`x²`	Superíndices
`r\vec`	`r⃗`	Notación para vectores
`T\hat`	`T̂`	Notación para vectores unitarios
`\partial`	`∂`	Notación para derivadas parciales
`\nabla`	`∇`	Notación para el gradiente
`\circ`	`∘`	Operador de composición
`\cdot`	`⋅`	Operador de producto escalar
`\times`	`×`	Operador de producto vectorial

Los operadores pueden necesitar paréntesis, como por ejemplo (f ∘ g)(x) para la composición de g con f.

2.10 Operadores aritméticos

Operador	Descripción
`x + y`	Suma
`x - y`	Resta
`x * y`	Producto
`x / y`	División
`x ÷ y`	Cociente división entera
`x % y`	Resto división entera
`x ^ y`	Potencia

2.11 Operadores de comparación

Operador	Descripción
`==`	Igualdad
`!=`, `≠`	Desigualdad
`<`	Menor que
`<=`, `≤`	Menor o igual que
`>`	Mayor que
`>=`, `≥`	Mayor o igual que

2.12 Operadores booleanos

Operador	Descripción
`!x`	Negación
`x && y`	Conjunción (y)
`x \|\| y`	Disyunción (o)

2.13 Funciones numéricas predefinidas

2.13.1 Funciones de redondeo

Función	Descripción
`round(x)`	Devuelve el entero más próximo a `x`
`round(x, digits = n)`	Devuelve al valor más próximo a `x` con `n` decimales
`floor(x)`	Redondea `x` al próximo entero menor
`ceil(x)`	Redondea `x` al próximo entero mayor
`trunc(x)`	Devuelve la parte entera de `x`

2.13.2 Ejemplo de funciones de redondeo

julia> round(2.7)
3.0

julia> floor(2.7)
2.0

julia> floor(-2.7)
-3.0

julia> ceil(2.7)
3.0

julia> ceil(-2.7)
-2.0

julia> trunc(2.7)
2.0

julia> trunc(-2.7)
-2.0

julia> round(2.5)
2.0

julia> round(2.786, digits = 2)
2.79

2.13.3 Funciones de división

Función	Descripción
`div(x,y)`, `x÷y`	Cociente de la división entera
`fld(x,y)`	Cociente de la división entera redondeado hacia abajo
`cld(x,y)`	Cociente de la división entera redondeado hacia arriba
`rem(x,y)`, `x%y`	Resto de la división entera. Se cumple `x == div(x,y)*y + rem(x,y)`
`mod(x,y)`	Módulo con respecto a `y`. Se cumple `x == fld(x,y)*y + mod(x,y)`
`gcd(x,y...)`	Máximo común divisor positivo de `x`, `y`,…
`lcm(x,y...)`	Mínimo común múltiplo positivo de `x`, `y`,…

2.13.4 Ejemplo de funciones de división

julia> div(5,3)
1

julia> cld(5,3)
2

julia> 5%3
2

julia> -5%3
-2

julia> mod(5,3)
2

julia> mod(-5,3)
1

julia> gcd(12,18)
6

julia> lcm(12,18)
36

2.13.5 Funciones para el signo y el valor absoluto

Función	Descripción
`abs(x)`	Valor absoluto de `x`
`sign(x)`	Devuelve 1 si `x` es positivo, -1 si es negativo y 0 si es 0.

julia> abs(2.5)
2.5

julia> abs(-2.5)
2.5

julia> sign(-2.5)
-1.0

julia> sign(0)
0

julia> sign(2.5)
1.0

2.13.6 Raíces, exponenciales y logaritmos

Función	Descripción
`sqrt(x)`, `√x`	Raíz cuadrada de `x`
`cbrt(x)`, `∛x`	Raíz cúbica de `x`
`exp(x)`	Exponencial de `x`
`log(x)`	Logaritmo neperiano de `x`
`log(b,x)`	Logaritmo en base `b` de `x`
`log2(x)`	Logaritmo en base 2 de `x`
`log10(x)`	Logaritmo en base 10 de `x`

2.13.7 Ejemplo de raíces, exponenciales y logaritmos

julia> sqrt(4)
2.0

julia> cbrt(27)
3.0

julia> exp(1)
2.718281828459045

julia> exp(-Inf)
0.0

julia> log(1)
0.0

julia> log(0)
-Inf

julia> log(-1)
ERROR: DomainError with -1.0:
log will only return a complex result if called with a complex argument.
...

julia> log(-1+0im)
0.0 + 3.141592653589793im

julia> log2(2^3)
3.0

2.13.8 Funciones trigonométricas

Función	Descripción
`hypot(x,y)`	Hipotenusa del triángulo rectángulo con catetos `x` e `y`
`sin(x)`	Seno del ángulo `x` en radianes
`sind(x)`	Seno del ángulo `x` en grados
`cos(x)`	Coseno del ángulo `x` en radianes
`cosd(x)`	Coseno del ángulo `x` en grados
`tan(x)`	Tangente del ángulo `x` en radianes
`tand(x)`	Tangente del ángulo `x` en grados
`sec(x)`	Secante del ángulo `x` en radianes
`csc(x)`	Cosecante del ángulo `x` en radianes
`cot(x)`	Cotangente del ángulo `x` en radianes

2.13.9 Ejemplo de funciones trigonométricas

julia> sin(π/2)
1.0

julia> cos(π/2)
6.123233995736766e-17

julia> cosd(90)
0.0

julia> tan(π/4)
0.9999999999999999

julia> tand(45)
1.0

julia> tan(π/2)
1.633123935319537e16

julia> tand(90)
Inf

julia> sin(π/4)^2 + cos(π/4)^2
1.0

2.13.10 Funciones trigonométricas inversas

Función	Descripción
`asin(x)`	Arcoseno (inversa del seno) de `x` en radianes
`asind(x)`	Arcoseno (inversa del seno) de `x` en grados
`acos(x)`	Arcocoseno (inversa del coseno) de `x` en radianes
`acosd(x)`	Arcocoseno (inversa del coseno) de `x` en grados
`atan(x)`	Arcotangente (inversa de la tangente) de `x` en radianes
`atand(x)`	Arcotangente (inversa de la tangente) de `x` en grados
`asec(x)`	Arcosecante (inversa de la secante) de `x` en radianes
`acsc(x)`	Arcocosecante (inversa de la cosecante) de `x` en radianes
`acot(x)`	Arcocotangente (inversa de la cotangente) de `x` en radianes

2.13.11 Ejemplo de funciones trigonométricas inversas

julia> asin(1)
1.5707963267948966

julia> asind(1)
90.0

julia> acos(-1)
3.141592653589793

julia> atan(1)
0.7853981633974483

julia> atand(tan(π/4))
45.0

2.14 Precedencia de operadores

De mayor a menor prioridad.

Categoría	Operadores	Asociatividad
Exponenciación	`^`	Derecha
Unarios	`+ - √`	Derecha
Fracciones	`//`	Izquierda
Multiplicación	`* / % & \ ÷`	Izquierda
Adición	`+ - \|`	Izquierda
Comparaciones	`> < >= <= == != !==`
Asignaciones	`= += -= *= /= //= ^= ÷= %= \|= &=`	Derecha

2.15 Operaciones con cadenas

Las cadenas son secuencias de caracteres alfanuméricos del tipo char entre dobles comillas.

Cada carácter tiene asociado un índice entero. El primer carácter de la cadena tiene índice 1.

Índice	1	2	3	4	5
Cadena	j	u	l	i	a

Podemos acceder a cada carácter usando su índice entre corchetes a continuación de la cadena:

s[i]: Devuelve el carácter con índice i en la cadena s.

julia> c = "julia"
"julia"

julia> c[2]
'u': ASCII/Unicode U+0075 (category Ll: Letter, lowercase)

2.15.1 Acceso a caracteres Unicode

Sin embargo, como Julia permite caracteres Unicode, el índice de un carácter en una cadena, no siempre se corresponde con su posición en la cadena. Ello es debido a que la codificación UTF-8 no utiliza el mismo número de bytes para representar los caracteres Unicode. Mientras que los caracteres habituales del código ASCII (letras romanas y números árabes) solo necesitan un byte, otros caracteres como los símbolos matemáticos requieren más.

Índice	1	4	5	6	9
Cadena	∀	x		∃	y

2.15.2 Ejemplo de acceso a caracteres Unicode

julia> c = "∀x ∃y"
"∀x ∃y"

julia> c[1]
'∀': Unicode U+2200 (category Sm: Symbol, math)

julia> c[2]
ERROR: StringIndexError: invalid index [2], 
valid nearby indices [1]=>'∀', [4]=>'x'
Stacktrace:
 [1] string_index_err(s::String, i::Int64)
   @ Base ./strings/string.jl:12
 [2] getindex_continued(s::String, i::Int64, u::UInt32)
   @ Base ./strings/string.jl:233
 [3] getindex(s::String, i::Int64)
   @ Base ./strings/string.jl:226
 [4] top-level scope
   @ REPL[128]:1

2.15.3 Acceso a índices en cadenas

Las siguientes funciones permiten acceder a los índices de una cadena:

firstindex(c): Devuelve el índice del primer carácter de la cadena c.
lastindex(c): Devuelve el índice del primer carácter de la cadena c.
nextind(c, i): Devuelve el índice del carácter de la cadena c que sigue al carácter con índice i.
prevind(c, i): Devuelve el índice del carácter de la cadena c que sigue al carácter con índice i.

2.15.4 Ejemplo de acceso a índices en cadenas

julia> firstindex(c)
1

julia> lastindex(c)
9

julia> c[9]
'y': ASCII/Unicode U+0079 (category Ll: Letter, lowercase)

julia> nextind(c,1)
4

julia> prevind(c, lastindex(c))
6

2.15.5 Subcadenas

Para obtener subcadenas se usan también los corchetes indicando los índices de inicio y fin separados por :.

s[i:j]: Devuelve la subcadena que va desde el índice i al índice j, ambos incluidos.

También se pueden obtener subcadenas con la siguiente función:

SubString(s, i, j): Devuelve la subcadena que va desde el índice i al índice j, ambos incluidos.

julia> c = "julia"
"julia"

julia> c[2:4]
"uli"

julia> SubString(c, 2, 4)
"uli"

2.16 Concatenación de cadenas

a * b: Devuelve la cadena que resulta de concatenar las cadenas a y b.
a ^ i: Devuelve la cadena que resulta de repetir la cadena a el número de veces i.
repeat(a, i): Devuelve la cadena que resulta de repetir la cadena a el número de veces i.

julia> a = "Hola"
"Hola"

julia> b = "Julia"
"Julia"

julia> a * b
"HolaJulia"

julia> b ^ 3
"JuliaJuliaJulia"

2.16.1 Interpolación de cadenas

En una cadena se pueden introducir variables o expresiones precedidas del símbolo $, de manera que al evaluarlas julia sustituye la variable o expresión por su valor. Esto es muy util para formatear salidas.

julia> "1 + 2 = $(1 + 2)"
"1 + 2 = 3"

julia> s = "Julia"
"Julia"

julia> "Hola $s"
"Hola Julia"

2.16.2 Otras operaciones comunes con cadenas

length(c): Devuelve el número de caracteres de la cadena c.
findfirst(a, c): Devuelve el índice de la primera ocurrencia de la cadena a en la cadena c. Si a no es una subcadena de c devuelve nada (tipo Nothing).
findlast(a, c): Devuelve el índice de la última ocurrencia de la cadena a en la cadena c. Si a no es una subcadena de c devuelve nada (tipo Nothing).
findnext(a, c, i): Devuelve el índice de la primera ocurrencia de la cadena a en la cadena c posterior al índice i.
findprev(a, c, i): Devuelve el índice de la última ocurrencia de la cadena a en la cadena c anterior al índice i.

2.16.3 Otras operaciones comunes con cadenas

occursin(a, c): Devuelve true si la cadena a es una subcadena de c, y false en caso contrario.
contains(c, a): Devuelve true si la cadena a es una subcadena de c, y false en caso contrario.
replace(c, a => b): Devuelve la cadena que resulta de sustituir la cadena a por la b en la cadena c.
lowercase(c): Devuelve la cadena c en minúsculas.
uppercase(c): Devuelve la cadena c en mayúsculas.
prefix(c, a): Devuelve true si la cadena a es un prefijo de la cadena c.
suffix(c, a): Devuelve true si la cadena a es un sufijo de la cadena c.
split(c, a): Devuelve una lista con las cadenas que resulpan de partir la cadena c por el delimitador a.

2.16.4 Ejemplo de otras operaciones con cadenas

julia> c = "Hola Julia"
"Hola Julia"

julia> length(c)
10

julia> findfirst("a", c) 
4:4

julia> findlast("Ju", c)
6:7

julia> findlast("x", c)

julia> occursin("Julia", c)
true

julia> occursin("julia", c)
false

julia> replace(c, "a" => "o")
"Holo Julio"

julia> uppercase(c)
"HOLA JULIA"

julia> split(c, " ")
2-element Vector{SubString{String}}:
 "Hola"
 "Julia"

2.17 Entrada y salida por terminal

Las siguientes funciones muestran una cadena en la terminal:

print(c): Muestra por la terminal la cadena c sin cambiar de línea.
println(c): Muestra por la terminal la cadena c y cambia de línea.

La siguiente función permite leer una línea de texto desde la terminal:

readline(): Devuelve en una cadena una línea de texto introducida por el usuario en la terminal (hasta el carácter de cambio de línea \n)

julia> print("¿Cómo te llamas?")
¿Cómo te llamas?
julia> nombre = readline()
Alf            
"Alf"

julia> println("Hola $nombre")
Hola Alf

2.17.1 Conversión de cadenas en números

La función readline() siempre devuelve una cadena aún cuando se pregunte al usuario por un valor numérico. Para convertir una cadena en un dato numérico se utiliza la siguiente función:

parse(tipo, c): Covierte la cadena c a un número del tipo numérico tipo, siempre que puedad realizarse la conversión.

julia> print("Introduce tu edad")
Introduce tu edad
julia> edad = parse(Int, readline())
18
18

julia> println("Vas a cumplir $(edad + 1) años")
Vas a cumplir 19 años

julia> typeof(edad)
Int64