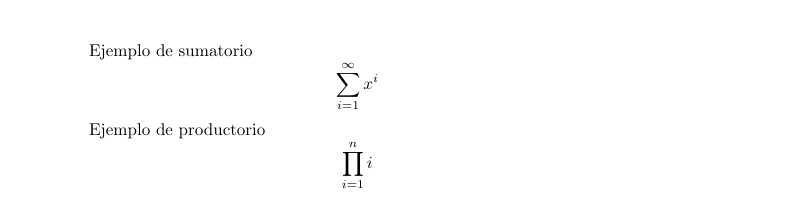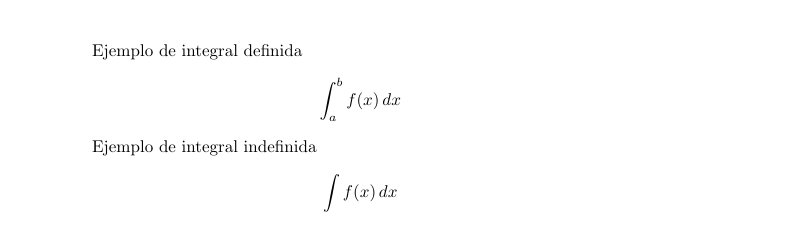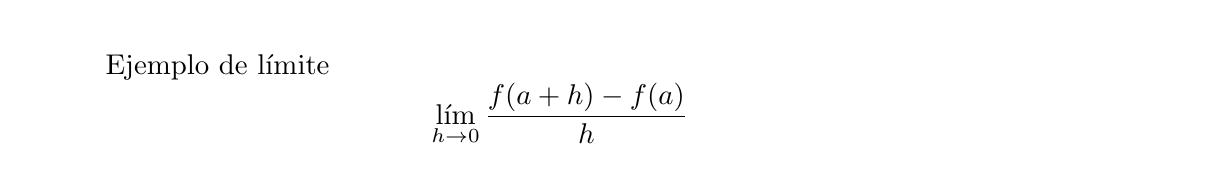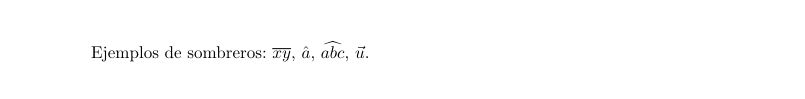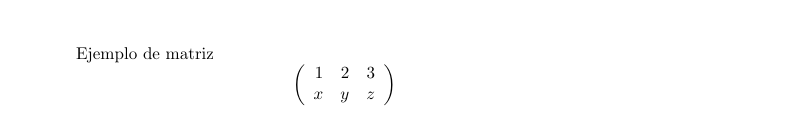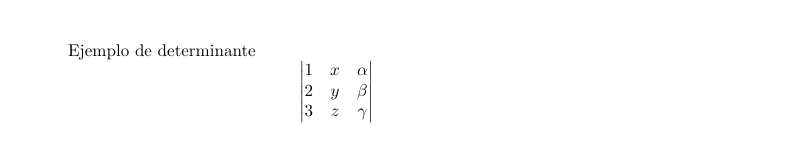8 Fórmulas matemáticas

La escritura de fórmulas matemáticas es uno de los puntos fuertes de , y es por ello que se utiliza tanto para la creación de documentos científicos o técnicos con contenido matemático.

Para escribir una fórmula es necesario cambiar al modo matemático. Existen distintas formas de activar el modo matemático:

$: Activa el modo matemático en linea, es decir, las fórmulas aparecerán en la misma linea que el texto que las rodea. Para desactivar este modo hay que volver a escriri $.
$$: Activa el modo matemático display (desplegado), de manera que las fórmulas aparecen en una línea aparte.
El entorno equation también activa el modo matemático display pero además asigna un número a la ecuación, para poder referenciarla en otras partes del documento.

Ejemplo 8.1

% CUERPO
\begin{document}
Ejemplo de fórmula en linea $ x+y=0 $.

Ejemplo de fórmula desplegada

$$ 
x+y=0
$$
Ejemplo de fórmula con el entorno \texttt{equation}

\begin{equation}
x+y=0
\end{equation}
\end{document}

Salida

8.1 Símbolos matemáticos

Existe una infinidad de símbolos matemáticos que escriben mediante comandos. A continuación se muestran los más habituales.¹

8.1.1 Letras griegas

Para escribir letras griegas se utilizan los siguientes comandos:

Minúsculas

`\alpha` $\alpha$	`\theta` $\theta$	o $o$	`\tau` $\tau$
`\beta` $\beta$	`\vartheta` $\vartheta$	`\pi` $\pi$	`\upsilon` $\upsilon$
`\gamma` $\gamma$	`\iota` $\iota$	`\varpi` $\varpi$	`\phi` $\phi$
`\delta` $\delta$	`\kappa` $\kappa$	`\rho` $\rho$	`\varphi` $\varphi$
`\epsilon` $\epsilon$	`\lambda` $\lambda$	`\varrho` $\varrho$	`\chi` $\chi$
`\varepsilon` $\varepsilon$	`\mu` $\mu$	`\sigma` $\sigma$	`\psi` $\psi$
`\zeta` $\zeta$	`\nu` $\nu$	`\varsigma` $\varsigma$	`\omega` $\omega$
`\eta` $\eta$	`\xi` $\xi$

Mayúsculas

`\Gamma` $\Gamma$	`\Lambda` $\Lambda$	`\Sigma` $\Sigma$	`\Psi` $\Psi$
`\Delta` $\Delta$	`\Xi` $\Xi$	`\Upsilon` $\Upsilon$	`\Omega` $\Omega$
`\Theta` $\Theta$	`\Pi` $\Pi$	`\Phi` $Phi$

8.1.2 Operadores aritméticos

`+` $+$	`-` $-$	`\times` $\times$	`\cdot` $\cdot$
`/` $/$	`\div` $\div$	`\sqrt{...}` $\sqrt{}$	`\pm` $\pm$

8.1.3 Relaciones

`=` $=$	`\neq` $\neq$	`<` $<$	`\leq` $\leq$
`>` $>$	`\geq` $\geq$	`\approx` $\approx$	`\sim` $\sim$
`\equiv` $\equiv$	`\in` $\in$	`\not\in` $\not\in$	`\subset` $\subset$
`\not\subset` $\not\subset$	`\subseteq` $\subseteq$	`\subsetneq` $\subsetneq$

8.1.4 Operadores binarios

\cup $\cup$ \cap $\cap$ \setminus $\setminus$ \circ $\circ$

8.1.5 Lógica

\exists $\exists$ \forall $\forall$ \neg $\neg$ \lor $\lor$ \land $\land$

8.1.6 Conjuntos

`\emptyset` $\emptyset$	`\mathbb{N}` $\mathbb{N}$	`\mathbb{Z}` $\mathbb{Z}$	`\mathbb{Q}` $\mathbb{Q}$
`\mathbb{R}` $\mathbb{R}$	`\mathbb{C}` $\mathbb{C}$

8.1.7 Flechas

`\rightarrow` $\to$	`\Rightarrow` $\Rightarrow$	`\longrightarrow` $\longrightarrow$	`\Longrightarrow` $\Longrightarrow$
`\leftarrow` $\leftarrow$	`\Leftarrow` $\Leftarrow$	`\longleftarrow` $\longleftarrow$	`\Longleftarrow` $\Longleftarrow$
`\leftrightarrow` $\leftrightarrow$	`\Leftrightarrow` $\Leftrightarrow$	`\longleftrightarrow` $\longleftrightarrow$	`\Longleftrightarrow` $\Longleftrightarrow$
`\uparrow` $\uparrow$	`\Uparrow` $\Uparrow$	`\downarrow` $\downarrow$	`\Downarrow` $\Downarrow$
`\updownarrow` $\updownarrow$	`\Updownarrow` $\Updownarrow$

8.1.8 Puntos suspensivos

\ldots $\ldots$ \cdots $\cdots$ \vdots $\vdots$ \ddots $\ddots$

8.1.9 Otros símbolos

\infty $\infty$ \partial $\partial$ \nabla $\nabla$

8.1.10 Funciones

`\sin` $\sin$	`\arcsin` $\arcsin$	`\csc` $\csc$	`\operatorname{arccsc}` $\operatorname{arccsc}$
`\cos` $\cos$	`\arccos` $\arccos$	`\sec` $\sec$	`\operatorname{arcsec}` $\operatorname{arcsec}$
`\tan` $\tan$	`\arctan` $\arctan$	`\cot` $\cot$	`\operatorname{arccot}` $\operatorname{arccot}$
`\exp` $\exp$	`\log` $\log$	`\ln` $\ln$

Es posible declarar nuevos operadores o funciones cargando el paquete amsmath con el comando \DeclareMathOperator{comando}{texto}. Por ejemplo, para obtener las versión de la función seno en español se puede definir DeclareMathOperator{\sen}{sen} en el preámbulo y luego utilizar el comando \sen en el cuerpo para obtener la función seno en español.

Otro paquete que incorpora aún más símbolos es amssymb.

8.2 Subíndices y superíndices

Para poner subíndices se utiliza el comando _ y para superíndices ^. Si el subíndice o superíndice afecta a más de un carácter, hay que ponerlos entre llaves.

Ejemplo 8.2

% CUERPO
\begin{document}
Ejemplo de fórmula con subíndices

$$ 
x_i+y_j=0
$$

Ejemplo de fórmula con superíndices

$$ 
x^2+y^2=0
$$

Ejemplo de fórmula con subíndices y superíndices

$$ 
x_i^2+y_j^2=0
$$

\end{document}

Salida

Se pueden escribir subíndices de subíndices o superíndices de superíndices anidando los comandos.

8.3 Fracciones

Para escribir fracciones simples en línea se puede usar el operador aritmético $/$ (por ejemplo $3/4$), pero para fracciones más complejas o fracciones en modo display, conviene utilizar el comando \frac{num}{den}, donde num es el numerador y den el denominador.

A su vez, se pueden escribir más fracciones en el numerador o el denominador, anidando este comando.

Ejemplo 8.3

% CUERPO
\begin{document}
Ejemplo de fracción en línea $\frac{x+2}{x^2-2x+1}$.

Ejemplo de fracción en modo desplegado

$$
\frac{\frac{x}{2}+\frac{2}{3}}{x^2-2x+1}
$$

\end{document}

Salida

8.4 Sumatorios, productorios, integrales y límites.

Para escribir sumatorios se utiliza el comando \sum_{sub}^{sup}, donde sub es el subíndice que indica el inicio de la suma y sup es el superíndice que indica el final de la suma. Si se quieren omitir los índices de inicio y final de la suma, basta con el comando \sum.

De manera análoga, para escribir productorios se utiliza el comando \prod_{sub}^{sup}, donde sub es el subíndice que indica el inicio del producto y sup es el superíndice que indica el final del producto. Si se quieren omitir los índices de inicio y final del producto, basta con el comando \prod.

Ejemplo 8.4

% CUERPO
\begin{document}
Ejemplo de sumatorio
$$
\sum_{i=1}^{\infty} x^i
$$

Ejemplo de productorio
$$
\prod_{i=1}^n i
$$
\end{document}

Salida

Del mismo modo, para escribir integrales definidas se utiliza el comando \int_{sub}^{sup}, donde sub es el subíndice que indica el inicio de la integral y sup es el superíndice que indica el final de la integral. Para integrales indefinidas, basta con el comando \int.

Ejemplo 8.5

% CUERPO
\begin{document}
Ejemplo de integral definida
$$
\int_a^b f(x)\,dx
$$

Ejemplo de integral indefinida
$$
\int f(x)\,dx
$$
\end{document}

Salida

Finalmente, para escribir límites se utiliza el comando \lim_{sub}, donde sub es el subíndice e indica las variables y el valor al que tienden.

Ejemplo 8.6

% CUERPO
\begin{document}
Ejemplo de límite
$$
\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}
$$
\end{document}

Salida

8.5 Sombreros

Es posible poner símbolos encima de otros símbolos, más conocidos como sombreros. Los siguientes comandos sirven para poner distintos tipos de sombreros:

\bar{...}: Linea horizontal para un carácter.
\overline{...}: Línea horizontal para varios caracteres.
\hat: Ángulo para un carácter.
\widehat: Ángulo para varios caracteres.
\vec{...}: Flecha para un carácter.
\overrightarrow{...}: Flecha para varios caracteres.

Ejemplo 8.7

% CUERPO
\begin{document}
Ejemplos de sombreros: $\overline{xy}$, $\hat{a}$, $\widehat{abc}$, $\vec{u}$.
\end{document}

Salida

8.6 Matrices

Las matrices se crean de manera similar a como se crean las tablas (ver Capítulo 6), pero utilizando el entorno array en lugar del entorno tabular. Para encerrar la matriz entre paréntesis se pone el comando \left( antes del entorno y el comando \right) después.

Ejemplo 8.8

% CUERPO
\begin{document}
Ejemplo de matriz
$$
\left(
\begin{array}{rrr}
1 & 2 & 3 \\
x & y & z \\
\end{array}
\right)
$$
\end{document}

Salida

El paquete amsmath incorpora varios entornos más específicos para matrices donde no es necesario especificar el número de columnas, y tampoco los delimitadores:

matrix: Matriz sin delimitadores (equivalente al entorno array)
pmatrix: Matriz encerrada entre paréntesis.
vmatrix: Matriz encerrada entre barras verticales (por ejemplo para determinates).
Vmatrix: Matriz encerrada ente dobles barras verticales.
bmatrix: Matriz encerrada entre corchetes.
Bmatrix: Matriz encerrada entre llaves.

Ejemplo 8.9

% PREÁMBULO
\usepackage{amsmath}
% CUERPO
\begin{document}
Ejemplo de determinante

$$
\begin{vmatrix}
1 & x & \alpha \\
2 & y & \beta \\
3 & z &\gamma
\end{vmatrix}
$$
\end{document}

Salida

8.7 Teoremas

Para crear denificiones, teoremas, proposiciones, corolarios y otros tipos de enunciados de sebe cargar el paquete amsthm y definir los tipos de enunciados en el preámbulo con el comando \newtheorem{entorno}{texo}, donde entorno es el nombre del entorno y texto el texto que aparerá en el documento final como encabezado del enunciado.

Estos entornos admiten como argumento opcional un texto que se utiliza para dar nombre al enunciado.

Los enunciados definidos con este comando aparecen por defecto numerados para poder referenciarlos en otras partes del documento, pero se pueden definir entornos no numerados con la variante del comando anterior \newtheorem*{entorno}{texo}

Para demostraciones se puede utilizar el entorno proof.

Ejemplo 8.10

% PREÁMBULO
\usepackage{amsmath}
\DeclareMathOperator{\sen}{sen}
\usepackage{amsthm}
\newtheorem{midef}{Definición}
\newtheorem{teo}{Teorema}

% CUERPO
\begin{document}

\begin{midef}
Dado un triángulo rectángulo de catetos $a$, $b$ e hipotenusa $c$, se define
el seno del ángulo $\alpha$ opuesto al cateto $b$ como 

$$
\sen{\alpha}= \frac{b}{c}.
$$
\end{midef}

\begin{teo}
Para cualquier ángulo $\alpha$ se cumple 
$\sen(\alpha)^2 + \cos(\alpha)^2 = 1$.
\end{teo}

\begin{proof}
Es una consecuencia directa del teorema de Pitágoras.
\end{proof}
\end{document}

Salida

Tip

Se recomienda cargar los paquetes amsmath, amssymb y amsthm para documentos extensos o con muchas fórmulas matemáticas.

Para un listado más exhaustivo de los símbolos matemáticos de , puede consultarse el documento The Great, Big List of Symbols.↩︎

`\alpha` \(\alpha\)	`\theta` \(\theta\)	o \(o\)	`\tau` \(\tau\)
`\beta` \(\beta\)	`\vartheta` \(\vartheta\)	`\pi` \(\pi\)	`\upsilon` \(\upsilon\)
`\gamma` \(\gamma\)	`\iota` \(\iota\)	`\varpi` \(\varpi\)	`\phi` \(\phi\)
`\delta` \(\delta\)	`\kappa` \(\kappa\)	`\rho` \(\rho\)	`\varphi` \(\varphi\)
`\epsilon` \(\epsilon\)	`\lambda` \(\lambda\)	`\varrho` \(\varrho\)	`\chi` \(\chi\)
`\varepsilon` \(\varepsilon\)	`\mu` \(\mu\)	`\sigma` \(\sigma\)	`\psi` \(\psi\)
`\zeta` \(\zeta\)	`\nu` \(\nu\)	`\varsigma` \(\varsigma\)	`\omega` \(\omega\)
`\eta` \(\eta\)	`\xi` \(\xi\)

`\Gamma` \(\Gamma\)	`\Lambda` \(\Lambda\)	`\Sigma` \(\Sigma\)	`\Psi` \(\Psi\)
`\Delta` \(\Delta\)	`\Xi` \(\Xi\)	`\Upsilon` \(\Upsilon\)	`\Omega` \(\Omega\)
`\Theta` \(\Theta\)	`\Pi` \(\Pi\)	`\Phi` \(Phi\)

`+` \(+\)	`-` \(-\)	`\times` \(\times\)	`\cdot` \(\cdot\)
`/` \(/\)	`\div` \(\div\)	`\sqrt{...}` \(\sqrt{}\)	`\pm` \(\pm\)

`=` \(=\)	`\neq` \(\neq\)	`<` \(<\)	`\leq` \(\leq\)
`>` \(>\)	`\geq` \(\geq\)	`\approx` \(\approx\)	`\sim` \(\sim\)
`\equiv` \(\equiv\)	`\in` \(\in\)	`\not\in` \(\not\in\)	`\subset` \(\subset\)
`\not\subset` \(\not\subset\)	`\subseteq` \(\subseteq\)	`\subsetneq` \(\subsetneq\)

`\emptyset` \(\emptyset\)	`\mathbb{N}` \(\mathbb{N}\)	`\mathbb{Z}` \(\mathbb{Z}\)	`\mathbb{Q}` \(\mathbb{Q}\)
`\mathbb{R}` \(\mathbb{R}\)	`\mathbb{C}` \(\mathbb{C}\)

`\rightarrow` \(\to\)	`\Rightarrow` \(\Rightarrow\)	`\longrightarrow` \(\longrightarrow\)	`\Longrightarrow` \(\Longrightarrow\)
`\leftarrow` \(\leftarrow\)	`\Leftarrow` \(\Leftarrow\)	`\longleftarrow` \(\longleftarrow\)	`\Longleftarrow` \(\Longleftarrow\)
`\leftrightarrow` \(\leftrightarrow\)	`\Leftrightarrow` \(\Leftrightarrow\)	`\longleftrightarrow` \(\longleftrightarrow\)	`\Longleftrightarrow` \(\Longleftrightarrow\)
`\uparrow` \(\uparrow\)	`\Uparrow` \(\Uparrow\)	`\downarrow` \(\downarrow\)	`\Downarrow` \(\Downarrow\)
`\updownarrow` \(\updownarrow\)	`\Updownarrow` \(\Updownarrow\)

`\sin` \(\sin\)	`\arcsin` \(\arcsin\)	`\csc` \(\csc\)	`\operatorname{arccsc}` \(\operatorname{arccsc}\)
`\cos` \(\cos\)	`\arccos` \(\arccos\)	`\sec` \(\sec\)	`\operatorname{arcsec}` \(\operatorname{arcsec}\)
`\tan` \(\tan\)	`\arctan` \(\arctan\)	`\cot` \(\cot\)	`\operatorname{arccot}` \(\operatorname{arccot}\)
`\exp` \(\exp\)	`\log` \(\log\)	`\ln` \(\ln\)