7 Intervalos de confianza para medias y proporciones de una población

7.1 Ejercicios Resueltos

Para la realización de esta práctica se requieren los siguientes paquetes:

library(tidyverse)
# Incluye los siguientes paquetes:
# - dplyr: para el preprocesamiento y manipulación de datos.
# - ggplot2: para la representación gráfica.
# - purrr: para aplicar funciones a vectores.
library(broom) # para convertir las listas con los resúmenes de los modelos de regresión a formato organizado.
library(tidymodels) # para realizar contrastes de hipótesis en formato tidy.
library(samplingbook) # para el cálculo de tamaños muestrales.
library(knitr) # para el formateo de tablas.

Ejercicio 7.1 Se sabe que para que un fármaco sea efectivo, la concentración de su principio activo debe ser de al menos $16$ mg/mm$^3$. Una farmacia va a comprar un lote de este medicamento, pero antes quiere asegurarse de que los medicamentos del lote son efectivos y para ello analiza la concentración de principio activo en una muestra aleatoria de $10$ envases tomados del lote, obteniendo los siguientes resultados en mg/mm$^{3}$:

\[ 17.6 \quad 19.2 \quad 21.3 \quad 15.1 \quad 17.6 \quad 18.9 \quad 16.2 \quad 18.3 \quad 19.0 \quad 16.4 \]

Crear un conjunto de datos con los datos de la muestra.

Solución

df <- data.frame(concentracion = c(17.6, 19.2, 21.3, 15.1, 17.6, 18.9, 16.2, 18.3, 19.0, 16.4 ))

Calcular la concentración media de principio activo de la muestra. ¿Puede afirmarse que los medicamentos del lote son efectivos?
Solución
mean(df$concentracion)

[1] 17.96
A pesar de la concentración media está por encima de $16$ mg/mm$^3$, se trata de una estimación puntual, y por tanto, no podemos garantizar que la media poblacional esté por encima de $16$ mg/mm$^3$. ¿Puede afirmarse con este nivel de confianza que los medicamentos del lote son efectivos?
Calcular el intervalo de confianza para la media de la concentración del lote con nivel de confianza del $95\%$ (nivel de significación $\alpha =0.05$). ¿Puede afirmarse ahora que los medicamentos del lote son efectivos?

Ayuda

Para calcular el intervalo de confianza para la media de una población podemos utilizar la función t.test del paquete stats.

Si queremos mostrar la salida del test en formato de tabla podemos utilizar la función tidy del paquete broom.

También podemos usar la función t_test de la colección de paquetes tidymodels, que ofrece ya la salida en formato tidy.
Solución
stats

tidymodels

t1 <- t.test(df$concentracion) t1$conf.int

[1] 16.68158 19.23842 attr(,"conf.level") [1] 0.95

Para mostrar la salida en formato de tabla.

library(tidyverse) library(broom) library(knitr) tidy(t1) |> select(estimate, conf.low, conf.high) |> kable()

estimate conf.low conf.high

17.96 16.68158 19.23842

library(tidymodels) df |> t_test(response = concentracion) |> select(estimate, lower_ci, upper_ci) |> kable()

estimate lower_ci upper_ci

17.96 16.68158 19.23842
Como el intervalo entero está por encima de $16$ mg/mm$^3$, podemos afirmar con una confianza del $95\%$ que la concentración media de principio activo del lote está por encima de $16$ mg/mm$^3$ y por tanto podemos concluir que los medicamentos del lote son efectivos.
¿Puede afirmarse que los medicamentos del lote son efectivos con un $99\%$ de confianza?
Solución
t2 <- t.test(df$concentracion, conf.level = 0.99) t2$conf.int

[1] 16.1234 19.7966 attr(,"conf.level") [1] 0.99
Como el intervalo entero sigue estando por encima de $16$ mg/mm$^3$, podemos afirmar con una confianza del $99\%$ que los medicamentos del lote son efectivos.
Si definimos la precisión del intervalo como la inversa de su amplitud, ¿cómo afecta a la precisión del intervalo de confianza el tomar niveles de significación cada vez más altos? ¿Cuál puede ser la explicación?
Solución
cat(paste0("Amplitud intervalo 95%: ", t1$conf.int[2] - t1$conf.int[1]))

Amplitud intervalo 95%: 2.55684921520655

cat(paste0("Amplitud intervalo 99%: ", t2$conf.int[2] - t2$conf.int[1]))

Amplitud intervalo 99%: 3.67319282263829
Como se ve, al aumentar el nivel de confianza del intervalo, la precisión disminuye. Ello es debido a que para tener más confianza de capturar el verdadero valor de la media en el intervalo, debemos hacer mayor el intervalo.
¿Qué tamaño muestral sería necesario para obtener una estimación del contenido medio de principio activo con un margen de error de $\pm 0.5$ mg/mm$^3$ y una confianza del 95%?
Solución
El tamaño muestral necesario para construir un intervalo de confianza para la media depende del nivel de confianza deseado ($0.95$ en este caso), del error o semiamplitud del intervalo deseado ($0.5$ en este caso) y de la desviación típica poblacional, que no se conoce, pero se puede estimar mediante la cuasidesviación típica muestral.
library(samplingbook) sample.size.mean(e = 0.5, S = sd(df$concentracion), level = 0.95)

sample.size.mean object: Sample size for mean estimate Without finite population correction: N=Inf, precision e=0.5 and standard deviation S=1.7871 Sample size needed: 50

estimate	conf.low	conf.high
17.96	16.68158	19.23842

estimate	lower_ci	upper_ci
17.96	16.68158	19.23842

Ejercicio 7.2 Una central de productos lácteos recibe diariamente la leche de dos granjas $X$ e $Y$. Para analizar la calidad de la leche, durante una temporada, se controla el porcentaje de materia grasa de la leche que proviene de ambas granjas, con los siguientes resultados:

\[ \begin{array}{c|c} X & Y \\ \hline \begin{array}[t]{rr} 3.4 & 3.4 \\ 3.2 & 3.5 \\ 3.3 & 3.3 \\ 3.2 & 3.2 \\ 3.3 & 3.0 \\ 3.1 & 3.2 \\ \end{array} & \begin{array}[t]{rr} 2.8 & 2.9 \\ 3.0 & 3.2 \\ 3.2 & 3.1 \\ 2.9 & 2.9 \\ 3.1 & 3.2 \\ 2.9 & 3.1 \\ 3.3 & 3.2 \\ 3.2 & 3.3 \\ \end{array} \end{array} \]

Crear un conjunto de datos con los datos de la muestra.

Solución

library(tidyverse)
df <- tibble(
    grasa = c(3.4, 3.2, 3.3, 3.2, 3.3, 3.1, 3.4, 3.5, 3.3, 3.2, 3.0, 3.2, 2.8, 3.0, 3.2, 2.9, 3.1, 2.9, 3.3, 3.2, 2.9, 3.2, 3.1, 2.9, 3.2, 3.1, 3.2, 3.3),
    granja = factor(c(rep("X", 12), rep("Y", 16)))
)

Calcular el contenido medio de materia grasa de la muestra de leche cada granja y los respectivos intervalos de confianza con un $95\%$ de confianza. Dibujar los intervalos de confianza obtenidos.

Ayuda

Para calcular el intervalo de confianza para la media de una población podemos utilizar la función t.test del paquete stats.

También podemos usar la función t_test de la colección de paquetes tidymodels, que ofrece ya la salida en formato tidy.

Otra opción es utilizar la función mean_ci del paquete qwraps2.

Solución

stats
tidymodels

library(knitr)
df |> 
    group_by(granja) |>
    summarise("Media" = mean(grasa, na.rm = T), 
    "IC 95% Inf" = t.test(grasa)$conf.int[1], 
    "IC 95% Sup" = t.test(grasa)$conf.int[2]) |> 
    kable()

granja	Media	IC 95% Inf	IC 95% Sup
X	3.258333	3.170719	3.345948
Y	3.081250	2.995950	3.166550

Otra opción es anidando los data frames de cada granja y aplicar el test t para cada grupo.

tabla_ic <- df |> 
    nest(data = -granja) |> 
    mutate(test = map(data, ~ tidy(t.test(.x$grasa)))) |> 
    unnest(test) |> 
    select(granja, estimate, conf.low, conf.high) 

tabla_ic |> 
    kable()

granja	estimate	conf.low	conf.high
X	3.258333	3.170719	3.345948
Y	3.081250	2.995950	3.166550

library(tidymodels)
df |> 
    nest(data = -granja) |> 
    mutate(test = map(data, ~ t_test(x = .x, response = grasa))) |> 
    unnest(test) |> 
    select(granja, estimate, lower_ci, upper_ci) |> 
    kable()

granja	estimate	lower_ci	upper_ci
X	3.258333	3.170719	3.345948
Y	3.081250	2.995950	3.166550

Ahora dibujamos los intervalos de confianza.

tabla_ic  |> 
    ggplot(aes(x = granja, y = estimate, color = granja)) +
    geom_point(size = 3) +
    geom_errorbar(aes(ymin = conf.low, ymax = conf.high), width = 0.2) +
    labs(title = "Intervalos de confianza del 95% para la media", x = "Granja", y = "Porcentaje de grasa")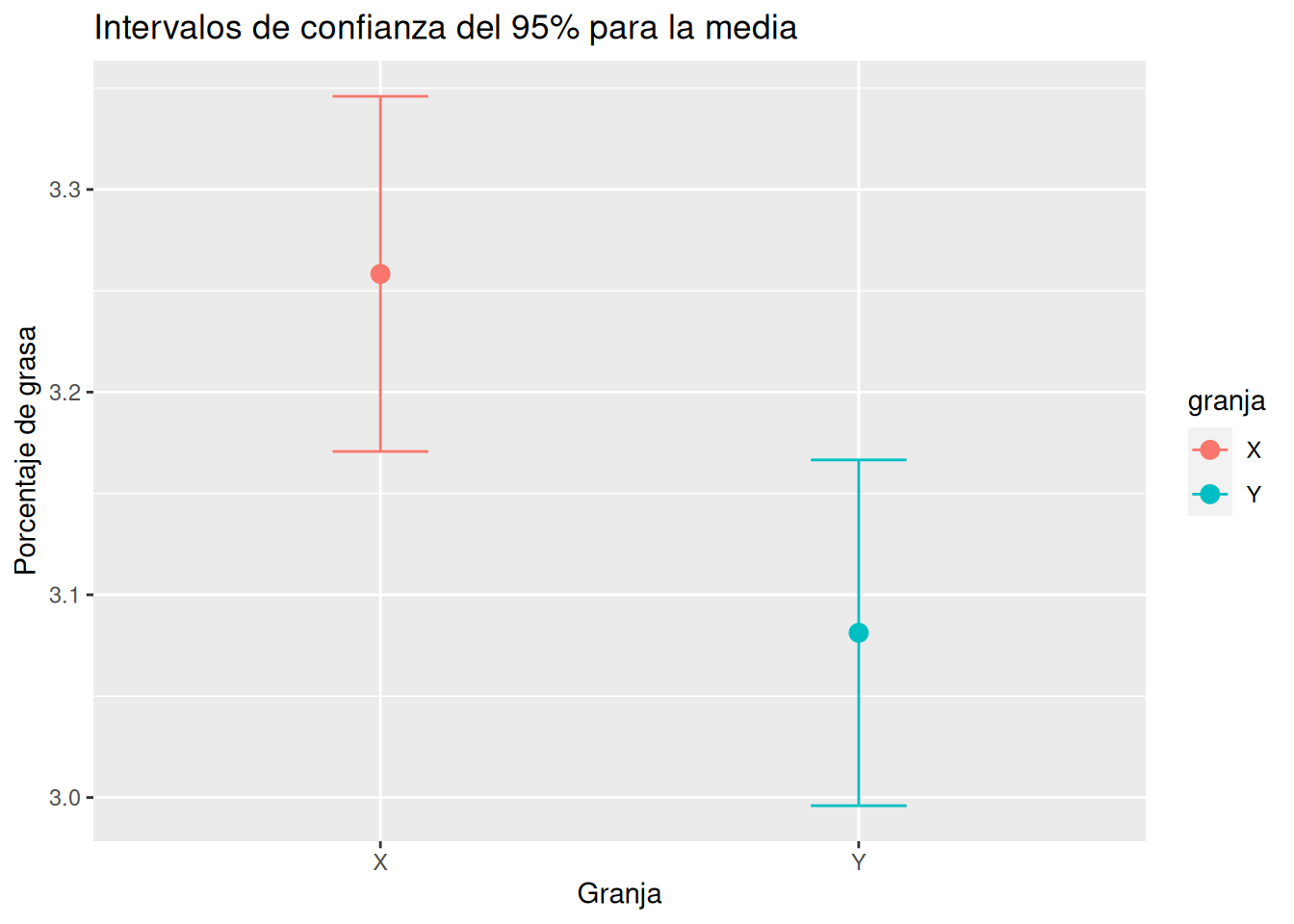

A la vista de los intervalos de confianza obtenidos ¿Existen diferencias estadísticamente significativas entre los contenidos medios de grasa de la leche de las dos granjas? En tal caso, ¿qué granja produce leche con más grasa?

Solución

Como los intervalos no se solapan, es decir, no tienen valores en común, podemos concluir que los contenidos medios de grasa de las leches de las dos granjas son significativamente diferentes con un $95\%$ de confianza. Además se aprecia que el intervalo de la granja $X$ tiene valores mayores que el de la granja $Y$, por lo que la leche de la granja $X$ tiene más contenido de grasa que la de la granja $Y$.

Repetir los cálculos anteriores tomando una confianza del $99\%$. ¿Existen diferencias estadísticamente significativas entre el contenido medio de grasa de las leches de las dos granjas con este nivel de confianza?

Solución

stats
tidymodels

tabla_ic_99 <- df |> 
    nest(data = -granja) |> 
    mutate(test = map(data, ~ tidy(t.test(.x$grasa, conf.level = 0.99)))) |> 
    unnest(test) |> 
    select(granja, estimate, conf.low, conf.high) 

tabla_ic_99 |> 
    kable()

granja	estimate	conf.low	conf.high
X	3.258333	3.134701	3.381966
Y	3.081250	2.963324	3.199176

library(tidymodels)
df |> 
    nest(data = -granja) |> 
    mutate(test = map(data, ~ t_test(x = .x, response = grasa, conf_level = 0.99))) |> 
    unnest(test) |> 
    select(granja, estimate, lower_ci, upper_ci) |> 
    kable()

granja	estimate	lower_ci	upper_ci
X	3.258333	3.134701	3.381966
Y	3.081250	2.963324	3.199176

Ahora dibujamos los intervalos de confianza.

tabla_ic_99  |> 
    ggplot(aes(x = granja, y = estimate, color = granja)) +
    geom_point(size = 3) +
    geom_errorbar(aes(ymin = conf.low, ymax = conf.high), width = 0.2) +
    labs(title = "Intervalos de confianza del 99% para la media", x = "Granja", y = "Porcentaje de grasa")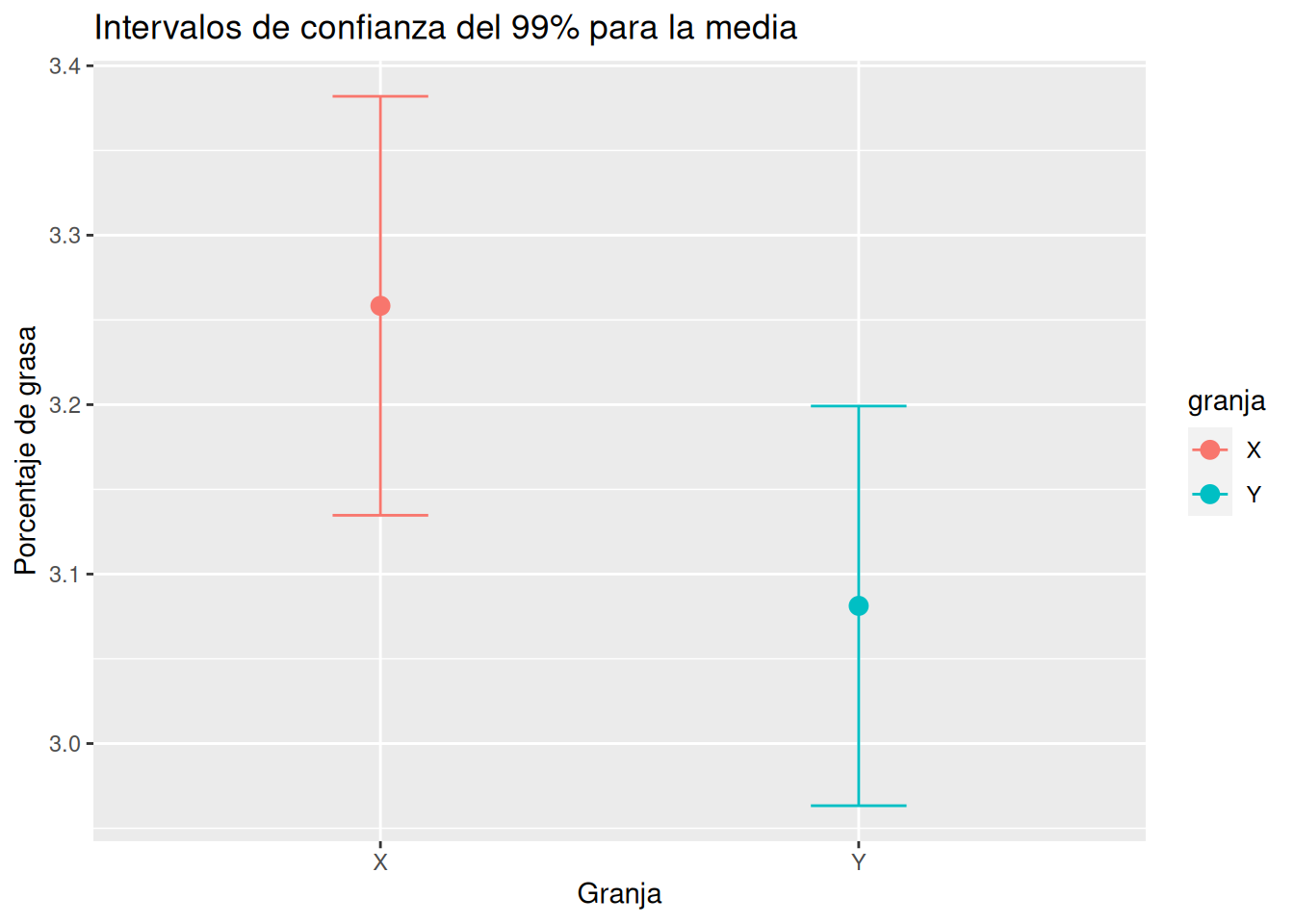

Como se ve, ahora los dos intervalos se solapan y por tanto las medias del contenido de grasa de las leches de las dos granjas podrían ser iguales. Por tanto, no existen diferencias estadísticamente significativas entre el contenido medio de grasa de las leches de las dos granjas con un $99º%$ de confianza.

Ejercicio 7.3 El conjunto de datos biblioteca.csv contiene los resultados de una encuesta realizada en una universidad, sobre si el alumnado utiliza habitualmente (al menos una vez a la semana) la biblioteca.

Crear conjunto de datos con los datos de la muestra a partir del fichero biblioteca.csv.

Solución

library(tidyverse)
df <- read_csv("https://aprendeconalf.es/estadistica-practicas-r/datos/biblioteca.csv")

Calcular el intervalo de confianza con $\alpha=0.01$ para la proporción del alumnado que utiliza habitualmente la biblioteca. ¿Cómo es la precisión del intervalo?

Ayuda

Para calcular el intervalo de confianza para la proporción de una población podemos utilizar la función prop.test del paquete stats.

Si queremos mostrar la salida del test en formato de tabla podemos utilizar la función tidy del paquete broom.

También podemos usar la función prop_test de la colección de paquetes tidymodels, que ofrece ya la salida en formato tidy.
Solución
stats

tidymodels

library(broom) library(knitr) frec <- table(df$respuesta) tidy(prop.test(frec["si"], nrow(df), conf.level = 0.99)) |> select(estimate, conf.low, conf.high) |> kable()

estimate conf.low conf.high

0.4705882 0.261705 0.6896622

library(tidymodels) library(knitr) df |> prop_test(response = respuesta, conf_level = 0.99) |> mutate(estimate = nrow(df[df$respuesta == "si", ]) / nrow(df)) |> select(estimate, lower_ci, upper_ci) |> kable()

estimate lower_ci upper_ci

0.4705882 0.3103378 0.738295
Se trata de un intervalo poco preciso, ya que su amplitud es bastante grande.
¿Qué tamaño muestral sería necesario para obtener una estimación de la proporción de alumnos que utilizan regularmente la biblioteca con un margen de error de un $1\%$ y una confianza del $95\%$?
Solución
El tamaño muestral necesario para construir un intervalo de confianza para la media depende del nivel de confianza deseado ($0.95$ en este caso), del error o semiamplitud del intervalo deseado ($0.01$ en este caso) y de proporción poblacional, que no se conoce, pero se puede estimar mediante la proporción muestral.
library(samplingbook) sample.size.prop(e = 0.01, P = frec["si"]/nrow(df), level = 0.95)

sample.size.prop object: Sample size for proportion estimate Without finite population correction: N=Inf, precision e=0.01 and expected proportion P=0.4706 Sample size needed: 9571
Calcular los intervalo de confianza para las proporciones de chicas y chicos que utilizan regularmente la biblioteca. ¿Existe una diferencia estadísticamente significativa entre la proporción de chicas y chicos que utilizan regularmente la biblioteca? En tal caso, ¿quiénes utilizan más la biblioteca?
Solución
stats

tidymodels

df |> group_by(sexo) |> count(respuesta) |> mutate(test = map(n, \(x) tidy(prop.test(x, sum(n))))) |> unnest(test) |> filter(respuesta == "si") |> select(sexo, respuesta, n, estimate, conf.low, conf.high) |> kable()

sexo respuesta n estimate conf.low conf.high

H si 3 0.1875000 0.0497313 0.4630766

M si 13 0.7222222 0.4640580 0.8928742

df |> nest(data = -sexo) |> mutate(test = map(data, ~ prop_test(x = .x, response = respuesta, success = "si"))) |> mutate(estimate = map(data, ~ nrow(.x[.x$respuesta == "si", ]) / nrow(.x))) |> unnest(c(test, estimate)) |> select(sexo, estimate, lower_ci, upper_ci) |> kable()

No `p` argument was hypothesized, so the test will assume a null hypothesis `p = .5`. No `p` argument was hypothesized, so the test will assume a null hypothesis `p = .5`.

sexo estimate lower_ci upper_ci

H 0.1875000 0.0497313 0.4630766

M 0.7222222 0.4640580 0.8928742
Como los intervalos de confianza para las proporciones de chicos y chicas que utilizan regularmente la biblioteca no se solapan, es decir, no tienen valores en común, podemos concluir que existe una diferencia estadísticamente significativa entre ambas proporciones con un $95\%$ de confianza. Como además el intervalo de confianza para la proporción de chicas está claramente por encima del de chicos, se concluye que hay más chicas utilizan regularmente la biblioteca.

estimate	conf.low	conf.high
0.4705882	0.261705	0.6896622

estimate	lower_ci	upper_ci
0.4705882	0.3103378	0.738295

sexo	respuesta	n	estimate	conf.low	conf.high
H	si	3	0.1875000	0.0497313	0.4630766
M	si	13	0.7222222	0.4640580	0.8928742

sexo	estimate	lower_ci	upper_ci
H	0.1875000	0.0497313	0.4630766
M	0.7222222	0.4640580	0.8928742

Ejercicio 7.4 En un sondeo preelectoral se ha tomado una muestra de $500$ personas y se ha observado que $220$ votarían al partido $A$ y $180$ votarían al partido $B$.

Calcular el intervalo de confianza para el porcentaje de voto al partido $A$.

Solución

library(broom)
library(knitr)
tidy(prop.test(220, 500)) |> 
select(estimate, conf.low, conf.high) |> 
mutate(across(everything(), ~ .x * 100)) |> 
kable()

estimate	conf.low	conf.high
44	39.613	48.48059

Calcular el intervalo de confianza para el porcentaje de voto al partido $B$.

Solución

tidy(prop.test(180, 500)) |> 
select(estimate, conf.low, conf.high) |> 
mutate(across(everything(), ~ .x * 100)) |> 
kable()

estimate	conf.low	conf.high
36	31.81744	40.40109

A la vista de los intervalos de confianza, ¿se puede asegurar con un $95\%$ de confianza qué partido ganará las elecciones?

Solución

Como ambos intervalos se solapan, no existe una diferencia estadísticamente significativa entre los porcentajes de votos a ambos partidos, y por tanto, no se puede asegurar con un $95\%$ de confianza qué partido ganará las elecciones.

7.2 Ejercicios propuestos

Ejercicio 7.5 El conjunto de datos neonatos contiene información sobre una muestra de 320 recién nacidos en un hospital durante un año que cumplieron el tiempo normal de gestación.

Calcular el intervalo de confianza del $99\%$ para el peso medio de los recién nacidos. ¿Entre qué valores estará el peso medio?
Calcular el intervalo de confianza para la puntuación media del Apgar al minuto de nacer y compararlo con el de la puntuación Apgar a los 5 minutos. ¿Existe una diferencia estadísticamente significativa entre las medias de las dos puntuaciones?
Calcular el intervalo de confianza para el porcentaje de niños con peso menor o igual que $2.5$ Kg en el grupo de las madres que han fumado durante el embarazo y en el de las que no. ¿Podemos afirmar con un $95\%$ de confianza que el que la madre fume influye significativamente en el peso de los recién nacidos?

Ejercicio 7.6 En una fábrica de componentes electrónicos, hay dos máquinas que producen un mismo tipo de chips. Se ha tomado una muestra de chips de cada máquina y se ha observado que en la primera máquina hubo 12 chips defectuosos de un total de 200, mientras que en la segunda máquina hubo un total de 10 chips defectuosos de un total de 300. ¿Se puede afirmar con un $90\%$ de confianza que la segunda máquina produce menos chips defectuosos que la primera?