Regression

In the last chapter we saw how to describe the distribution of a single variable in a sample. However, in most cases, studies require to describe several variables that are often related. For instance, a nutritional study should consider all the variables that could be related to the weight, as height, age, gender, smoking, diet, physic exercise, etc.

To understand a phenomenon that involve several variables is not enough to study every variable by its own. We have to study all the variables together to describe how they interact and the type of relation among them.

Usually in a dependency study there is a dependent variable $Y$ that it is supposed to be influenced by a set of variables $X_1,\dots ,X_n$ known as independent variables. The simpler case is a simple dependency study when there is only one independent variable, that is the case covered in this chapter.

Joint distribution

Joint frequencies

To study the relation between two variables $X$ and $Y$, we have to study the joint distribution of the two-dimensional variable $(X,Y)$, whose values are pairs $(x_i,y_j)$ where the first element is a value of $X$ and the second a value of $Y$.

Joint frequency distribution

The values of the two-dimensional variable with their frequencies is known as joint frequency distribution, and is represented in a joint frequency table.

$$\begin{array}{|cccccc|}\hline X\mathrm{\setminus }Y& y_1& \cdots & y_j& \cdots & y_q\\ x_1& n_{11}& \cdots & n_{1j}& \cdots & n_{1q}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_i& n_{i1}& \cdots & n_{ij}& \cdots & n_{iq}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_p& n_{p1}& \cdots & n_{pj}& \cdots & n_{pq}\\ \hline\end{array}$$

Example (grouped data). The height (in cm) and weight (in kg) of a sample of 30 students is:

The joint frequency table is

$$\begin{array}{|ccccccc|}\hline X/Y& [50,60)& [60,70)& [70,80)& [80,90)& [90,100)& [100,110)\\ (150,160]& 2& 0& 0& 0& 0& 0\\ (160,170]& 4& 4& 0& 0& 0& 0\\ (170,180]& 1& 6& 3& 1& 0& 0\\ (180,190]& 0& 1& 4& 1& 1& 0\\ (190,200]& 0& 0& 0& 0& 1& 1\\ \hline\end{array}$$

Scatter plot

The joint frequency distribution can be represented graphically with a scatter plot, where data is displayed as a collections of points on a $XY$ coordinate system.

Usually the independent variable is represented in the $X$ axis and the dependent variable in the $Y$ axis. For every data pair $(x_i,y_j)$ in the sample a dot is drawn on the plane with those coordinates.

The result is a set of points that usually is known as a point cloud.

Example. The scatter plot below represent the distribution of heights and weights of the previous sample.

The shape of the point cloud in a scatter plot gives information about the type of relation between the variables.

Marginal frequency distributions

The frequency distributions of each variable of the two-dimensional variable are known as marginal frequency distributions.

We can get the marginal frequency distributions from the joint frequency table by adding frequencies by rows and columns.

$$\begin{array}{|ccccccc|}\hline X\mathrm{\setminus }Y& y_1& \cdots & y_j& \cdots & y_q& n_x\\ x_1& n_{11}& \cdots & n_{1j}& \cdots & n_{1q}& n_{x_1}\\ ⋮& ⋮& ⋮& \downarrow +& ⋮& ⋮& ⋮\\ x_i& n_{i1}& \stackrel{+}{\to }& n_{ij}& \stackrel{+}{\to }& n_{iq}& n_{x_i}\\ ⋮& ⋮& ⋮& \downarrow +& ⋮& ⋮& ⋮\\ x_p& n_{p1}& \cdots & n_{pj}& \cdots & n_{pq}& n_{x_p}\\ n_y& n_{y_1}& \cdots & n_{y_j}& \cdots & n_{y_q}& n\\ \hline\end{array}$$

Example. The marginal frequency distributions for the previous sample of heights and weights are

$$\begin{array}{|cccccccc|}\hline X/Y& [50,60)& [60,70)& [70,80)& [80,90)& [90,100)& [100,110)& n_x\\ (150,160]& 2& 0& 0& 0& 0& 0& 2\\ (160,170]& 4& 4& 0& 0& 0& 0& 8\\ (170,180]& 1& 6& 3& 1& 0& 0& 11\\ (180,190]& 0& 1& 4& 1& 1& 0& 7\\ (190,200]& 0& 0& 0& 0& 1& 1& 2\\ n_y& 7& 11& 7& 2& 2& 1& 30\\ \hline\end{array}$$

and the corresponding statistics are

$$\begin{array}{lllll}\overline{x}=174.67\text{ cm}& & s_x^2=102.06{\text{ cm}}^2& & s_x=10.1\text{ cm}\\ \overline{y}=69.67\text{ Kg}& & s_y^2=164.42{\text{ Kg}}^2& & s_y=12.82\text{ Kg}\end{array}$$

Covariance

To study the relation between two variables, we have to analyze the joint variation of them.

Dividing the point cloud of the scatter plot in 4 quadrants centered in the mean point $(\overline{x},\overline{y})$, the sign of deviations from the mean is:

If there is an increasing linear relationship between the variables, most of the points will fall in quadrants 1 and 3, and the sum of the products of deviations from the mean will be positive.

$$\sum (x_i-\overline{x})(y_j-\overline{y})>0$$

If there is an decreasing linear relationship between the variables, most of the points will fall in quadrants 2 and 4, and the sum of the products of deviations from the mean will be negative.

$$\sum (x_i-\overline{x})(y_j-\overline{y})<0$$

Using the products of deviations from the means we get the following statistic.

It can also be calculated using the formula

$$s_{xy}=\frac{\sum x_i{y}_j{n}_{ij}}{n}-\overline{x}\overline{y}.$$

Example. Using the joint frequency table of the sample of heights and weights

$$\begin{array}{|cccccccc|}\hline X/Y& [50,60)& [60,70)& [70,80)& [80,90)& [90,100)& [100,110)& n_x\\ (150,160]& 2& 0& 0& 0& 0& 0& 2\\ (160,170]& 4& 4& 0& 0& 0& 0& 8\\ (170,180]& 1& 6& 3& 1& 0& 0& 11\\ (180,190]& 0& 1& 4& 1& 1& 0& 7\\ (190,200]& 0& 0& 0& 0& 1& 1& 2\\ n_y& 7& 11& 7& 2& 2& 1& 30\\ \hline\end{array}$$

$$\overline{x}=174.67\text{ cm}\overline{y}=69.67\text{ Kg}$$

we get that the covariance is equal to

$$\begin{array}{rl}{s}_{xy}& =\frac{\sum x_i{y}_j{n}_{ij}}{n}-\overline{x}\overline{y}=\frac{155\cdot 55\cdot 2+165\cdot 55\cdot 4+\cdots +195\cdot 105\cdot 1}{30}-174.67\cdot 69.67=\\ & =\frac{368200}{30}-12169.26=104.07\text{ cm}\cdot \text{ Kg}.\end{array}$$

This means that there is a increasing linear relation between the weight and the height.

Regression

In most cases the goal of a dependency study is not only to detect a relation between two variables, but also to express that relation with a mathematical function, $$y=f(x)$$ in order to predict the dependent variable for every value of the independent one. The part of Statistics in charge of constructing such a function is called regression, and the function is known as regression function or regression model.

Simple regression models

There are a lot of types of regression models. The most common models are shown in the table below.

The model choice depends on the shape of the points cloud in the scatterplot.

Residuals or predictive errors

Once chosen the type of regression model, we have to determine which function of that family explains better the relation between the dependent and the independent variables, that is, the function that predicts better the dependent variable.

That function is the function that minimizes the distances from the observed values for $Y$ in the sample to the predicted values of the regression function. These distances are known as residuals or predictive errors.

Least squares fitting

A way to get the regression function is the least squares method, that determines the function that minimizes the squared residuals.

$$\sum e_{ij}^2.$$

For a linear model $f(x)=a+bx$, the sum depends on two parameters,the intercept $a$, and the slope $b$ of the straight line,

$$\theta (a,b)=\sum e_{ij}^2=\sum (y_j-f(x_i){)}^2=\sum (y_j-a-b{x}_i{)}^2.$$

This reduces the problem to determine the values of $a$ and $b$ that minimize this sum.

To solve the minimization problem, we have to set to zero the partial derivatives with respect to $a$ and $b$.

$$\begin{array}{rl}\frac{\partial \theta (a,b)}{\partial a}& =\frac{\partial \sum (y_j-a-b{x}_i{)}^2}{\partial a}=0\\ \frac{\partial \theta (a,b)}{\partial b}& =\frac{\partial \sum (y_j-a-b{x}_i{)}^2}{\partial b}=0\end{array}$$

And solving the equation system, we get

$$a=\overline{y}-\frac{s_{xy}}{s_x^2}\overline{x}b=\frac{s_{xy}}{s_x^2}$$

This values minimize the residuals on $Y$ and give us the optimal linear model.

Regression line

Example. Using the previous sample of heights ($X$) and weights ($Y$) with the following statistics

$$\begin{array}{lllll}\overline{x}=174.67\text{ cm}& & s_x^2=102.06{\text{ cm}}^2& & s_x=10.1\text{ cm}\\ \overline{y}=69.67\text{ Kg}& & s_y^2=164.42{\text{ Kg}}^2& & s_y=12.82\text{ Kg}\\ & & s_{xy}=104.07\text{ cm}\cdot \text{ Kg}& & \end{array}$$

the regression line of weight on height is

$$y=\overline{y}+\frac{s_{xy}}{s_x^2}(x-\overline{x})=69.67+\frac{104.07}{102.06}(x-174.67)=-108.49+1.02x$$

And the regression line of height on weight is

$$x=\overline{x}+\frac{s_{xy}}{s_y^2}(y-\overline{y})=174.67+\frac{104.07}{164.42}(y-69.67)=130.78+0.63y$$

Relative position of the regression lines

Usually, the regression line of $Y$ on $X$ and the regression line of $X$ on $Y$ are not the same, but they always intersect in the mean point $(\overline{x},\overline{y})$.

If there is a perfect linear relation between the variables, then both regression lines are the same, as that line makes both $X$-residuals and $Y$-residuals zero.

If there is no linear relation between the variables, then both regression lines are constant and equals to the respective means,

$$y=\overline{y},x=\overline{x}.$$

So, they intersect perpendicularly.

Regression coefficient

The most important parameter of a regression line is the slope.

Example. In the sample of heights and weights, the regression line of weight on height was

$$y=-108.49+1.02x.$$

Thus, the regression coefficient of weight on height is

$$b_{yx}=1.02\text{Kg/cm.}$$

That means that, according to the regression line of weight on height, the weight will increase $1.02$ Kg for every cm that the height increases.

Regression predictions

Usually the regression models are used to predict the dependent variable for some values of the independent variable.

Example. In the sample of heights and weights, to predict the weight of a person with a height of 180 cm, we have to use the regression line of weight on height,

$$y=-108.49+1.02\cdot 180=75.11\text{ Kg}.$$

But to predict the height of a person with a weight of 79 Kg, we have to use the regression line of height on weight,

$$x=130.78+0.63\cdot 79=180.55\text{ cm}.$$

However, how reliable are these predictions?

Correlation

Once we have a regression model, in order to see if it is a good predictive model we have to assess the goodness of fit of the model and the strength of the of relation set by it. The part of Statistics in charge of this is correlation.

The correlation study the residuals of a regression model: the smaller the residuals, the greater the goodness of fit, and the stronger the relation set by the model.

Residual variance

To measure the goodness of fit of a regression model is common to use the residual variance.

Explained and non-explained variation

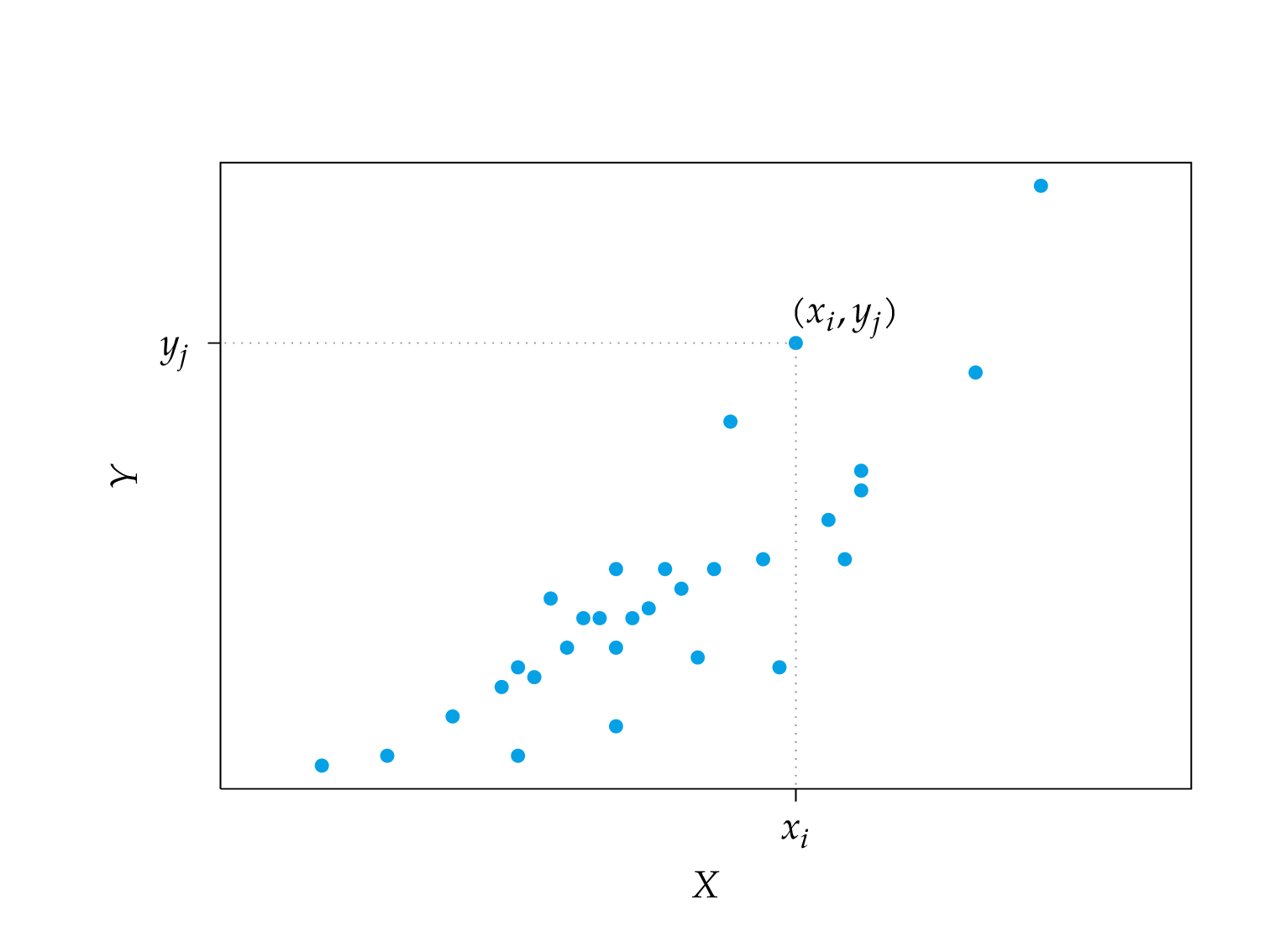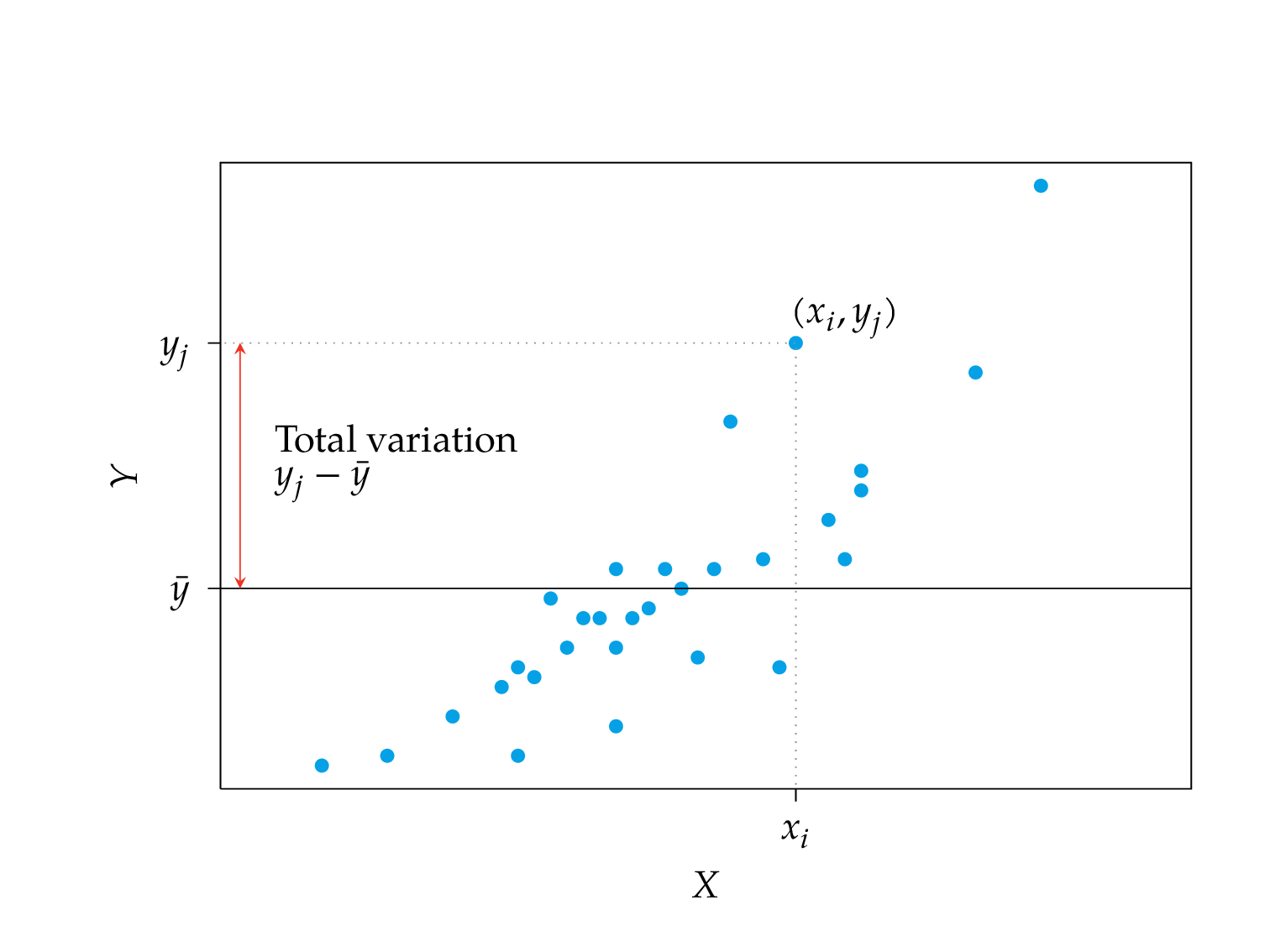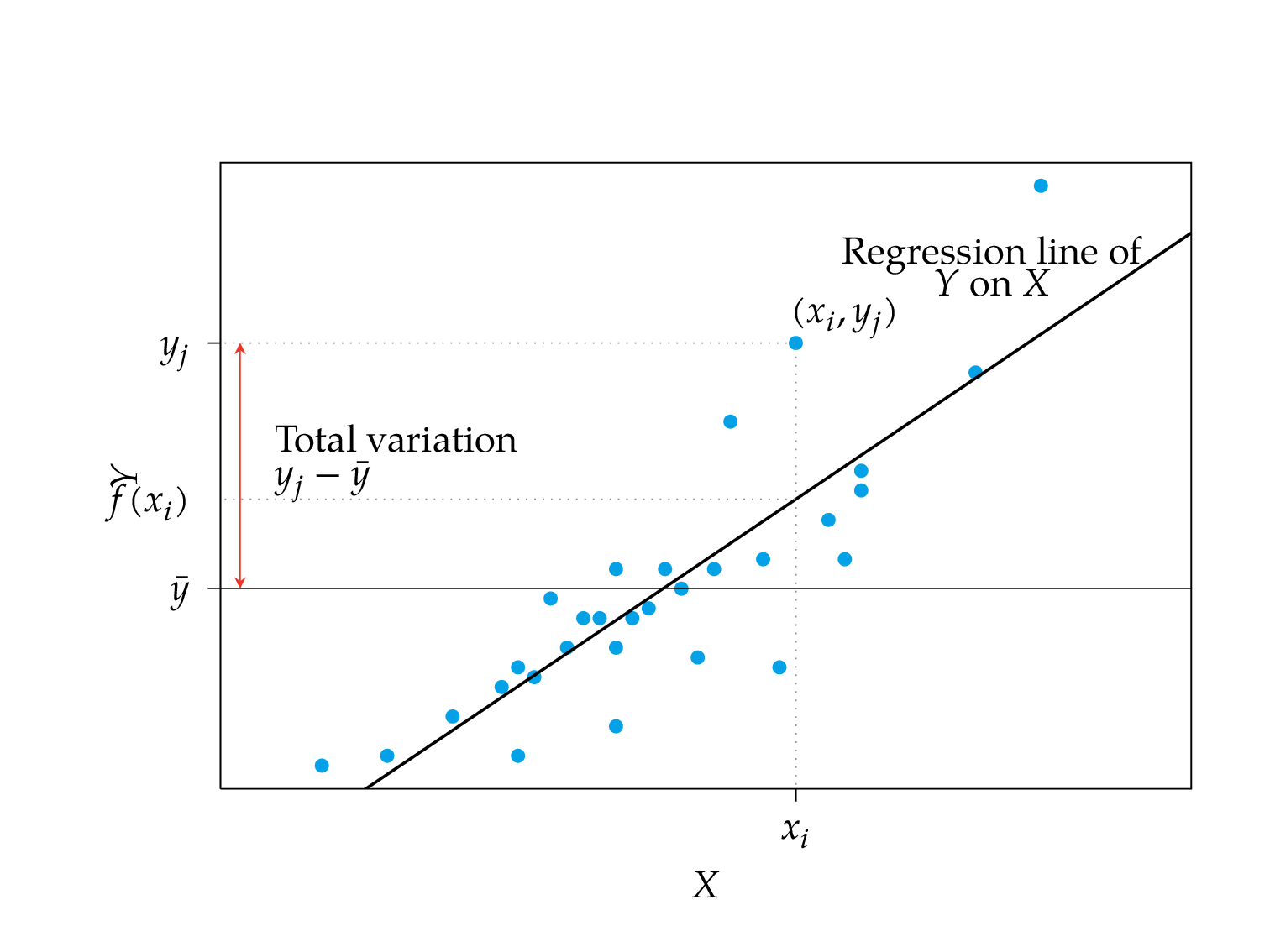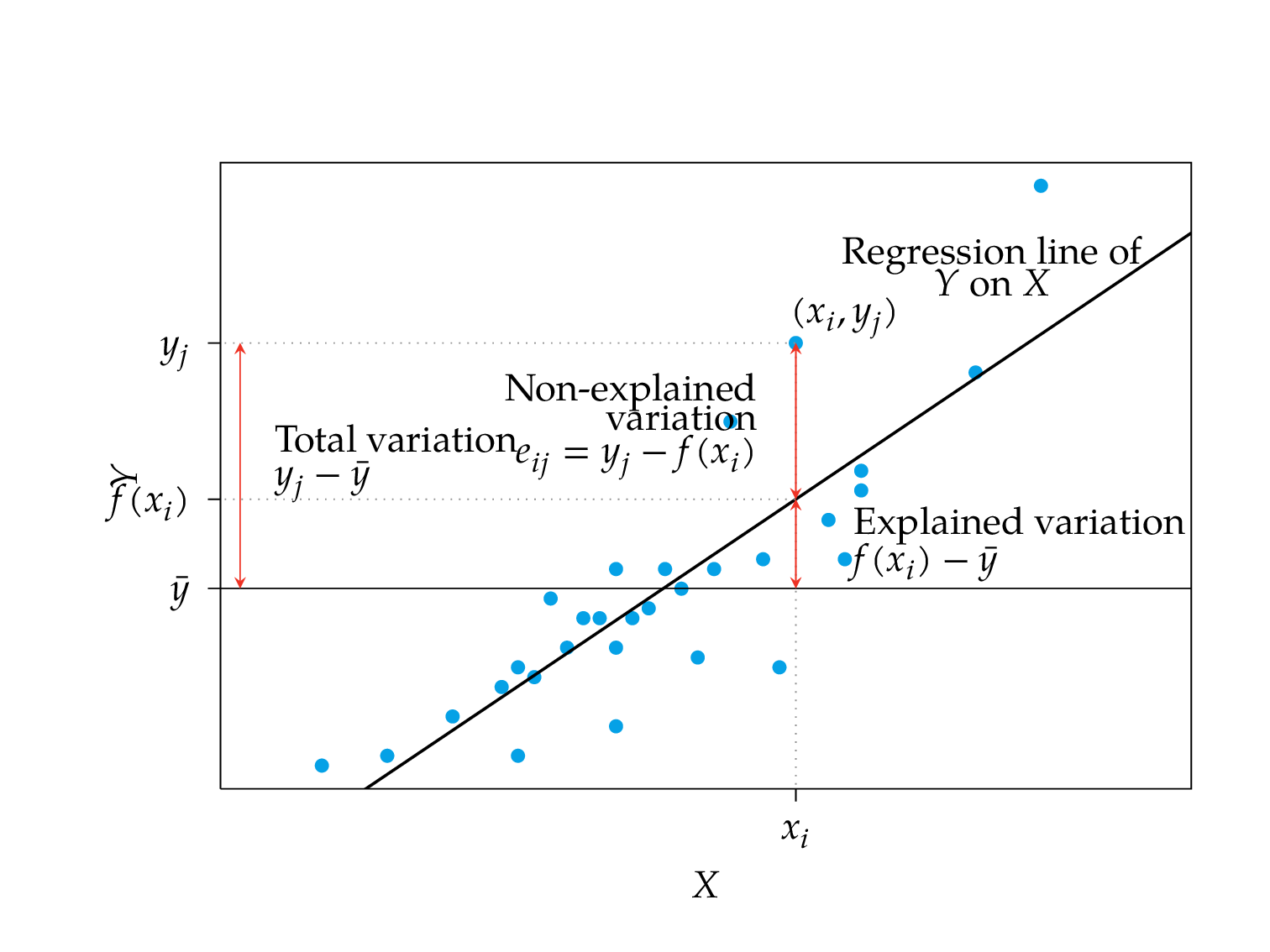
Coefficient of determination

From the residual variance is possible to define another correlation statistic easier to interpret.

Example. In the sample of heights and weights, we had

$$\begin{array}{lll}\overline{x}=174.67\text{ cm}& & s_x^2=102.06{\text{ cm}}^2\\ \overline{y}=69.67\text{ Kg}& & s_y^2=164.42{\text{ Kg}}^2\\ s_{xy}=104.07\text{ cm}\cdot \text{ Kg}\end{array}$$

Thus, the linear coefficient of determination is

$$r^2=\frac{s_{xy}^2}{s_x^2{s}_y^2}=\frac{(104.07\text{ cmcdot Kg}{)}^2}{102.06{\text{ cm}}^2\cdot 164.42{\text{ Kg}}^2}=0.65.$$

This means that the linear model of weight on height explains the 65% of the variation of weight, and the linear model of height on weight also explains 65% of the variation of height.

Correlation coefficient

Example. In the sample of heights and weights, we had

$$\begin{array}{lll}\overline{x}=174.67\text{ cm}& & s_x^2=102.06{\text{ cm}}^2\\ \overline{y}=69.67\text{ Kg}& & s_y^2=164.42{\text{ Kg}}^2\\ s_{xy}=104.07\text{ cm}\cdot \text{ Kg}\end{array}$$

Thus, the correlation coefficient is

$$r=\frac{s_{xy}}{s_x{s}_y}=\frac{104.07\text{ cmcdot Kg}}{10.1\text{ cm}\cdot 12.82\text{ Kg}}=+0.8.$$

This means that there is a rather strong linear, increasing, relation between height and weight.

Different linear correlations

The scatter plots below show linear regression models with differents correlations.

Reliability of regression predictions

The coefficient of determination explains the goodness of fit of a regression model, but there are other factors that influence the reliability of regression predictions:

• The coefficient of determination: The greater $r^2$, the greater the goodness of fit and the more reliable the predictions are.

• The variability of the population distribution: The greater the variation, the more difficult to predict and the less reliable the predictions are.

• The sample size: The greater the sample size, the more information we have and the more reliable the predictions are.

Non-linear regression

The fit of a non-linear regression can be also done by the least square fitting method.

However, in some cases the fitting of a non-linear model can be reduced to the fitting of a linear model applying a simple transformation to the variables of the model.

Transformations of non-linear regression models

• Logarithmic: A logarithmic model $y=a+b\log x$ can be transformed in a linear model with the change $t=\log x$:

  $$y=a+b\log x=a+bt.$$

• Exponential: An exponential model $y=e^{a+bx}$ can be transformed in a linear model with the change $z=\log y$:

  $$z=\log y=\log (e^{a+bx})=a+bx.$$

• Potential: A potential model $y=a{x}^b$ can be transformed in a linear model with the changes $t=\log x$ and $z=\log y$:

  $$z=\log y=\log (a{x}^b)=\log a+b\log x=a^{\prime }+bt.$$

• Inverse: An inverse model $y=a+b/x$ can be transformed in a linear model with the change $t=1/x$:

  $$y=a+b(1/x)=a+bt.$$

• Sigmoidal: A sigmoidal model $y=e^{a+b/x}$ can be transformed in a linear model with the changes $t=1/x$ and $z=\log y$:

  $$z=\log y=\log (e^{a+b/x})=a+b(1/x)=a+bt.$$

Exponential relation

Example. The number of bacteria in a culture evolves with time according to the table below.

$$\begin{array}{cc}\text{Hours}& \text{Bacteria}\\ 0& 25\\ 1& 28\\ 2& 47\\ 3& 65\\ 4& 86\\ 5& 121\\ 6& 190\\ 7& 290\\ 8& 362\end{array}$$

The scatter plot of the sample is showed below.

Fitting a linear model we get

$$\text{Bacteria}=-30.18+41,27,\text{Hours, with }{r}^2=0.85.$$

Is a good model?

Although the linear model is not bad, according to the shape of the point cloud of the scatter plot, an exponential model looks more suitable.

To construct an exponential model $y=e^{a+bx}$ we can apply the transformation $z=\log y$, that is, applying a logarithmic transformation to the dependent variable.

$$\begin{array}{ccc}\text{Hours}& \text{Bacteria}& \log \text{(Bacteria)}\\ 0& 25& 3.22\\ 1& 28& 3.33\\ 2& 47& 3.85\\ 3& 65& 4.17\\ 4& 86& 4.45\\ 5& 121& 4.80\\ 6& 190& 5.25\\ 7& 290& 5.67\\ 8& 362& 5.89\end{array}$$

Now it only remains to compute the regression line of the logarithm of bacteria on hours,

$$\log \text{(Bacteria)}=3.107+0.352,\text{Horas},$$

and, undoing the change of variable,

$$\text{Bacteria}=e^{3.107+0.352,\text{Hours}},\text{ with }{r}^2=0.99.$$

Thus, the exponential model fits much better than the linear model.

Regression risks

Lack of fit does not mean independence

It is important to note that every regression model has its own coefficient of determination.

Outliers influence in regression

Outliers in regression studies are points that clearly do not follow the tendency of the rest of points, even if the values of the pair are not outliers for every variable separately.

Outliers in regression studies can provoke drastic changes in the regression models.

The Simpson’s paradox

Sometimes a trend can disappears or even reverses when we split the sample into groups according to a qualitative variable that is related to the dependent variable. This is known as the Simpson’s paradox.

Example. The scatterplot below shows an inverse relation between the study hours and the score in an exam.

But if we split the sample in two groups (good and bad students) we get different trends and now the relation is direct, which makes more sense.