8  Análisis Estadísticos

El tipo de estudio estadístico más apropiado en cada caso depende de varios factores:

• El objetivo del estudio.
• El número de variables que intervienen.
• El tipo de las variables dependientes e independientes.
• La naturaleza de las observaciones (independientes o emparejadas).

A continuación se presentan los estudios estadísticos más habituales en función de estos factores. La siguiente tabla de resumen de contrastes de hipótesis más habituales puede ayudar a identificar el más apropiado en cada caso.

Variables independientes	Variable dependiente	Objetivo	Ejemplo	Contraste
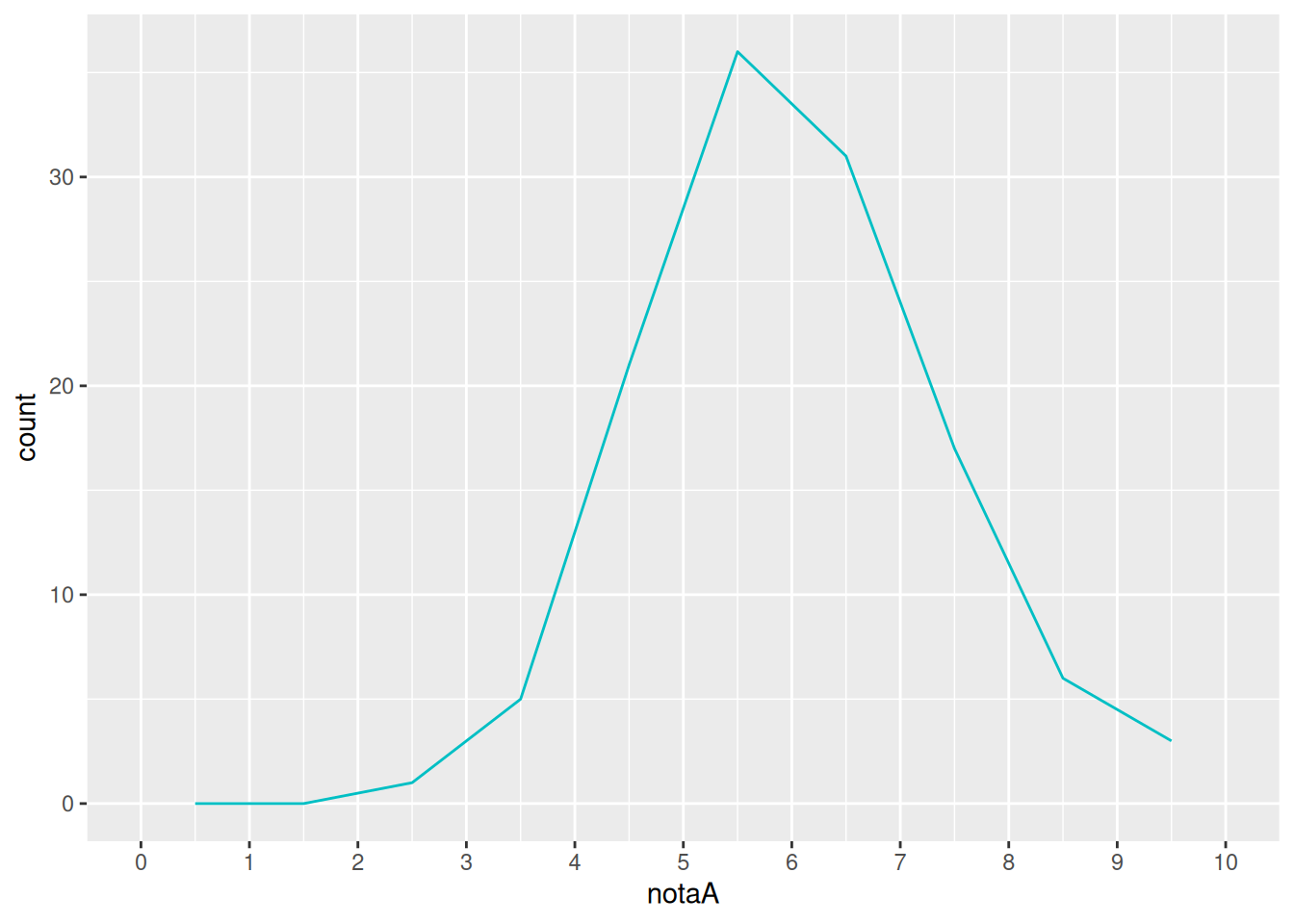
Ninguna (Una población)	Cuantitativa	Contrastar la normalidad de una variable	Comprobar si la nota de un examen tiene distribución normal (forma de campana de Gauss)	Komogorov-Smirnov (requiere muestras grandes)
				Shapiro-Willks
	Cuantitativa normal	Contrastar si la media poblacional de una variable tiene un valor determinado	Comprobar si la nota media de un examen es 5	Test T para la media de una población
	Cuantitativa o cualitativa ordinal	Contrastar si la mediana poblacional de una variable tiene un valor determinado	Comprobar si la calificación mediana de un examen es Aprobado	Test para la mediana de una población
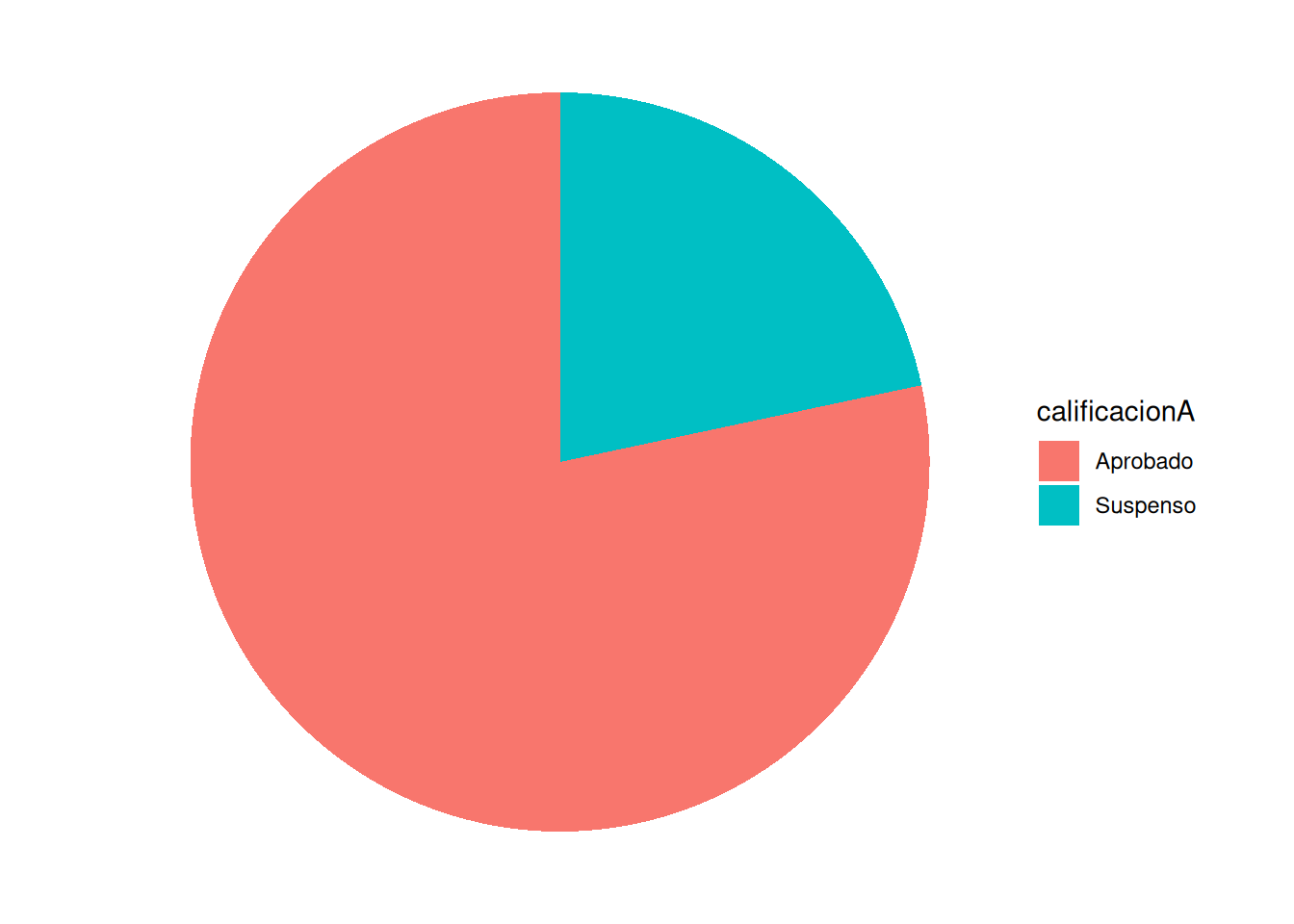
	Cualitativa (2 categorías)	Contrastar si la proporción poblacional de una de las categorías tiene un valor determinado	Comprobar si la proporción de aprobados es de la mitad (o que el porcentaje es 50%)	Test Binomial
	Cualitativa	Contrastar si las proporciones de cada una de las categorías tienen un valor determinado	Comprobar si las proporciones de alumnos matriculados en ciencias, letras o mixtas son 0.5, 0.2 y 0.3 respectivamente	Test Chi-cuadrado de bondad de ajuste
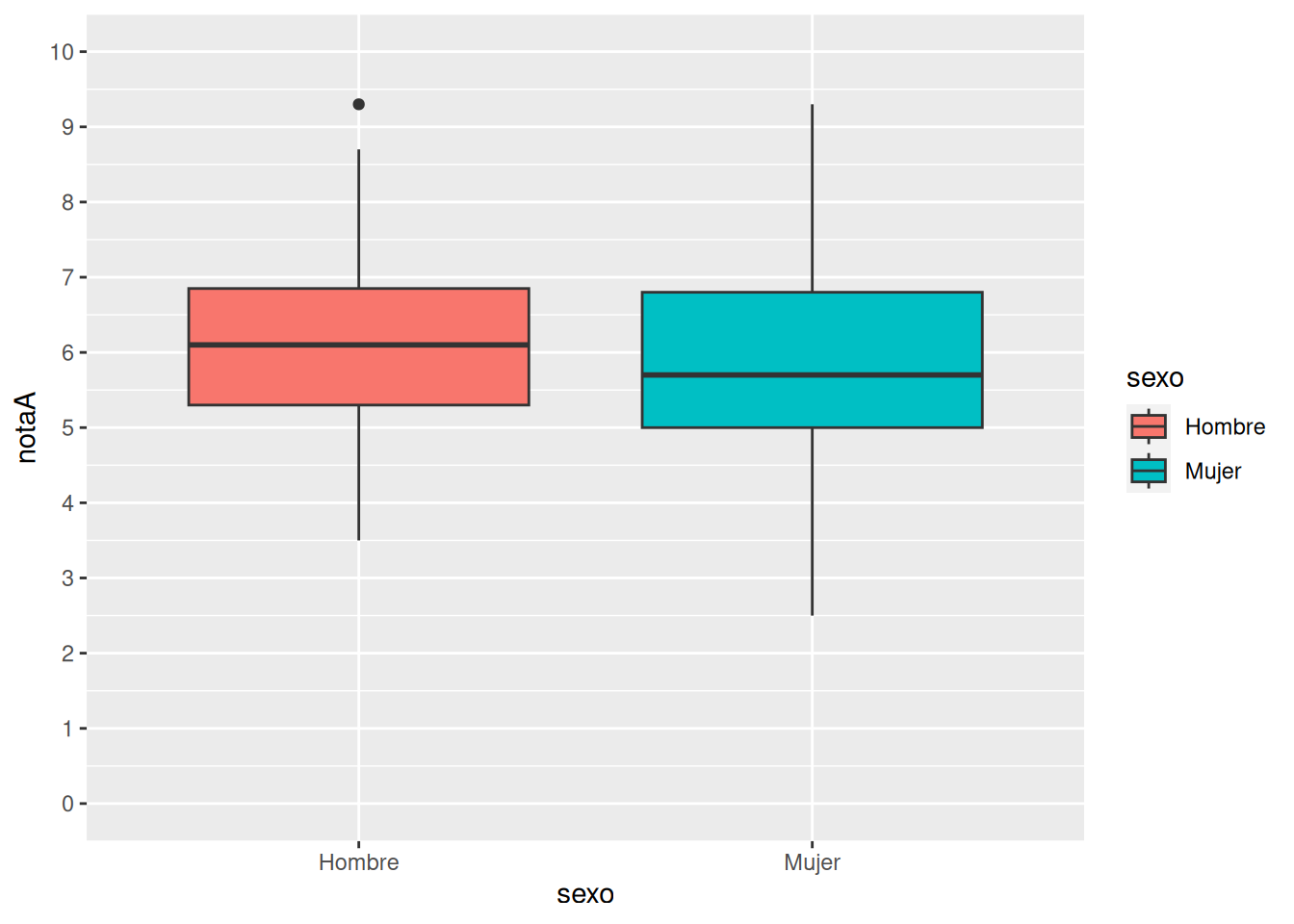
Una cualitativa con dos categorías independientes (Dos poblaciones independientes)	Cuantitativa normal	Contrastar si hay diferencias entre las medias la variable dependiente en dos poblaciones independientes	Comprobar si el grupo de mañana y el grupo de tarde han tenido notas medias diferentes	Test T para la comparación de medias de poblaciones independientes
		Contrastar si hay diferencias entre las varianzas de la variable dependiente en dos poblaciones independientes	Comprobar si hay diferencias entre la variabilidad de las notas del grupo de mañana y el de tarde	Test F de Fisher
		Contrastar si hay concordancia o acuerdo entre las dos variables	Comprobar si hay concordancia o acuerdo entre las notas que ponen dos profesores distintos para los mismos exámenes	Correlación intraclase
	Cuantitativa o cualitativa ordinal	Contrastar si hay diferencias entre las distribuciones de la variable dependiente en dos poblaciones independientes	Comprobar si el grupo de mañana y el grupo de tarde han tenido calificaciones diferentes	Test de la U de Mann-Whitney
		Contrastar si hay concordancia o acuerdo entre las dos variables	Comprobar si hay concordancia o acuerdo entre las calificaciones que ponen dos profesores distintos para los mismos exámenes	Kappa de Cohen
	Cualitativa	Contrastar si hay relación entre las dos variables o bien si hay diferencias entre las proporciones de las categorías de la variable dependiente en las dos poblaciones definidas por las categorías de la variable independiente	Comprobar si existe relación entre los aprobados en una asignatura y el grupo al que pertenecen los alumnos, es decir, si la proporción de aprobados es diferente en dos grupos distintos.	Test Chi-cuadrado (si no ha más del 20% de frecuencias esperadas menores que 5) Test exacto de Fisher
		Contrastar si hay concordancia o acuerdo entre las dos variables	Comprobar si hay concordancia o acuerdo entre la valoración (aprobado o suspenso) que hacen dos profesores distintos para los mismos exámenes	Kappa de Cohen
Una cualitativa con dos categorías relacionadas o pareadas (Dos poblaciones relacionadas o pareadas)	Cuantitativa normal	Contrastar si hay diferencias entre las medias de la variable dependiente en dos poblaciones relacionadas o pareadas	Comprobar si las notas medias de dos asignaturas cursadas por los mismos alumnos han sido diferentes o si las notas medias de un examen realizado al comienzo del curso (antes) y otro al final (después) de una misma asignatura han sido diferentes	Test T para la comparación de medias de poblaciones relacionadas o pareadas
	Cuantitativa o cualitativa ordinal	Contrastar si hay diferencias entre las distribuciones de la variable dependiente en dos poblaciones relacionadas o pareadas	Comprobar si las calificaciones de dos asignaturas cursadas por los mismos alumnos han sido diferentes	Test de Wilcoxon
	Cualitativa con dos categorías	Contrastar si hay diferencias entre las proporciones de las categorías de la variable dependiente en dos poblaciones relacionadas o pareadas	Comprobar si la proporción o el porcentaje de aprobados en un examen es distinta al comienzo y al final del curso	Test de McNemar
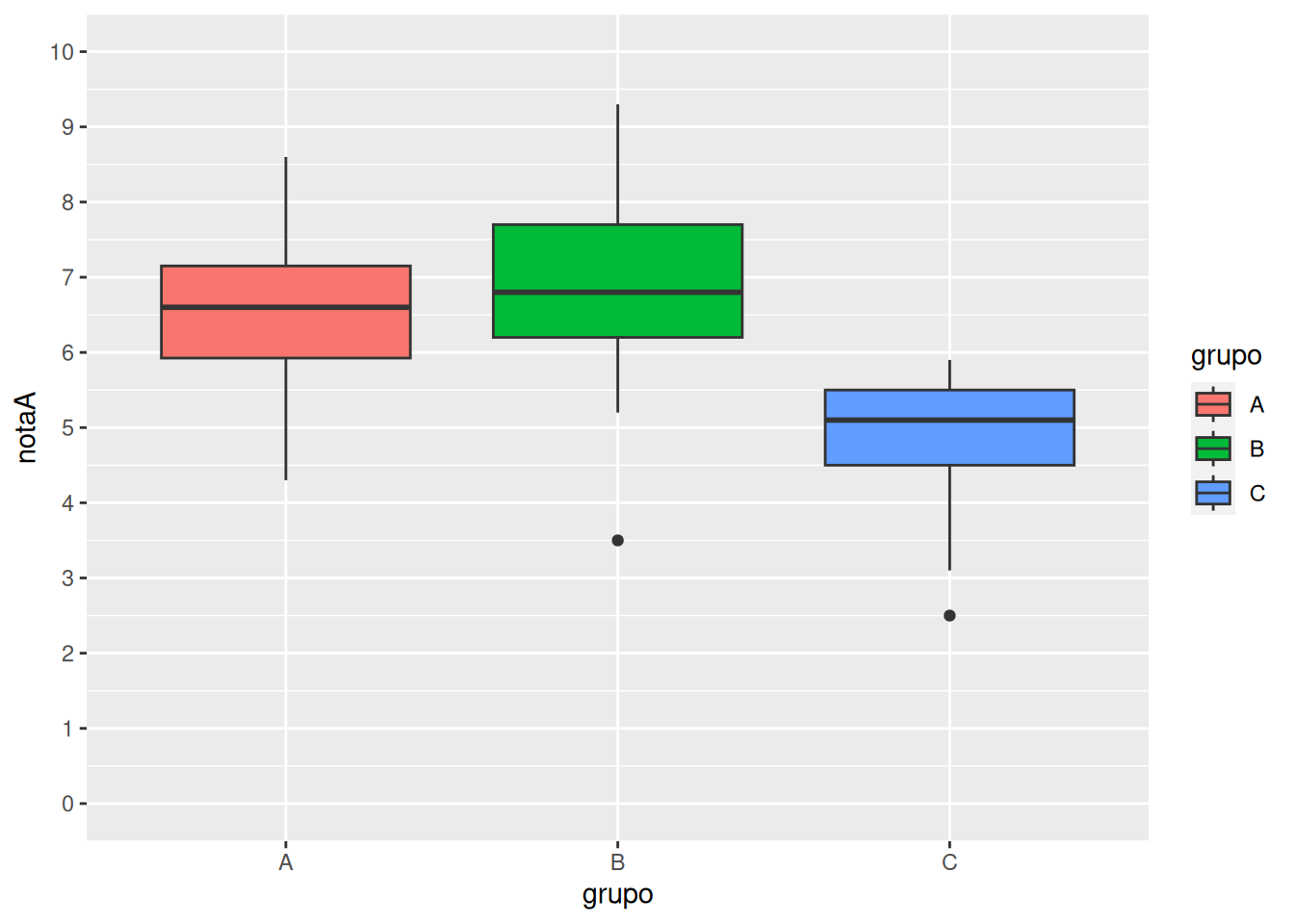
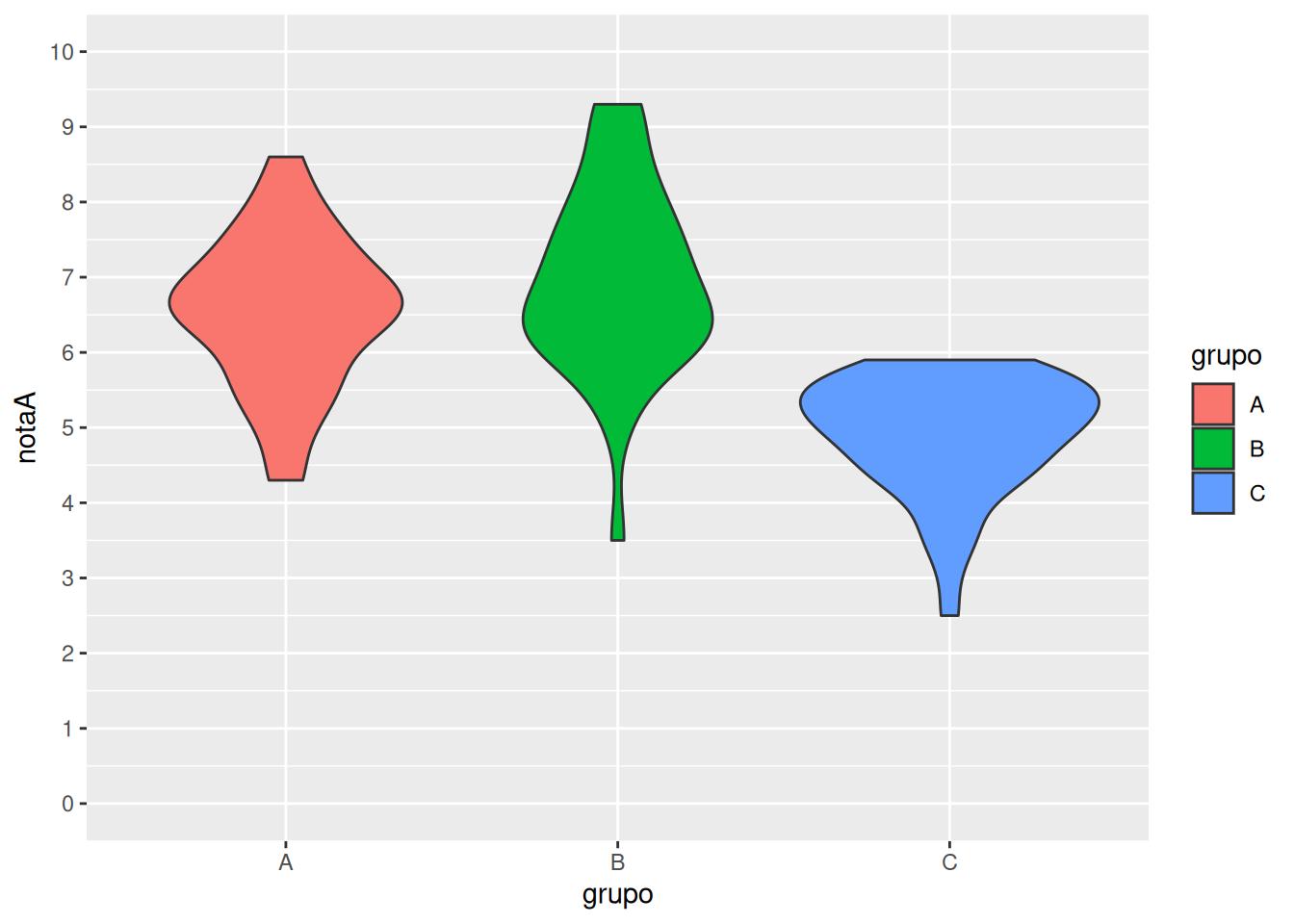
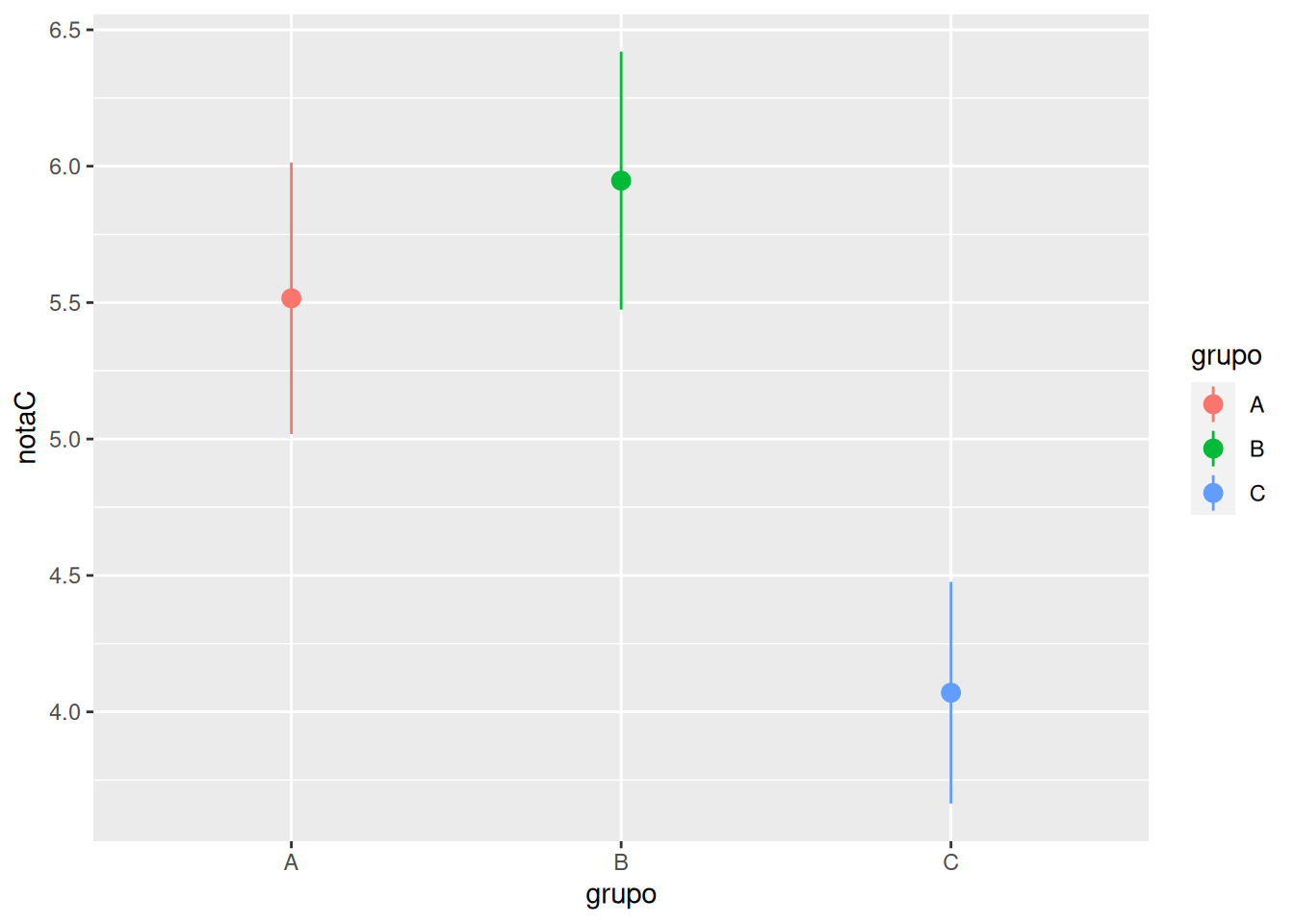
Una cualitativa con dos o más categorías independientes (Dos o más poblaciones independientes)	Cuantitativa normal y homogeneidad de varianzas	Contrastar si hay diferencias entre las medias la variable dependiente en cada una de las poblaciones definidas por las categorías de la variable independiente	Comprobar si existen diferencias entre las notas medias de tres grupos distintos de clase.	Análisis de la Varianza de un factor (ANOVA) Si hay diferencias > Test de Tukey o Bonferroni para la diferencia por pares
	Cuantitativa normal	Contrastar si hay diferencias entre las varianzas de la variable dependiente en cada una de las poblaciones definidas por las categorías de la variable independiente	Comprobar si la variabilidad de las notas de una asignatura es distinta en tres grupos diferentes de clase	Prueba de Levene para la homogeneidad de varianzas
	Cuantitativa o cualitativa ordinal	Contrastar si hay diferencias entre las distribuciones de la variable dependiente en cada una de las poblaciones definidas por las categorías de la variable independiente	Comprobar si existen diferencias entre las calificaciones de tres grupos distintos de clase	Test de Kruskal Wallis
	Cualitativa	Contrastar si hay relación entre las dos variables o bien si hay diferencias entre las proporciones de las categorías de la variable dependiente en cada una de las poblaciones definidas por las categorías de la variable independiente	Comprobar si existe relación entre los aprobados en una asignatura y el grupo al que pertenecen los alumnos, es decir, si la proporción de aprobados es diferente en los distintos grupos.	Test Chi-cuadrado (si no ha más del 20% de frecuencias esperadas menores que 5) Test exacto de Fisher
Una cualitativa con dos o más categorías relacionadas (medidas repetidas)	Cuantitativa normal	Contrastar si hay diferencias entre las medias repetidas de la variable dependiente	Comprobar si hay diferencias entre las notas que otorgan varios profesores a un mismo examen	Análisis de la Varianza (ANOVA) de medidas repetidas de un factor
	Cuantitativa o cualitativa ordinal	Contrastar si hay diferencias entre las medidas repetidas de la variable dependiente	Comprobar si hay diferencias entre las calificaciones que otorgan varios profesores a un mismo examen	Test de Friedman
	Cualitativa	Contrastar si hay diferencias entre las valoraciones repetidas de la variable dependiente	Comprobar si hay diferencias entre la valoración (aprobado o suspenso) que hacen varios profesores de un mismo examen	Regresión logística de medidas repetidas
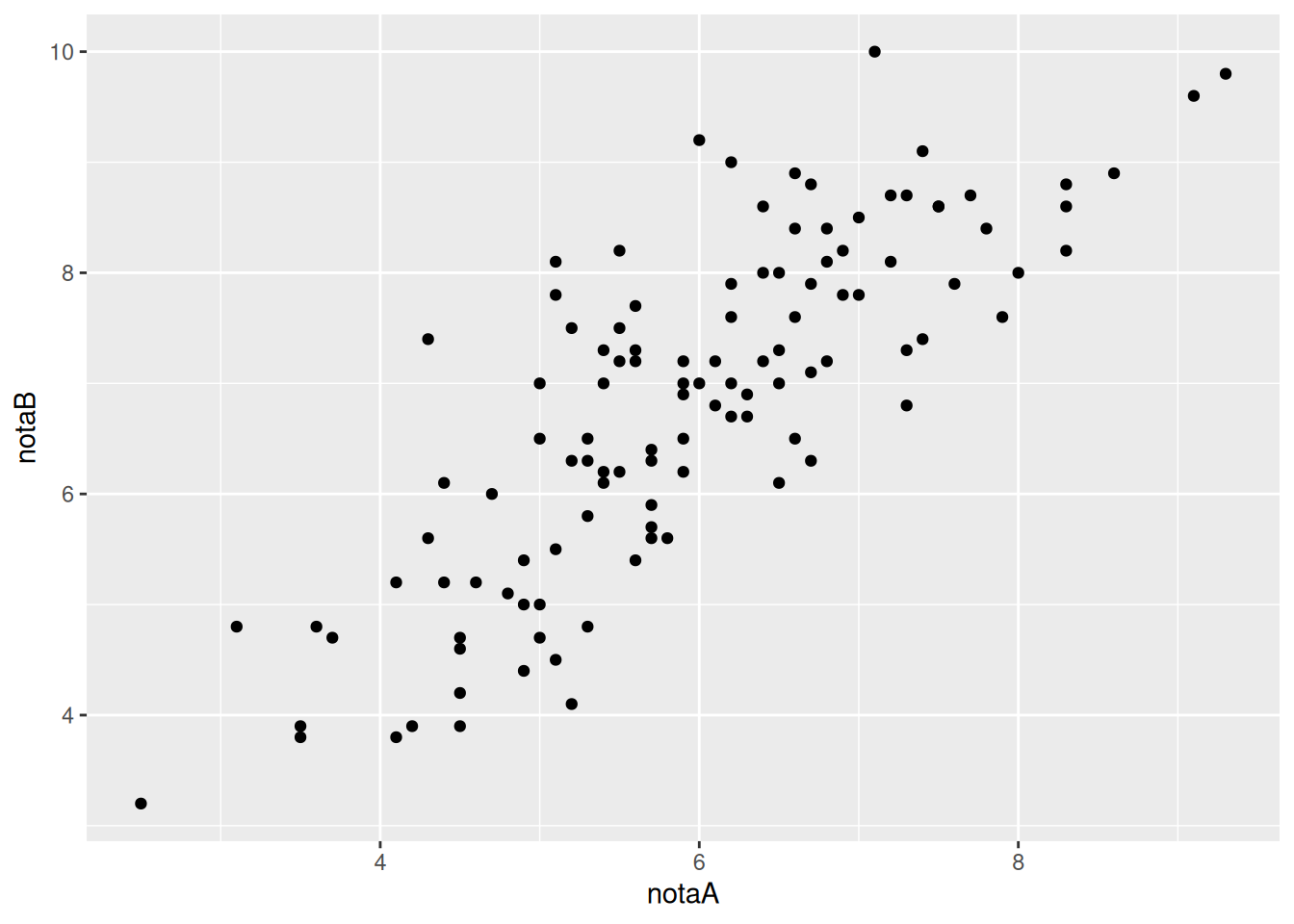
Una cuantitativa normal	Cuantitativa normal	Contrastar si existe relación lineal entre las dos variables	Comprobar si existe relación entre las notas de dos asignaturas	Correlación de Pearson
		Construir un modelo predictivo que explique la variable dependiente en función de la independiente	Construir el modelo (función de regresión) que mejor explique la relación entre la nota de un examen y las horas dedicadas a su estudio	Regresión simple (lineal o no lineal)
	Cuantitativa o cualitativa ordinal	Contrastar si existe relación lineal entre las dos variables	Comprobar si existe relación entre las calificaciones de dos asignaturas	Correlación de Spearman
	Cualitativa	Construir un modelo predictivo que explique la variable dependiente en función de la independiente	Construir el modelo (función logística) que mejor explique la relación entre el resultado de un examen (aprobado o suspenso) y las horas dedicadas a su estudio	Regresión logística simple

Los ejemplos de los distintos test que se presentan a continuación se han realizado a partir del siguiente conjunto de datos que contiene las notas y calificaciones de un curso. El fichero con los datos puede descargarse aquí para reproducir los estudios: notas-curso.csv.

library(tidyverse)
df <- read.csv('https://raw.githubusercontent.com/asalber/manual-r/master/datos/notas-curso.csv')
head(df)

    sexo  turno grupo trabaja notaA notaB notaC notaD notaE calificacionA
1  Mujer  Tarde     C       N   5.2   6.3   3.4   2.3   2.0      Aprobado
2 Hombre Mañana     A       N   5.7   5.7   4.2   3.5   2.7      Aprobado
3 Hombre Mañana     B       N   8.3   8.8   8.8   8.0   5.5      Aprobado
4 Hombre Mañana     B       N   6.1   6.8   4.0   3.5   2.2      Aprobado
5 Hombre Mañana     A       N   6.2   9.0   5.0   4.4   3.7      Aprobado
6 Hombre Mañana     A       S   8.6   8.9   9.5   8.4   3.9      Aprobado
  calificacionB calificacionC calificacionD calificacionE asinaturas.aprobadas
1      Aprobado      Suspenso      Suspenso      Suspenso                    2
2      Aprobado      Suspenso      Suspenso      Suspenso                    2
3      Aprobado      Aprobado      Aprobado      Aprobado                    5
4      Aprobado      Suspenso      Suspenso      Suspenso                    2
5      Aprobado      Aprobado      Suspenso      Suspenso                    3
6      Aprobado      Aprobado      Aprobado      Suspenso                    4
  nota.media
1        3.8
2        4.3
3        7.9
4        4.5
5        5.7
6        7.8

8.1 Una variable cuantitativa

8.1.1 Estudios descriptivos

8.1.1.1 Estadísticos

• Tamaño muestral
• Media
• Desviación típica
• Mínimo, Máximo
• Cuartiles
• Coeficiente de asimetría
• Coeficiente de apuntamiento

# Tamaño muestral
nrow(df)

[1] 120

# Media
mean(df$notaA, na.rm = TRUE)

[1] 6.028333

# Desviación típica
sd(df$notaA, na.rm = TRUE)

[1] 1.340524

# Min, max
min(df$notaA, na.rm = TRUE)

[1] 2.5

max(df$notaA, na.rm = TRUE)

[1] 9.3

# Cuartiles
quantile(df$notaA, c(0.25, 0.5, 0.75), na.rm = TRUE)

  25%   50%   75% 
5.100 5.900 6.825 

# Coef. asimetría
library(moments)
skewness(df$notaA, na.rm = TRUE)

[1] 0.1373915

# Coef. apuntamiento
kurtosis(df$notaA, na.rm = TRUE) - 3

[1] -0.102287

8.1.1.2 Gráficos

• Diagrama de barras (variables discretas)

df %>% ggplot(aes(x = asinaturas.aprobadas)) + 
  geom_bar(fill="#00BFC4") + 
  # Cambio de escala del eje X
  scale_x_discrete(limits=0:5) 

• Histograma

library(ggplot2)
# Límites de los intervalos
breaks = 0:10
# Histograma de las notasA
df %>% ggplot(aes(x = notaA)) + 
  geom_histogram(breaks = breaks, fill="#00BFC4") + 
  # Cambio de escala del eje X
  scale_x_continuous(limits=c(0, 10), breaks = 0:10) 

# Histograma de notasE
df %>% ggplot(aes(x = notaE)) + 
  geom_histogram(breaks = breaks, fill="#00BFC4") + 
  # Cambio de escala del eje X
  scale_x_continuous(limits=c(0, 10), breaks = 0:10) 

• Diagrama de líneas

# Variables discretas
df %>% count(asinaturas.aprobadas) %>%
  ggplot(aes(x = asinaturas.aprobadas, y = n)) +
  geom_line(col="#00BFC4") + 
  # Cambio de escala del eje X
  scale_x_discrete(limits=0:5) 

# Agrupación de datos en intervalos
df %>% ggplot(aes(x = notaA)) + 
  geom_freqpoly(breaks = breaks, col="#00BFC4") + 
  # Cambio de escala del eje X
  scale_x_continuous(limits=c(0, 10), breaks = 0:10) 

• Diagrama de caja y bigotes

df %>% ggplot(aes(x = notaA)) + 
  geom_boxplot(fill="#00BFC4") +
  # Cambio de escala del eje X
  scale_x_continuous(limits=c(0, 10), breaks = 0:10)

8.1.2 Estudios inferenciales

8.1.2.1 Test de normalidad de Shapiro-Wilk

Objetivo: Comprobar la normalidad de la distribución.

Hipótesis nula: La distribución es normal.

shapiro.test(df$notaA)

    Shapiro-Wilk normality test

data:  df$notaA
W = 0.99424, p-value = 0.907

shapiro.test(df$notaE)

    Shapiro-Wilk normality test

data:  df$notaE
W = 0.92264, p-value = 4.065e-06

8.1.2.2 Test t para la media de una población

Objetivo: Estimar la media de una variable o compararla con un valor dado μ₀.

Requisitos:

• Una variable cuantitativa.
• Distribución normal o tamaño muestral ≥ 30.

Hipótesis nula: La media de la población es igual a μ₀.

Ejemplo: Comprobar si la nota media de un examen es diferente de 5.

t.test(df$notaA, mu = 5, alternative = "two.sided")

    One Sample t-test

data:  df$notaA
t = 8.4033, df = 119, p-value = 1.08e-13
alternative hypothesis: true mean is not equal to 5
95 percent confidence interval:
 5.786023 6.270643
sample estimates:
mean of x 
 6.028333 

8.2 Una variable cualitativa

8.2.1 Estudios descriptivos

8.2.1.1 Estadísticos

• Tamaños muestral
• Frecuencias muestrales
• Proporciones/porcentajes muestrales

# Tamaño muestral sin datos perdidos
length(na.omit(df$calificacionB))

[1] 115

# Frecuencias
table(df$calificacionB)

Aprobado Suspenso 
      98       17 

# Proporciones
table(df$calificacionB) / length(na.omit(df$calificacionB))

 Aprobado  Suspenso 
0.8521739 0.1478261 

# Porcentajes
table(df$calificacionB) / length(na.omit(df$calificacionB)) * 100

Aprobado Suspenso 
85.21739 14.78261 

8.2.1.2 Gráficos

• Diagrama de sectores

df %>% ggplot(aes(x = "", fill = calificacionA)) + 
  geom_bar() +
  # Cambiar a coordenadas polares
  coord_polar(theta = "y") +
  # Eliminar ejes
   theme_void()

8.2.2 Estudios inferenciales

8.2.2.1 Test binomial para una proporción de una población

Objetivo: Estimar la propoción de una categoría en una población o compararla con un valor p₀.

Requisitos:

• One variable cualitativa

Hipótesis nula: La proporción poblacional es igual a p₀.

Ejemplo: Comprobar si la proporción de aprobados es mayor de 0.5.

n <- nrow(df)
freq <- table(df$calificacionA)["Aprobado"]
binom.test(freq, n, p = 0.5, alternative = "greater")

    Exact binomial test

data:  freq and n
number of successes = 94, number of trials = 120, p-value = 1.57e-10
alternative hypothesis: true probability of success is greater than 0.5
95 percent confidence interval:
 0.7123183 1.0000000
sample estimates:
probability of success 
             0.7833333 

8.2.2.2 Test Z para la proporción de una población

Objetivo: Estimar la propoción de una categoría en una población o compararla con un valor p₀.

Requisitos:

• Una variable cualitativa
• Tamaño muestral >= 30

Observación: Utiliza la aproximación normal de la distribución Binomal.

Ejemplo: Comprobar si la proporción de aprobados es mayor de 0.5.

freq <- table(df$calificacionA)["Aprobado"]
prop.test(freq, n, p = 0.7, alternative = "greater")

    1-sample proportions test with continuity correction

data:  freq out of n, null probability 0.7
X-squared = 3.5813, df = 1, p-value = 0.02922
alternative hypothesis: true p is greater than 0.7
95 percent confidence interval:
 0.7111099 1.0000000
sample estimates:
        p 
0.7833333 

8.3 Dos variables: Variable dependiente cuantitativa y variable independiente culitativa con dos categorías o grupos

8.3.1 Estudios descriptivos

8.3.1.1 Estadísticos

• Tamaño muestral de cada grupo
• Media de cada grupo
• Desviación típica de cada grupo
• Mínimo, Máximo de cada grupo
• Cuartiles de cada grupo
• Coeficiente de asimetría de cada grupo
• Coeficiente de apuntamiento de cada grupo

# Tamaño muestral de notaA según el sexo
df %>% group_by(sexo) %>% group_size()

[1] 71 49

# Media, Desviación típica, Mín, Máx, Cuartiles, Coef. Asimetría y Coef. Apuntamiento
library(moments)
df %>% group_by(sexo) %>% summarize(Media = mean(notaA, na.rm=TRUE), Des.Tip = sd(notaA, na.rm = TRUE), Mín = min(notaA), Máx = max(notaA), C1 = quantile(notaA, 0.25, na.rm = TRUE), C2 = quantile(notaA, 0.5, na.rm = TRUE), C3 = quantile(notaA, 0.75, na.rm = TRUE), Coef.Asimetría = skewness(notaA, na.rm = TRUE), Coef.Apuntamiento = kurtosis(notaA, na.rm = TRUE) - 3)

# A tibble: 2 × 10
  sexo   Media Des.Tip   Mín   Máx    C1    C2    C3 Coef.Asimetría Coef.Apunt…¹
  <chr>  <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>          <dbl>        <dbl>
1 Hombre  6.12    1.23   3.5   9.3   5.3   6.1  6.85          0.249       -0.170
2 Mujer   5.89    1.49   2.5   9.3   5     5.7  6.8           0.135       -0.240
# … with abbreviated variable name ¹​Coef.Apuntamiento

8.3.1.2 Gráficos

• Diagrama de cajas y bigotes

df %>% ggplot(aes(x = sexo, y = notaA, fill = sexo)) + 
  geom_boxplot() +
  # Cambio de escala del eje y
  scale_y_continuous(limits=c(0, 10), breaks = 0:10)

• Diagrama de violín

df %>% ggplot(aes(x = sexo, y = notaA, fill = sexo)) + 
  geom_violin() +
  # Cambio de escala del eje y
  scale_y_continuous(limits=c(0, 10), breaks = 0:10)

8.3.2 Estudios inferenciales

8.3.2.1 Test de normalidad de Shapiro-Wilks

Objetivo: Comprobar la normalidad de la distribución de cada población.

Hipótesis nula: La distribución es normal.

df %>% group_by(sexo) %>% 
  summarise(`Estadístico W` = shapiro.test(notaA)$statistic, `p-valor` = shapiro.test(notaA)$p.value)

# A tibble: 2 × 3
  sexo   `Estadístico W` `p-valor`
  <chr>            <dbl>     <dbl>
1 Hombre           0.990     0.872
2 Mujer            0.990     0.942

8.3.2.2 Test F de Fisher de comparación de varianzas de dos poblaciones independientes

Objetivo: Comparar las varianzas de dos poblaciones independientes.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con dos categorías (poblaciones)
• Distribución normal de la variable dependiente en ambas poblaciones o tamaños de las muestras de cada población ≥ 30.

Hipótesis nula: La varianzas poblacionales son iguales (no existe una diferencia significativa entre las medias poblacionales).

Ejemplo: Comprobar si diferencias signicativas entre las notas medias de hombres y mujeres.

# Test de comparación de varianzas
var.test(notaA ~ sexo, data = df)

    F test to compare two variances

data:  notaA by sexo
F = 0.6769, num df = 70, denom df = 48, p-value = 0.1347
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.3953421 1.1293155
sample estimates:
ratio of variances 
         0.6769032 

8.3.2.3 Test t de comparación de medias de dos poblaciones independientes

Objetivo: Estimar la diferencia de medias en las dos poblaciones o comprobar si hay diferencias significativas entre ellas.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con dos categorías (poblaciones)
• Distribución normal de la variable dependiente en ambas poblaciones o tamaños de las muestras de cada población ≥ 30.

Hipótesis nula: La medias poblacionales son iguales (no existe una diferencia significativa entre las medias poblacionales).

Observación: El resultado del test depende de si las varianzas poblacionales son iguales o no.

Ejemplo: Comprobar si diferencias signicativas entre las notas medias de hombres y mujeres.

# Test de comparación de varianzas
var.test(notaA ~ sexo, data = df)

    F test to compare two variances

data:  notaA by sexo
F = 0.6769, num df = 70, denom df = 48, p-value = 0.1347
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.3953421 1.1293155
sample estimates:
ratio of variances 
         0.6769032 

# Test de comparación de medias asumiendo varianzas iguales
t.test (notaA ~ sexo, data = df, alternative = "two.sided", var.equal = FALSE)

    Welch Two Sample t-test

data:  notaA by sexo
t = 0.89364, df = 89.873, p-value = 0.3739
alternative hypothesis: true difference in means between group Hombre and group Mujer is not equal to 0
95 percent confidence interval:
 -0.2821809  0.7435779
sample estimates:
mean in group Hombre  mean in group Mujer 
            6.122535             5.891837 

# Test de comparación de medias asumiendo varianzas iguales
t.test (notaA ~ sexo, data = df, alternative = "two.sided", var.equal = TRUE)

    Two Sample t-test

data:  notaA by sexo
t = 0.92608, df = 118, p-value = 0.3563
alternative hypothesis: true difference in means between group Hombre and group Mujer is not equal to 0
95 percent confidence interval:
 -0.262615  0.724012
sample estimates:
mean in group Hombre  mean in group Mujer 
            6.122535             5.891837 

• Diagrama de medias

df %>% ggplot(aes(x = sexo, y = notaA, colour = sexo)) + 
  # Puntos de medias
  stat_summary(fun="mean", size=3,  geom="point", position=position_dodge(width=0.25)) + 
  # Intervalos de confianza para la media
  stat_summary(fun.data = function(x) mean_cl_normal(x, conf.int=0.95), geom = "pointrange", position=position_dodge(width=0.25)) 

8.3.2.4 Test U de Mann-Whitney de comparación de dos poblaciones independientes (no paramétrico)

Objetivo: Comprobar si hay diferencias significativas entre entre dos poblaciones independientes.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con dos categorías (poblaciones)

Hipótesis nula: La medianas poblacionales son iguales (no existe una diferencia significativa entre las medianas poblacionales).

Ejemplo: Comprobar si diferencias signicativas entre las notas de hombres y mujeres.

# Test de rangos U the Mann-Whitney
wilcox.test(notaA ~ sexo, data = df, alternative = "two.sided")

    Wilcoxon rank sum test with continuity correction

data:  notaA by sexo
W = 1917, p-value = 0.3445
alternative hypothesis: true location shift is not equal to 0

8.4 Dos variables: Variable dependiente cuantitativa y variable independiente culitativa con dos categorías o grupos pareados

Dos grupos o poblaciones están pareadas o emparejadas cuando los dos poblaciones contienen los mismos individuos, es decir, se trata en realidadad de una única población, pero la variable dependiente se mide dos veces en cada individuo (normalmente antes y después de la algún suceso) y por tanto cada individuo tiene asociado un par de valores.

Este estudio puede realizarse también creando una nueva variable a partir de la resta de las dos mediciones y planteando un estudio de una sola variable cuantitativa.

Ejemplo: Creación de la diferencia de notas de las asignaturas A y B.

# Creamos la variable diferencia = notaA - notaB
df <- df %>% mutate(diferencia = notaA - notaB)

8.4.1 Estudios descriptivos

8.4.1.1 Estadísticos

• Tamaño muestral del grupo
• Media de la diferencia
• Desviación típica de la diferencia
• Mínimo, Máximo de la diferencia
• Cuartiles de la diferencia
• Coeficiente de asimetría de la diferencia
• Coeficiente de apuntamiento de la diferencia

Ejemplo: Estadísticos descriptivos de la diferencia entre las notas de las asignaturas A y B de un mismo grupo de alumnos.

# Tamaño muestral de sin contar los datos perdidos
length(na.omit(df$diferencia))

[1] 115

# Media, Desviación típica, Mín, Máx, Cuartiles, Coef. Asimetría y Coef. Apuntamiento
library(moments)
df %>% summarize(Media = mean(diferencia, na.rm=TRUE), Des.Tip = sd(diferencia, na.rm = TRUE), Mín = min(diferencia, na.rm = TRUE), Máx = max(diferencia, na.rm = TRUE), C1 = quantile(diferencia, 0.25, na.rm = TRUE), C2 = quantile(diferencia, 0.5, na.rm = TRUE), C3 = quantile(diferencia, 0.75, na.rm = TRUE), Coef.Asimetría = skewness(diferencia, na.rm = TRUE), Coef.Apuntamiento = kurtosis(diferencia, na.rm = TRUE) - 3)

       Media   Des.Tip  Mín Máx   C1   C2   C3 Coef.Asimetría Coef.Apuntamiento
1 -0.8817391 0.9000568 -3.2 1.1 -1.5 -0.8 -0.3     -0.4304152        -0.1366944

8.4.1.2 Gráficos

• Diagrama de cajas y bigotes

df %>% ggplot(aes(x = diferencia)) + 
  geom_boxplot(fill="#00BFC4")

8.4.2 Estudios inferenciales

8.4.2.1 Test de normalidad de Shapiro-Wilks

Objetivo: Comprobar la normalidad de la distribución de la diferencia.

Hipótesis nula: La distribución es normal.

Ejemplo: Comprobar la normalidad de la diferencia entre las notas de las asignaturas A y B de un mismo grupo de alumnos.

df %>% summarise(`Estadístico W` = shapiro.test(diferencia)$statistic, `p-valor` = shapiro.test(diferencia)$p.value)

  Estadístico W    p-valor
1     0.9794023 0.07367451

8.4.2.2 Test t de comparación de medias de dos poblaciones pareadas

Objetivo: Estimar la media de la diferencia o compararla con un valor dado μ₀.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con dos categorías (poblaciones) pareadas
• Distribución normal de la variable diferencia o tamaño muestral ≥ 30.

Hipótesis nula: La medias poblacionales son iguales (no existe una diferencia significativa entre las medias poblacionales).

Ejemplo: Comprobar si hay una diferencia signicativa entre las notas medias de las asinaturas A y B, o lo que es lo mismo, comprobar si la media de la diferencia de las notas de A y B es distinta de 0.

t.test (df$notaA, df$notaB, alternative = "two.sided", paired = TRUE)

    Paired t-test

data:  df$notaA and df$notaB
t = -10.506, df = 114, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -1.048005 -0.715473
sample estimates:
mean difference 
     -0.8817391 

• Diagrama de medias

df %>% ggplot(aes(x="", y = diferencia)) + 
  # Puntos de medias
  stat_summary(fun="mean", size=3,  geom="point") + 
  # Intervalos de confianza para la media
  stat_summary(fun.data = function(x) mean_cl_normal(x, conf.int=0.95), geom = "pointrange", position=position_dodge(width=0.25)) 

8.4.2.3 Test Wilcoxon de comparación de dos poblaciones pareadas (no paramétrico)

Objetivo: Comparar las medianas de las dos poblaciones.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con dos categorías (poblaciones) pareadas.

Hipótesis nula: La medianas poblacionales son iguales (no existe una diferencia significativa entre las medianas poblacionales).

Ejemplo: Comprobar si hay una diferencia signicativa entre las notas de las asignaturas A y B.

wilcox.test(df$notaA, df$notaB, alternative = "two.sided", paired = TRUE)

    Wilcoxon signed rank test with continuity correction

data:  df$notaA and df$notaB
V = 398, p-value = 2.442e-15
alternative hypothesis: true location shift is not equal to 0

8.5 Dos variables: Variable dependiente cuantitativa y variable independiente culitativa con más de dos categorías o grupos

8.5.1 Estudios descriptivos

8.5.1.1 Estadísticos

• Tamaño muestral de cada grupo
• Media de cada grupo
• Desviación típica de cada grupo
• Mínimo, Máximo de cada grupo
• Cuartiles de cada grupo
• Coeficiente de asimetría de cada grupo
• Coeficiente de apuntamiento de cada grupo

# Tamaño muestral de notaA según el grupo
df %>% group_by(grupo) %>% group_size()

[1] 38 35 47

# Media, Desviación típica, Mín, Máx, Cuartiles, Coef. Asimetría y Coef. Apuntamiento
library(moments)
df %>% group_by(grupo) %>% summarize(Media = mean(notaA, na.rm=TRUE), Des.Tip = sd(notaA, na.rm = TRUE), Mín = min(notaA, na.rm = TRUE), Máx = max(notaA, na.rm = TRUE), C1 = quantile(notaA, 0.25, na.rm = TRUE), C2 = quantile(notaA, 0.5, na.rm = TRUE), C3 = quantile(notaA, 0.75, na.rm = TRUE), Coef.Asimetría = skewness(notaA, na.rm = TRUE), Coef.Apuntamiento = kurtosis(notaA, na.rm = TRUE) - 3)

# A tibble: 3 × 10
  grupo Media Des.Tip   Mín   Máx    C1    C2    C3 Coef.Asimetría Coef.Apunta…¹
  <chr> <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>          <dbl>         <dbl>
1 A      6.54   0.998   4.3   8.6  5.93   6.6  7.15         -0.250        -0.166
2 B      6.96   1.23    3.5   9.3  6.2    6.8  7.7          -0.141         0.522
3 C      4.92   0.771   2.5   5.9  4.5    5.1  5.5          -1.06          0.902
# … with abbreviated variable name ¹​Coef.Apuntamiento

8.5.1.2 Gráficos

• Diagrama de cajas y bigotes

df %>% ggplot(aes(x = grupo, y = notaA, fill = grupo)) + 
  geom_boxplot() +
  # Cambio de escala del eje X
  scale_y_continuous(limits=c(0, 10), breaks = 0:10)

• Diagrama de violín

df %>% ggplot(aes(x = grupo, y = notaA, fill = grupo)) + 
  geom_violin() +
  # Cambio de escala del eje X
  scale_y_continuous(limits=c(0, 10), breaks = 0:10)

8.5.2 Estudios inferenciales

8.5.2.1 Test de normalidad de Shapiro-Wilks

Objetivo: Comprobar la normalidad de la distribución de cada población.

Hipótesis nula: La distribución es normal.

Ejemplo: Comprobar la normalidad de las distribuciones de la nota A en los grupos A, B y C.

df %>% group_by(grupo) %>% 
  summarise(`Estadístico W` = shapiro.test(notaA)$statistic, `p-valor` = shapiro.test(notaA)$p.value)

# A tibble: 3 × 3
  grupo `Estadístico W` `p-valor`
  <chr>           <dbl>     <dbl>
1 A               0.984   0.840  
2 B               0.963   0.277  
3 C               0.918   0.00280

Interpretación: La distribución de la nota A en los grupos A y B es normal (p-valores > 0.05) pero no en el grupo C (p-valor < 0.05)

Ejemplo: Comprobar la normalidad de las distribuciones de la nota C en los grupos A, B y C.

df %>% group_by(grupo) %>% 
  summarise(`Estadístico W` = shapiro.test(notaC)$statistic, `p-valor` = shapiro.test(notaC)$p.value)

# A tibble: 3 × 3
  grupo `Estadístico W` `p-valor`
  <chr>           <dbl>     <dbl>
1 A               0.989     0.961
2 B               0.965     0.343
3 C               0.976     0.442

Interpretación: La distribución de la nota C en los tres grupos es normal (p-valores > 0.05).

8.5.2.2 Test de Levene de comparación de varianzas de dos o más poblaciones independientes

Objetivo: Comparar las varianzas de dos o más poblaciones independientes.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con dos o más categorías (poblaciones)
• Distribución normal de la variable dependiente en todas las poblaciones o tamaños de las muestras de cada población ≥ 30.

Hipótesis nula: La varianzas poblacionales son iguales (no existe una diferencia significativa entre las medias poblacionales).

Ejemplo: Comprobar si diferencias signicativas entre las varianzas de las notas de la asignatura C de los grupos A, B y C.

# El test de Levene está disponible en el paquete car
library(car)
# Test de comparación de varianzas
leveneTest(notaC ~ grupo, data = df)

Levene's Test for Homogeneity of Variance (center = median)
       Df F value Pr(>F)
group   2  0.3186 0.7278
      116               

Interpretación: No existe diferencia significativa entre las varianzas de la nota C en los grupos A, B y C (p-valor > 0.05).

8.5.2.3 ANOVA de un factor para la comparación medias de más de dos poblaciones independientes

Objetivo: Comprobar si hay diferencias significativas entre las medias de más de dos poblaciones independientes.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con más de dos categorías (poblaciones)-
• Distribución normal de la variable dependiente en todas las poblaciones o tamaños de las muestras de cada población ≥ 30.
• Homogeneidad de varianzas en las poblaciones.

Hipótesis nula: La medias poblacionales son iguales (no existe una diferencia significativa entre las medias poblacionales).

Ejemplo: Comprobar si diferencias signicativas entre las notas medias de la asignatura C de los grupos A, B y C.

# Análisis de la varianza de un factor
summary(aov(notaC ~ grupo, data = df))

             Df Sum Sq Mean Sq F value   Pr(>F)    
grupo         2  80.69   40.34   20.05 3.32e-08 ***
Residuals   116 233.41    2.01                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1 observation deleted due to missingness

Interpretación: Existen diferencias significativas entre las medias de la nota C entre al menos dos grupos (p-valor=3.32e-08 < 0.05).

Observación: Cuando se detectan diferencias significativas entre las medias de al menos dos grupos conviene realizar un test de comparación múltiple por pares para ver entre qué poblaciones hay diferencias y entre cuáles no. Los test más habituales de comparación por pares son el de Tukey y el de Bonferroni.

# Test de comparación múltiple de Tukey
TukeyHSD(aov(notaC ~ grupo, data = df))

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = notaC ~ grupo, data = df)

$grupo
          diff        lwr        upr     p adj
B-A  0.4312693 -0.3637573  1.2262960 0.4048482
C-A -1.4455767 -2.1802858 -0.7108676 0.0000241
C-B -1.8768461 -2.6350758 -1.1186163 0.0000001

Interpretación: No existe una diferencia significativa entre las notas medias de la asignatura C de los grupos A y B (p-valor=0.4048 > 0.05), pero si existe una diferencia significativa entre las notas medias de los grupos A y C (p-valor=0.00002 < 0.05) y también entre las notas medias de los grupos B y C (p-valor=0.0000001 < 0.05).

• Diagrama de medias

df %>% ggplot(aes(x = grupo, y = notaC, colour = grupo)) + 
  # Puntos de medias
  stat_summary(fun="mean", size=3,  geom="point", position=position_dodge(width=0.25)) + 
  # Intervalos de confianza para la media
  stat_summary(fun.data = function(x) mean_cl_normal(x, conf.int=0.95), geom = "pointrange", position=position_dodge(width=0.25)) 

8.5.2.4 Test Kruskal-Wallis de comparación de más de dos poblaciones independientes (no paramétrico)

Objetivo: Comprobar si hay diferencias significativas entre entre más de dos poblaciones independientes.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cualitativa con más de dos categorías (poblaciones)

Hipótesis nula: La medianas poblacionales son iguales (no existe una diferencia significativa entre las medianas poblacionales).

Ejemplo: Comprobar si diferencias signicativas entre las notas de la asignatura A de los grupos A, B y C.

# Test de Kruskal-Wallis
kruskal.test(notaA ~ grupo, data = df)

    Kruskal-Wallis rank sum test

data:  notaA by grupo
Kruskal-Wallis chi-squared = 62.218, df = 2, p-value = 3.087e-14

Interpretación: Existen diferencias significativas entre las notas de la asignatura A de al menos dos de los grupos.

Observación: Cuando se detectan diferencias significativas entre al menos dos grupos conviene realizar un test de comparación múltiple por pares para ver entre qué poblaciones hay diferencias y entre cuáles no. El test más habitual es el de Wilcoxon.

# Test de comparación múltiple de Wilcoxon
pairwise.wilcox.test(df$notaA, df$grupo, p.adjust.method = "BH")

    Pairwise comparisons using Wilcoxon rank sum test with continuity correction 

data:  df$notaA and df$grupo 

  A       B      
B 0.19    -      
C 4.2e-10 1.3e-11

P value adjustment method: BH 

Interpretación: No existe una diferencia significativa entre las notas de la asignatura A de los grupos A y B (p-valor=0.19 > 0.05), pero si existe una diferencia significativa entre las notas de los grupos A y C (p-valor=4.2e-10 < 0.05) y también entre las notas de los grupos B y C (p-valor=1.3e-11 < 0.05).

8.6 Dos variables: Variable dependiente cuantitativa y variable independiente cuantitativa

8.6.1 Estudios descriptivos

8.6.1.1 Estadísticos

8.6.1.2 Estadísticos

• Tamaño muestral de cada grupo
• Media de cada variable
• Desviación típica de cada variable
• Mínimo, Máximo de cada variable
• Cuartiles de cada variable
• Coeficiente de asimetría de cada variable
• Coeficiente de apuntamiento de cada variable

# Tamaño muestral de notaA según el grupo
nrow(df)

[1] 120

# Media, Desviación típica, Mín, Máx, Cuartiles, Coef. Asimetría y Coef. Apuntamiento
library(moments)
df %>% summarize(Media = mean(notaA, na.rm=TRUE), Des.Tip = sd(notaA, na.rm = TRUE), Mín = min(notaA, na.rm = TRUE), Máx = max(notaA, na.rm = TRUE), C1 = quantile(notaA, 0.25, na.rm = TRUE), C2 = quantile(notaA, 0.5, na.rm = TRUE), C3 = quantile(notaA, 0.75, na.rm = TRUE), Coef.Asimetría = skewness(notaA, na.rm = TRUE), Coef.Apuntamiento = kurtosis(notaA, na.rm = TRUE) - 3)

     Media  Des.Tip Mín Máx  C1  C2    C3 Coef.Asimetría Coef.Apuntamiento
1 6.028333 1.340524 2.5 9.3 5.1 5.9 6.825      0.1373915         -0.102287

8.6.1.3 Gráficos

• Diagrama de dispersión

df %>% ggplot(aes(x = notaA, y = notaB)) + 
  geom_point()

8.6.2 Estudios inferenciales

8.6.2.1 Análisis de regresión

Objetivo: Construir un modelo matemático \(y=f(x)\) que explique lo mejor posible la variable dependiente en función de la independiente, para utilizarlo con fines predictivos.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cuantitativa.

Ejemplo: Construir el modelo lineal (recta de regresión) que mejor explica la relación entre la nota B y la nota A.

# Análisis de la varianza de un factor
lm(notaB ~ notaA, data = df)

Call:
lm(formula = notaB ~ notaA, data = df)

Coefficients:
(Intercept)        notaA  
     1.0224       0.9763  

# Análisis de la varianza de un factor
summary(lm(notaB ~ notaA, data = df))

Call:
lm(formula = notaB ~ notaA, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.99907 -0.59551 -0.07534  0.61398  2.31991 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.02243    0.40254    2.54   0.0124 *  
notaA        0.97628    0.06637   14.71   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9035 on 113 degrees of freedom
  (5 observations deleted due to missingness)
Multiple R-squared:  0.6569,    Adjusted R-squared:  0.6539 
F-statistic: 216.3 on 1 and 113 DF,  p-value: < 2.2e-16

Interpretación: La recta de regresión explica el 65% de la variabilidad de la nota B.

8.6.2.2 Análisis de correlación

Objetivo: Estudiar el grado de relación entre las dos variables.

Requisitos:

• Variable dependiente cuantitativa.
• Una variable independiente cuantitativa.

Hipótesis nula: Las dos variables son independientes.

Ejemplo: Ver si las notas A y B están relacionadas y cuál es su grado de relación.

# Análisis de la varianza de un factor
cor.test(df$notaA, df$notaB)

    Pearson's product-moment correlation

data:  df$notaA and df$notaB
t = 14.709, df = 113, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7367182 0.8651991
sample estimates:
      cor 
0.8104926 

Interpretación: Existe una correlación fuerte entre la nota A y la nota C, que además es estadísticamente muy significativa.

8.7 Ejercicios

1. El fichero genetica, contiene información de la análitica fisiológica, microbiológica y bioquímica, de una muestra de ratas tratadas con distintos tratamientos.

1. Crear un tibble con los datos del fichero.

Solución

library(tidyverse)
df <- read_csv('https://raw.githubusercontent.com/asalber/manual-r/master/datos/genetica.csv')
df

# A tibble: 21 × 20
   códig…¹ Trata…² mas c…³    IHS     IES     ITS    IAS gluco…⁴ pbmc(…⁵ CD4(c…⁶
   <chr>   <chr>     <dbl>  <dbl>   <dbl>   <dbl>  <dbl>   <dbl>   <dbl>   <dbl>
 1 Ct-A1   Control    236  0.0433 0.00198 0.00178 4.3e-4    54.1  7.01e3   401. 
 2 Ct-A2   Control    202. 0.044  0.002   0.0017  8  e-4    50.7  2.42e6   553. 
 3 Ct-B1   Control    246. 0.042  0.002   0.0015  5  e-4    72.2  6.19e6   724. 
 4 Ct-B2   Control    237. 0.0475 0.00238 0.00203 4.1e-4    95.3  1.79e6  2213. 
 5 Ct-B3   Control    231. 0.0499 0.002   0.0011  5  e-4    93.1  5.82e7  4518. 
 6 Ct-C1   Control    235. 0.05   0.0021  0.0033  1.4e-3    22.6  3.39e7   775. 
 7 Ct-C2   Control    228. 0.05   0.0018  0.0031  5.9e-4    29.4  7.5 e3    83.4
 8 Dx-1    Dexame…    181. 0.061  0.00155 0.0005  1.2e-4    56.0  7.68e2    10  
 9 Dx-2    Dexame…    198. 0.063  0.00191 0.0011  2  e-4   119.   1.41e6    15  
10 Dx-3    Dexame…    201. 0.0577 0.0017  0.0001  1  e-4   119.   7.12e3    11  
# … with 11 more rows, 10 more variables: `monoc(cel/mL)` <dbl>,
#   `IHQ: linfB(cel/mm2)` <dbl>, `pulp.blan(Tx1)` <dbl>,
#   `microorg(log nº/g)` <dbl>, `AI2(absorb)` <dbl>, `gluc(mmol/L)` <dbl>,
#   `TAG(mmol/L)` <dbl>, `col(mmol/L)` <dbl>, `HDL(mmol/L)` <dbl>,
#   `ins(pmol/L)` <dbl>, and abbreviated variable names ¹​`código muestra`,
#   ²​Tratamiento, ³​`mas cor (g)`, ⁴​`glucog(mg/g)`, ⁵​`pbmc(cel/mL)`,
#   ⁶​`CD4(cel/µL)`

2. Convertir el tratamiento en un factor.

Solución

df <- mutate(df, Tratamiento = factor(Tratamiento))

3. Calcular el tamaño muestral de cada grupo de tratamiento

Solución

count(df, Tratamiento)

# A tibble: 3 × 2
  Tratamiento      n
  <fct>        <int>
1 Control          7
2 Dexametasona     7
3 Kanamicina       7

4. Comprobar la normalidad de la variable IHS en cada grupo de tratamiento.

Solución

df %>% group_by(Tratamiento) %>% 
  summarise(`Estadístico W` = shapiro.test(IHS)$statistic, `p-valor` = shapiro.test(IHS)$p.value)

# A tibble: 3 × 3
  Tratamiento  `Estadístico W` `p-valor`
  <fct>                  <dbl>     <dbl>
1 Control                0.837    0.0928
2 Dexametasona           0.976    0.939 
3 Kanamicina             0.908    0.383 

5. Comprobar la homocedasticiad de varianzas de la variable IHS en los tres grupos de tratamiento.

Solución

# El test de Levene está disponible en el paquete car
library(car)
# Test de comparación de varianzas
leveneTest(IHS ~ Tratamiento, data = df)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2  0.1636 0.8503
      18               

6. Realizar un contraste de ANOVA para comparar las medias de la variable IHS entre los tres grupos de tratamiento.

Solución

# Análisis de la varianza de un factor
summary(aov(IHS ~ Tratamiento, data = df))

            Df    Sum Sq  Mean Sq F value   Pr(>F)    
Tratamiento  2 0.0007900 3.95e-04   31.78 1.24e-06 ***
Residuals   18 0.0002237 1.24e-05                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

7. Realizar los contrastes de comparación de medias de la variable IHS por pares de trataimentos.

Solución

# Test de comparación múltiple de Tukey
TukeyHSD(aov(IHS ~ Tratamiento, data = df))

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = IHS ~ Tratamiento, data = df)

$Tratamiento
                                 diff          lwr          upr     p adj
Dexametasona-Control     0.0133857143  0.008576441  0.018194988 0.0000037
Kanamicina-Control       0.0007857143 -0.004023559  0.005594988 0.9090945
Kanamicina-Dexametasona -0.0126000000 -0.017409273 -0.007790727 0.0000082

8. Realizar un contraste de Kruskal-Wallis para ver si hay diferencias significativas en la variable IHS entre los tres grupos de tratamiento.

Solución

# Test de Kruskal-Wallis
kruskal.test(IHS ~ Tratamiento, data = df)

    Kruskal-Wallis rank sum test

data:  IHS by Tratamiento
Kruskal-Wallis chi-squared = 13.433, df = 2, p-value = 0.001211

1. Construir la recta de regresión del variable IHS sobre la variable IES.

Solución

# Test de Kruskal-Wallis
lm(IHS ~ IES, data = df)

Call:
lm(formula = IHS ~ IES, data = df)

Coefficients:
(Intercept)          IES  
    0.08266    -15.97510  

summary(lm(IHS ~ IES, data = df))

Call:
lm(formula = IHS ~ IES, data = df)

Residuals:
       Min         1Q     Median         3Q        Max 
-0.0099081 -0.0040654  0.0006222  0.0031102  0.0142492 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.08266    0.01470   5.625 2.01e-05 ***
IES         -15.97510    7.47347  -2.138   0.0458 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.006558 on 19 degrees of freedom
Multiple R-squared:  0.1939,    Adjusted R-squared:  0.1514 
F-statistic: 4.569 on 1 and 19 DF,  p-value: 0.04577